Question: [Maximum mark: 6]
Let A and B be two independent events such that P(A ∩ B′) = 0.16 and P(A′ ∩ B) = 0.36.
(a) Given that P(A ∩ B) = x , find the value of x .
(b) Find P(A′ | B′).
Answer/Explanation
Ans:
(a) METHOD 1
EITHER
one of P(A) = x + 0.16 OR P(B) = x+ 0.36
OR
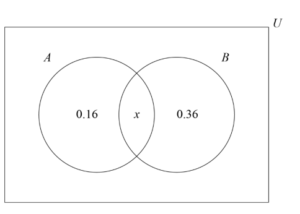
THEN
attempt to equate their P(A∩B) with their expression for P(A) × P (B)
P(A∩B) = P(A) × P (B) ⇒x=(x+0.16)×(x+0.36)
x = 0.24
METHOD 2
attempt to form at least one equation in P(A) and P(B) using independence
(P(A∩B’) = P(A) × P(B’) ⇒) P(A) × (1-P(B)) = 0.16 OR
(P(A’∩B) = P(A’) × P(B) ⇒) (1-P(A)) × P(B)) = 0.36
P(A) = 0.4 AND P(B) = 0.6
P(A∩B) = P(A) × P (B) =0.4×0.6
x = 0.24
(b) METHOD 1
recognising P( A’|B’ ) = P(A’)
= 1-0.16 – 0.24
=0.6

Question
Events \(A\) and \(B\) are such that \({\text{P}}(A) = 0.3\) and \({\text{P}}(B) = 0.4\) .
Find the value of \({\text{P}}(A \cup B)\) when
(i) \(A\) and \(B\) are mutually exclusive;
(ii) \(A\) and \(B\) are independent.
Given that \({\text{P}}(A \cup B) = 0.6\) , find \({\text{P}}(A|B)\) .
Answer/Explanation
Markscheme
(i) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) = 0.7\) A1
(ii) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\) (M1)
\( = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A){\text{P}}(B)\) (M1)
\( = 0.3 + 0.4 – 0.12 = 0.58\) A1
[4 marks]
\({\text{P}}(A \cap B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cup B)\)
\( = 0.3 + 0.4 – 0.6 = 0.1\) A1
\({\text{P}}(A|B) = \frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}}\) (M1)
\( = \frac{{0.1}}{{0.4}} = 0.25\) A1
[3 marks]
Examiners report
Most candidates attempted this question and answered it well. A few misconceptions were identified (eg \({\text{P}}(A \cup B) = {\text{P}}(A){\text{P}}(B)\) ). Many candidates were unsure about the meaning of independent events.
Most candidates attempted this question and answered it well. A few misconceptions were identified (eg \({\text{P}}(A \cup B) = {\text{P}}(A){\text{P}}(B)\) ). Many candidates were unsure about the meaning of independent events.
Question
Two events A and B are such that \({\text{P}}(A \cup B) = 0.7\) and \({\text{P}}(A|B’) = 0.6\).
Find \({\text{P}}(B)\).
Answer/Explanation
Markscheme
Note: Be aware that an unjustified assumption of independence will also lead to P(B) = 0.25, but is an invalid method.
METHOD 1
\({\text{P}}(A’|B’) = 1 – {\text{P}}(A|B’) = 1 – 0.6 = 0.4\) M1A1
\({\text{P}}(A’|B’) = \frac{{{\text{P}}(A’ \cap B’)}}{{{\text{P}}(B’)}}\)
\({\text{P}}(A’ \cap B’) = {\text{P}}\left( {(A \cup B)’} \right) = 1 – 0.7 = 0.3\) A1
\(0.4 = \frac{{0.3}}{{{\text{P}}(B’)}} \Rightarrow {\text{P(}}B’) = 0.75\) (M1)A1
\({\text{P}}(B) = 0.25\) A1
(this method can be illustrated using a tree diagram)
[6 marks]
METHOD 2
\({\text{P}}\left( {(A \cup B)’} \right) = 1 – 0.7 = 0.3\) A1
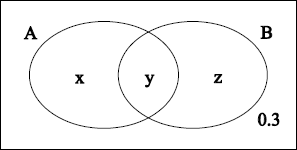
\({\text{P}}(A|B’) = \frac{x}{{x + 0.3}} = 0.6\) M1A1
\(x = 0.6x + 0.18\)
\(0.4x = 0.18\)
\(x = 0.45\) A1
\({\text{P}}(A \cup B) = x + y + z\)
\({\text{P}}(B) = y + z = 0.7 – 0.45\) (M1)
\( = 0.25\) A1
[6 marks]
METHOD 3
\(\frac{{{\text{P}}(A \cap B’)}}{{{\text{P}}(B’)}} = 0.6{\text{ (or P}}(A \cap B’) = 0.6{\text{P}}(B’)\) M1
\({\text{P}}(A \cap B’) = {\text{P}}(A \cup B) – {\text{P}}(B)\) M1A1
\({\text{P}}(B’) = 1 – {\text{P}}(B)\)
\(0.7 – {\text{P}}(B) = 0.6 – 0.6{\text{P}}(B)\) M1(A1)
\(0.1 = 0.4{\text{P}}(B)\)
\({\text{P}}(B) = \frac{1}{4}\) A1
[6 marks]
Examiners report
There is a great variety of ways to approach this question and there were plenty of very good solutions produced, all of which required an insight into the structure of conditional probability. A few candidates unfortunately assumed independence and so did not score well.
Question
Events \(A\) and \(B\) are such that \({\text{P}}(A) = \frac{2}{5},{\text{ P}}(B) = \frac{{11}}{{20}}\) and \({\text{P}}(A|B) = \frac{2}{{11}}\).
(a) Find \({\text{P}}(A \cap B)\).
(b) Find \({\text{P}}(A \cup B)\).
(c) State with a reason whether or not events \(A\) and \(B\) are independent.
Answer/Explanation
Markscheme
(a) \({\text{P}}(A \cap B) = {\text{P}}(A|B) \times P(B)\)
\({\text{P}}(A \cap B) = \frac{2}{{11}} \times \frac{{11}}{{20}}\) (M1)
\( = \frac{1}{{10}}\) A1
[2 marks]
(b) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\)
\({\text{P}}(A \cup B) = \frac{2}{5} + \frac{{11}}{{20}} – \frac{1}{{10}}\) (M1)
\( = \frac{{17}}{{20}}\) A1
[2 marks]
(c) No – events A and B are not independent A1
EITHER
\({\text{P}}(A|B) \ne {\text{P}}(A)\) R1
\(\left( {\frac{2}{{11}} \ne \frac{2}{5}} \right)\)
OR
\({\text{P}}(A) \times {\text{P}}(B) \ne {\text{P}}(A \cap B)\)
\(\frac{2}{5} \times \frac{{11}}{{20}} = \frac{{11}}{{50}} \ne \frac{1}{{10}}\) R1
Note: The numbers are required to gain R1 in the ‘OR’ method only.
Note: Do not award A1R0 in either method.
[2 marks]
Total [6 marks]
Examiners report
Question
A bag contains three balls numbered 1, 2 and 3 respectively. Bill selects one of these balls at random and he notes the number on the selected ball. He then tosses that number of fair coins.
Calculate the probability that no head is obtained.
Given that no head is obtained, find the probability that he tossed two coins.
Answer/Explanation
Markscheme
P(no heads from n coins tossed) = \({0.5^n}\) (A1)
P(no head) = \(\frac{1}{3} \times \frac{1}{2} + \frac{1}{3} \times \frac{1}{4} + \frac{1}{3} \times \frac{1}{8}\) M1
= \(\frac{7}{{24}}\) A1
[3 marks]
\({\text{P(2 | no heads)}} = \frac{{{\text{P(2 coins and no heads)}}}}{{{\text{P(no heads)}}}}\) M1
\( = \frac{{\frac{1}{{12}}}}{{\frac{7}{{24}}}}\) A1
\( = \frac{2}{7}\) A1
[3 marks]
Examiners report
[N/A]
[N/A]
