Question
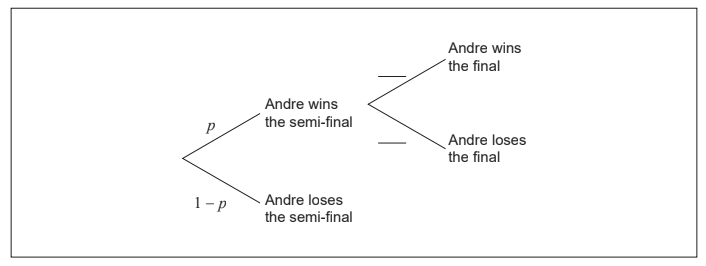
Andre will play in the semi-final of a tennis tournament.
If Andre wins the semi-final he will progress to the final. If Andre loses the semi-final,
he will not progress to the final.
If Andre wins the final, he will be the champion.
The probability that Andre will win the semi-final is p . If Andre wins the semi-final, then the
probability he will be the champion is 0.6.
Complete the values in the tree diagram. [1]
- b. The probability that Andre will not be the champion is 0.58.
- c. Find the value of p . [2]
- d. Given that Andre did not become the champion, find the probability that he lost in the semi-final. [3]
Answer/Explanation
Ans:
(a)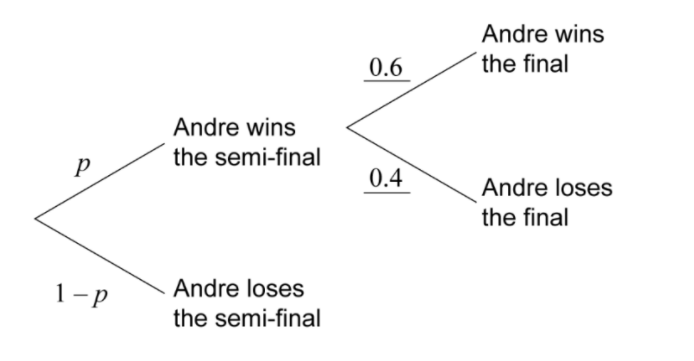 
(b)
p × 0.4+ (1-9)=0.58
OR
P × 0.6 = 1- 0.58
P= 0.7
(c)
\(\frac{0.3}{0.58}(\frac{1-0.7}{0.58})\)
OR
\(\frac{0.3}{0.3+0.7\times 0.4}\)
\(\frac{15}{29}\)(0.517,0.517241…,51.7%)
Question
In a class of 30 students, 19 play tennis, 3 play both tennis and volleyball, and 6 do not play either sport.
The following Venn diagram shows the events “plays tennis” and “plays volleyball”.
The values t and v represent numbers of students.
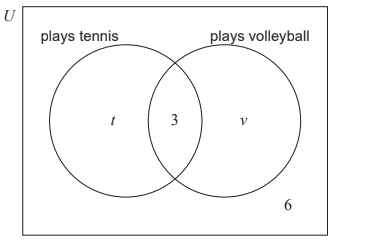
(i) Find the value of t .
(ii) Find the value of v . [4]
Find the probability that a randomly selected student from the class plays tennis or volleyball, but not both. [2]
Answer/Explanation
Ans:
(a)
(i)
valid approach to find t
eg t+ 3 = 19, 19 – 3
t =16 (may be seen on Venn diagram)
(ii)
valid approach to find v
eg t+ 3 + v + 6 = 30, 30- 19 – 6
v = 5 (may be seen on Venn diagram)
(b)
valid approach
eg 16+ 5 , 21 students, \(1-\frac{3+6}{30}\)
\(\frac{21}{30}(=\frac{7}{10})\)
Question
Two boxes contain numbered cards as shown below.
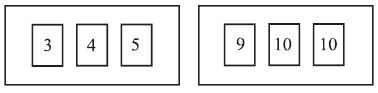
Two cards are drawn at random, one from each box.
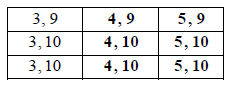
Copy and complete the table below to show all nine equally likely outcomes.
Let S be the sum of the numbers on the two cards.
Find the probability of each value of S.
Find the expected value of S.
Anna plays a game where she wins \(\$ 50\) if S is even and loses \(\$ 30\) if S is odd.
Anna plays the game 36 times. Find the amount she expects to have at the end of the 36 games.
Answer/Explanation
Markscheme
A2 N2
[2 marks]
\({\rm{P}}(12) = \frac{1}{9}\) , \({\rm{P}}(13) = \frac{3}{9}\) , \({\rm{P}}(14) = \frac{3}{9}\) , \({\rm{P}}(15) = \frac{2}{9}\) A2 N2
[2 marks]
correct substitution into formula for \({\text{E}}(X)\) A1
e.g. \({\rm{E}}(S) = 12 \times \frac{1}{9} + 13 \times \frac{3}{9} + 14 \times \frac{3}{9} + 15 \times \frac{2}{9}\)
\({\rm{E}}(S) = \frac{{123}}{9}\) A2 N2
[3 marks]
METHOD 1
correct expression for expected gain E(A) for 1 game (A1)
e.g. \(\frac{4}{9} \times 50 – \frac{5}{9} \times 30\)
\({\rm{E}}(A) = \frac{{50}}{9}\)
amount at end = expected gain for 1 game \( \times 36\) (M1)
= 200 (dollars) A1 N2
METHOD 2
attempt to find expected number of wins and losses (M1)
e.g. \(\frac{4}{9} \times 36\) , \(\frac{5}{9} \times 36\)
attempt to find expected gain E(G) (M1)
e.g. \(16 \times 50 – 30 \times 20\)
\({\text{E}}(G) = 200\) (dollars) A1 N2
[3 marks]
Question
Consider the events A and B, where \({\rm{P}}(A) = 0.5\) , \({\rm{P}}(B) = 0.7\) and \({\rm{P}}(A \cap B) = 0.3\) .
The Venn diagram below shows the events A and B, and the probabilities p, q and r.
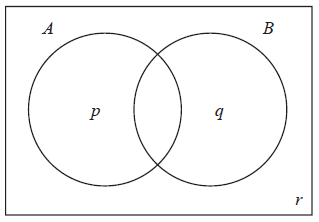
Write down the value of
(i) p ;
(ii) q ;
(iii) r.
Find the value of \({\rm{P}}(A|B’)\) .
Hence, or otherwise, show that the events A and B are not independent.
Answer/Explanation
Markscheme
(i) \(p = 0.2\) A1 N1
(ii) \(q = 0.4\) A1 N1
(iii) \(r = 0.1\) A1 N1
[3 marks]
\({\rm{P}}(A|B’) = \frac{2}{3}\) A2 N2
Note: Award A1 for an unfinished answer such as \(\frac{{0.2}}{{0.3}}\) .
[2 marks]
valid reason R1
e.g. \(\frac{2}{3} \ne 0.5\) , \(0.35 \ne 0.3\)
thus, A and B are not independent AG N0
[1 mark]
Question
The diagram below shows the probabilities for events A and B , with \({\rm{P}}(A’) = p\) .
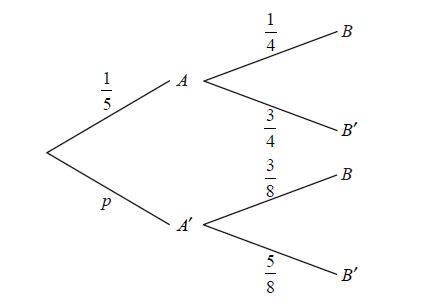
Write down the value of p .
Find \({\rm{P}}(B)\) .
Find \({\rm{P}}(A’|B)\) .
Answer/Explanation
Markscheme
\(p = \frac{4}{5}\) A1 N1
[1 mark]
multiplying along the branches (M1)
e.g. \(\frac{1}{5} \times \frac{1}{4}\) , \(\frac{{12}}{{40}}\)
adding products of probabilities of two mutually exclusive paths (M1)
e.g. \(\frac{1}{5} \times \frac{1}{4} + \frac{4}{5} \times \frac{3}{8}\) , \(\frac{1}{{20}} + \frac{{12}}{{40}}\)
\({\rm{P}}(B) = \frac{{14}}{{40}}\) \(\left( { = \frac{7}{{20}}} \right)\) A1 N2
[3 marks]
appropriate approach which must include \({A’}\) (may be seen on diagram) (M1)
e.g. \(\frac{{{\rm{P}}(A’ \cap B)}}{{{\rm{P}}(B)}}\) (do not accept \(\frac{{{\rm{P}}(A \cap B)}}{{{\rm{P}}(B)}}\) )
\({\rm{P}}(A’|B) = \frac{{\frac{4}{5} \times \frac{3}{8}}}{{\frac{7}{{20}}}}\) (A1)
\({\rm{P}}(A’|B) = \frac{{12}}{{14}}\) \(\left( { = \frac{6}{7}} \right)\) A1 N2
[3 marks]
Question
In a group of 16 students, 12 take art and 8 take music. One student takes neither art nor music. The Venn diagram below shows the events art and music. The values p , q , r and s represent numbers of students.
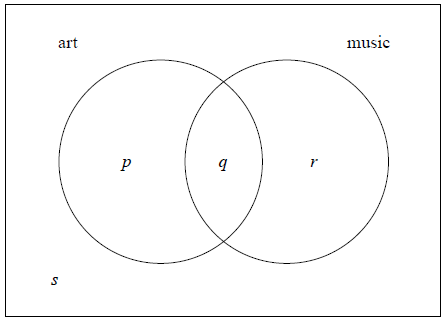
(i) Write down the value of s .
(ii) Find the value of q .
(iii) Write down the value of p and of r .
(i) A student is selected at random. Given that the student takes music, write down the probability the student takes art.
(ii) Hence, show that taking music and taking art are not independent events.
Two students are selected at random, one after the other. Find the probability that the first student takes only music and the second student takes only art.
Answer/Explanation
Markscheme
(i) \(s = 1\) A1 N1
(ii) evidence of appropriate approach (M1)
e.g. \(21 – 16\) , \(12 + 8 – q = 15\)
\(q = 5\) A1 N2
(iii) \(p = 7\) , \(r = 3\) A1A1 N2
[5 marks]
(i) \({\rm{P(art|music)}} = \frac{5}{8}\) A2 N2
(ii) METHOD 1
\({\rm{P(art)}} = \frac{{12}}{{16}}\) \(\left( { = \frac{3}{4}} \right)\) A1
evidence of correct reasoning R1
e.g. \(\frac{3}{4} \ne \frac{5}{8}\)
the events are not independent AG N0
METHOD 2
\({\rm{P(art)}} \times {\rm{P(music)}} = \frac{{96}}{{256}}\) \(\left( { = \frac{3}{8}} \right)\) A1
evidence of correct reasoning R1
e.g. \(\frac{{12}}{{16}} \times \frac{8}{{16}} \ne \frac{5}{{16}}\)
the events are not independent AG N0
[4 marks]
\({\text{P(first takes only music)}} = \frac{3}{{16}}\) (seen anywhere) A1
\({\text{P(second takes only art)}} = \frac{7}{{15}}\) (seen anywhere) A1
evidence of valid approach (M1)
e.g. \(\frac{3}{{16}} \times \frac{7}{{15}}\)
\({\text{P(music and art)}} = \frac{{21}}{{240}}\) \(\left( { = \frac{7}{{80}}} \right)\) A1 N2
[4 marks]
Question
The Venn diagram below shows events A and B where \({\rm{P}}(A) = 0.3\) , \({\rm{P}}(A \cup B) = 0.6\) and \({\rm{P}}(A \cap B) = 0.1\) . The values m , n , p and q are probabilities.
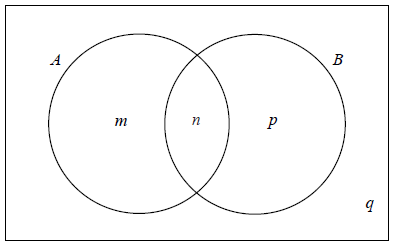
(i) Write down the value of n .
(ii) Find the value of m , of p , and of q .
Find \({\rm{P}}(B’)\) .
Answer/Explanation
Markscheme
(i) \(n = 0.1\) A1 N1
(ii) \(m = 0.2\) , \(p = 0.3\) , \(q = 0.4\) A1A1A1 N3
[4 marks]
appropriate approach
e.g. \({\rm{P}}(B’) = 1 – P(B)\) , \(m + q\) , \(1 – (n + p)\) (M1)
\({\rm{P}}(B’) = 0.6\) A1 N2
[2 marks]
Question
Events A and B are such that \({\rm{P}}(A) = 0.3\) , \({\rm{P}}(B) = 0.6\) and \({\rm{P}}(A \cup B) = 0.7\) .
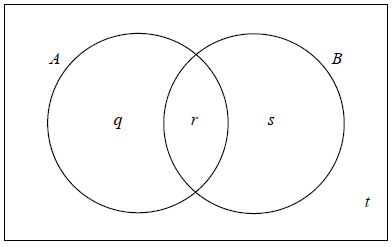
The values q , r , s and t represent probabilities.
Write down the value of t .
(i) Show that \(r = 0.2\) .
(ii) Write down the value of q and of s .
(i) Write down \({\rm{P}}(B’)\) .
(ii) Find \({\rm{P}}(A|B’)\) .
Answer/Explanation
Markscheme
\(t = 0.3\) A1 N1
[1 mark]
(i) correct values A1
e.g. \(0.3 + 0.6 – 0.7\) , \(0.9 – 0.7\)
\(r = 0.2\) AG N0
(ii) \(q = 0.1\) , \(s = 0.4\) A1A1 N2
[3 marks]
(i) \(0.4\) A1 N1
(ii) \({\rm{P}}(A|B’) = \frac{1}{4}\) A2 N2
[3 marks]
Question
Bag A contains three white balls and four red balls. Two balls are chosen at random without replacement.
(i) Copy and complete the following tree diagram.
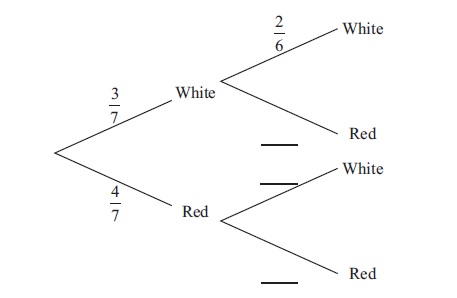
(ii) Find the probability that two white balls are chosen.
Bag A contains three white balls and four red balls. Two balls are chosen at random without replacement.
Bag B contains four white balls and three red balls. When two balls are chosen at random without replacement from bag B, the probability that they are both white is \(\frac{2}{7}\) .
A standard die is rolled. If 1 or 2 is obtained, two balls are chosen without replacement from bag A, otherwise they are chosen from bag B.
Find the probability that the two balls are white.
Bag A contains three white balls and four red balls. Two balls are chosen at random without replacement.
Bag B contains four white balls and three red balls. When two balls are chosen at random without replacement from bag B, the probability that they are both white is \(\frac{2}{7}\) .
A standard die is rolled. If 1 or 2 is obtained, two balls are chosen without replacement from bag A, otherwise they are chosen from bag B.
Given that both balls are white, find the probability that they were chosen from bag A.
Answer/Explanation
Markscheme
(i)
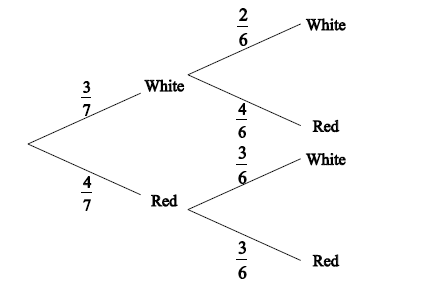
\(\frac{4}{6},\frac{3}{6}{\rm{and}}\frac{3}{6}\left( {\frac{2}{3},\frac{1}{2}{\rm{and}}\frac{1}{2}} \right)\) A1A1A1 N3
(ii) multiplying along the correct branches (may be seen on diagram) (A1)
e.g. \(\frac{3}{7} \times \frac{2}{6}\)
\(\frac{6}{{42}}\left( { = \frac{1}{7}} \right)\) A1 N2
[5 marks]
\({\rm{P(bag A) = }}\frac{2}{6}\left( { = \frac{1}{3}} \right)\) , \({\rm{P(bag B) = }}\frac{4}{6}\left( { = \frac{2}{3}} \right)\) (seen anywhere) (A1)(A1)
appropriate approach (M1)
e.g. \({\rm{P(}}WW \cap A) + {\rm{P}}(WW \cap B)\)
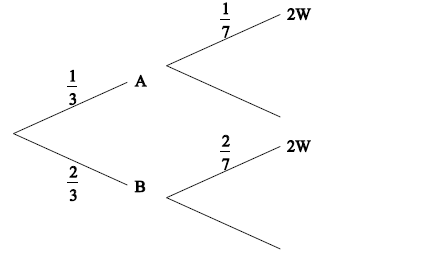
correct calculation A1
e.g. \(\frac{1}{3} \times \frac{1}{7} + \frac{2}{3} \times \frac{2}{7}\) , \(\frac{2}{{42}} + \frac{8}{{42}}\)
\({\rm{P}}(2W) = \frac{{60}}{{252}}\left( { = \frac{5}{{21}}} \right)\) A1 N3
[5 marks]
recognizing conditional probability (M1)
e.g. \(\frac{{{\rm{P}}(A \cap B)}}{{{\rm{P}}(B)}}\) , \({\rm{P}}(A|WW) = \frac{{{\rm{P}}(WW \cap A)}}{{{\rm{P}}(WW)}}\)
correct numerator (A1)
e.g. \({\rm{P}}(A \cap WW) = \frac{6}{{42}} \times \frac{2}{6},\frac{1}{{21}}\)
correct denominator (A1)
e.g. \(\frac{6}{{252}},\frac{5}{{21}}\)
probability \(\frac{{84}}{{420}}\left( { = \frac{1}{5}} \right)\) A1 N3
[4 marks]
Question
Bill and Andrea play two games of tennis. The probability that Bill wins the first game is \(\frac{4}{5}\).
If Bill wins the first game, the probability that he wins the second game is \(\frac{5}{6}\).
If Bill loses the first game, the probability that he wins the second game is \(\frac{2}{3}\).
Copy and complete the following tree diagram. (Do not write on this page.)
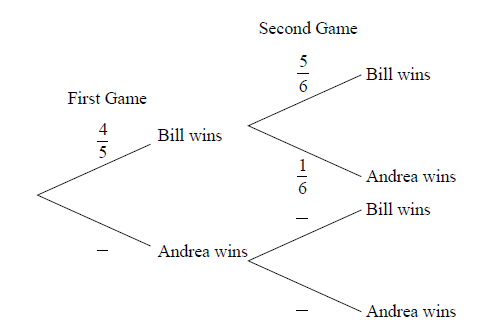
Find the probability that Bill wins the first game and Andrea wins the second game.
Find the probability that Bill wins at least one game.
Given that Bill wins at least one game, find the probability that he wins both games.
Answer/Explanation
Markscheme
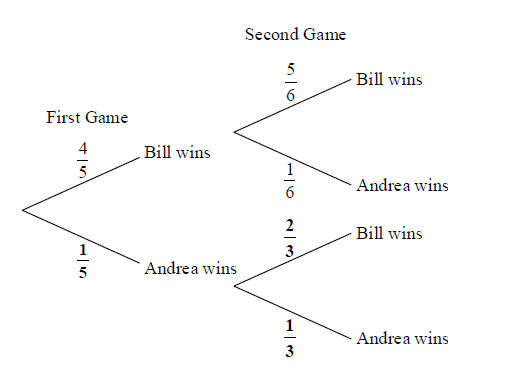A1A1A1 N3
Note: Award A1 for each correct bold probability.
[3 marks]
multiplying along the branches (may be seen on diagram) (M1)
eg \(\frac{4}{5} \times \frac{1}{6}\)
\(\frac{4}{{30}}\left( {\frac{2}{{15}}} \right)\) A1 N2
[2 marks]
METHOD 1
multiplying along the branches (may be seen on diagram) (M1)
eg \(\frac{4}{5} \times \frac{5}{6},{\text{ }}\frac{4}{5} \times \frac{1}{6},{\text{ }}\frac{1}{5} \times \frac{2}{3}\)
adding their probabilities of three mutually exclusive paths (M1)
eg \(\frac{4}{5} \times \frac{5}{6} + \frac{4}{5} \times \frac{1}{6} + \frac{1}{5} \times \frac{2}{3},{\text{ }}\frac{4}{5} + \frac{1}{5} \times \frac{2}{3}\)
correct simplification (A1)
eg \(\frac{{20}}{{30}} + \frac{4}{{30}} + \frac{2}{{15}},{\text{ }}\frac{2}{3} + \frac{2}{{15}} + \frac{2}{{15}}\)
\(\frac{{28}}{{30}}{\text{ }}\left( { = \frac{{14}}{{15}}} \right)\) A1 N3
METHOD 2
recognizing “Bill wins at least one” is complement of “Andrea wins 2” (R1)
eg finding P (Andrea wins 2)
P (Andrea wins both) \( = \frac{1}{5} \times \frac{1}{3}\) (A1)
evidence of complement (M1)
eg \(1 – p,{\text{ }}1 – \frac{1}{{15}}\)
\(\frac{{14}}{{15}}\) A1 N3
[4 marks]
P (B wins both) \(\frac{4}{5} \times \frac{5}{6}{\text{ }}\left( { = \frac{2}{3}} \right)\) A1
evidence of recognizing conditional probability (R1)
eg \({\text{P}}(A\left| B \right.),{\text{ P (Bill wins both}}\left| {{\text{Bill wins at least one), tree diagram}}} \right.\)
correct substitution (A2)
eg \(\frac{{\frac{4}{5} \times \frac{5}{6}}}{{\frac{{14}}{{15}}}}\)
\(\frac{{20}}{{28}}{\text{ }}\left( { = \frac{5}{7}} \right)\) A1 N3
[5 marks]
Question
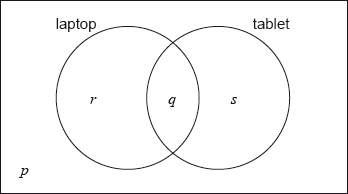
In a class of 21 students, 12 own a laptop, 10 own a tablet, and 3 own neither.
The following Venn diagram shows the events “own a laptop” and “own a tablet”.
The values \(p\), \(q\), \(r\) and \(s\) represent numbers of students.
A student is selected at random from the class.
Two students are randomly selected from the class. Let \(L\) be the event a “student owns a laptop”.
(i) Write down the value of \(p\).
(ii) Find the value of \(q\).
(iii) Write down the value of \(r\) and of \(s\).
(i) Write down the probability that this student owns a laptop.
(ii) Find the probability that this student owns a laptop or a tablet but not both.
(i) Copy and complete the following tree diagram. (Do not write on this page.)
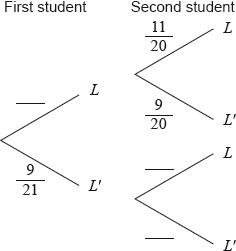
(ii) Write down the probability that the second student owns a laptop given that the first owns a laptop.
Answer/Explanation
Markscheme
(i) \(p = 3\) A1 N1
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)\((12 + 10 + 3) – 21,{\text{ }}22 – 18\)
\(q = 4\) A1 N2
(iii) \(r = 8,{\text{ }}s = 6\) A1A1 N2
(i) \(\frac{{12}}{{21}}{\text{ }}\left( { = \frac{4}{7}} \right)\) A2 N2
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)\(8 + 6,{\text{ }}r + s\)
\(\frac{{14}}{{21}}{\text{ }}\left( { = \frac{2}{3}} \right)\) A1 N2
(i) 
A1A1A1 N3
(ii) \(\frac{{11}}{{20}}\) A1 N1
[4 marks]
Question
In a group of 20 girls, 13 take history and 8 take economics. Three girls take both history and economics, as shown in the following Venn diagram. The values \(p\) and \(q\) represent numbers of girls.
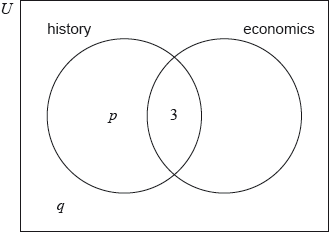
Find the value of \(p\);
Find the value of \(q\).
A girl is selected at random. Find the probability that she takes economics but not history.
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\(p + 3 = 13,{\text{ }}13 – 3\)
\(p = 10\) A1 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(p + 3 + 5 + q = 20,{\text{ }}10 – 10 – 8\)
\(q = 2\) A1 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(20 – p – q – 3,{\text{ }}1 – \frac{{15}}{{20}},{\text{ }}n(E \cap H’) = 5\)
\(\frac{5}{{20}}\,\,\,\left( {\frac{1}{4}} \right)\) A1 N2
[2 marks]
Question
A bag contains 5 green balls and 3 white balls. Two balls are selected at random without replacement.
Complete the following tree diagram.
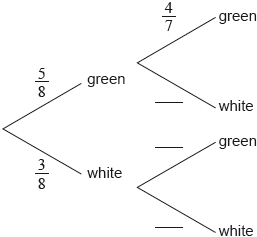
Find the probability that exactly one of the selected balls is green.
Answer/Explanation
Markscheme
correct probabilities
A1A1A1 N3
Note: Award A1 for each correct bold answer.
[3 marks]
multiplying along branches (M1)
eg\(\,\,\,\,\,\)\(\frac{5}{8} \times \frac{3}{7},{\text{ }}\frac{3}{8} \times \frac{5}{7},{\text{ }}\frac{{15}}{{56}}\)
adding probabilities of correct mutually exclusive paths (A1)
eg\(\,\,\,\,\,\)\(\frac{5}{8} \times \frac{3}{7} + \frac{3}{8} \times \frac{5}{7},{\text{ }}\frac{{15}}{{56}} + \frac{{15}}{{56}}\)
\(\frac{{30}}{{56}}{\text{ }}\left( { = \frac{{15}}{{28}}} \right)\) A1 N2
[3 marks]
Question
Pablo drives to work. The probability that he leaves home before 07:00 is \(\frac{3}{4}\).
If he leaves home before 07:00 the probability he will be late for work is \(\frac{1}{8}\).
If he leaves home at 07:00 or later the probability he will be late for work is \(\frac{5}{8}\).
Copy and complete the following tree diagram.
Find the probability that Pablo leaves home before 07:00 and is late for work.
Find the probability that Pablo is late for work.
Given that Pablo is late for work, find the probability that he left home before 07:00.
Two days next week Pablo will drive to work. Find the probability that he will be late at least once.
Answer/Explanation
Markscheme
A1A1A1 N3
Note: Award A1 for each bold fraction.
[3 marks]
multiplying along correct branches (A1)
eg \(\frac{3}{4} \times \frac{1}{8}\)
P(leaves before 07:00 ∩ late) = \(\frac{3}{32}\) A1 N2
[2 marks]
multiplying along other “late” branch (M1)
eg \(\frac{1}{4} \times \frac{5}{8}\)
adding probabilities of two mutually exclusive late paths (A1)
eg \(\left( {\frac{3}{4} \times \frac{1}{8}} \right) + \left( {\frac{1}{4} \times \frac{5}{8}} \right),\,\,\frac{3}{{32}} + \frac{5}{{32}}\)
\({\text{P}}\left( L \right) = \frac{8}{{32}}\,\,\left( { = \frac{1}{4}} \right)\) A1 N2
[3 marks]
recognizing conditional probability (seen anywhere) (M1)
eg \({\text{P}}\left( {A|B} \right),\,\,{\text{P}}\left( {{\text{before 7}}|{\text{late}}} \right)\)
correct substitution of their values into formula (A1)
eg \(\frac{{\frac{3}{{32}}}}{{\frac{1}{4}}}\)
\({\text{P}}\left( {{\text{left before 07:00}}|{\text{late}}} \right) = \frac{3}{8}\) A1 N2
[3 marks]
valid approach (M1)
eg 1 − P(not late twice), P(late once) + P(late twice)
correct working (A1)
eg \(1 – \left( {\frac{3}{4} \times \frac{3}{4}} \right),\,\,2 \times \frac{1}{4} \times \frac{3}{4} + \frac{1}{4} \times \frac{1}{4}\)
\(\frac{7}{{16}}\) A1 N2
[3 marks]
Question
A four-sided die has three blue faces and one red face. The die is rolled.
Let B be the event a blue face lands down, and R be the event a red face lands down.
Write down
(i) P(B);
(ii) P(R).
If the blue face lands down, the die is not rolled again. If the red face lands down, the die is rolled once again. This is represented by the following tree diagram, where p, s, t are probabilities.
Find the value of p, of s and of t.
Guiseppi plays a game where he rolls the die. If a blue face lands down, he scores 2 and is finished. If the red face lands down, he scores 1 and rolls one more time. Let X be the total score obtained.
(i) Show that \({\text{P}}(X = 3) = \frac{3}{{16}}\) .
(ii) Find \({\text{P}}(X = 2)\) .
(i) Construct a probability distribution table for X.
(ii) Calculate the expected value of X.
If the total score is 3, Guiseppi wins \(\$ 10\). If the total score is 2, Guiseppi gets nothing.
Guiseppi plays the game twice. Find the probability that he wins exactly \(\$ 10\).
Answer/Explanation
Markscheme
(i) P(B) \( = \frac{3}{4}\) A1 N1
(ii) P(R) \( = \frac{1}{4}\) A1 N1
[2 marks]
\(p = \frac{3}{4}\) A1 N1
\(s = \frac{1}{4}\), \(t = \frac{3}{4}\) A1 N1
[2 marks]
(i) \({\text{P}}(X = 3)\)
\( = {\text{P (getting 1 and 2)}} = \frac{1}{4} \times \frac{3}{4}\) A1
\( = \frac{3}{{16}}\) AG N0
(ii) \({\text{P}}(X = 2) = \frac{1}{4} \times \frac{1}{4} + \frac{3}{4}{\text{ }}\left( {{\text{or }}1 – \frac{3}{{16}}} \right)\) (A1)
\( = \frac{{13}}{{16}}\) A1 N2
[3 marks]
(i)
A2 N2
(ii) evidence of using \({\text{E}}(X) = \sum{x{\text{P}}(X = x)} \) (M1)
\({\text{E}}(X) = 2\left( {\frac{{13}}{{16}}} \right) + 3\left( {\frac{3}{{16}}} \right)\) (A1)
\( = \frac{{35}}{{16}}{\text{ }}\left( { = 2\frac{3}{{16}}} \right)\) A1 N2
[5 marks]
win \(\$ 10 \Rightarrow \) scores 3 one time, 2 other time (M1)
\({\text{P}}(3) \times {\text{P}}(2) = \frac{{13}}{{16}} \times \frac{3}{{16}}\) (seen anywhere) A1
evidence of recognising there are different ways of winning \(\$ 10\) (M1)
e.g. \({\text{P}}(3) \times {\text{P}}(2) + {\text{P}}(2) \times {\text{P}}(3)\) , \(2\left( {\frac{{13}}{{16}} \times \frac{3}{{16}}} \right)\) , \(\frac{{36}}{{256}} + \frac{3}{{256}} + \frac{{36}}{{256}} + \frac{3}{{256}}\)
\({\text{P(win }}\$ 10) = \frac{{78}}{{256}}{\text{ }}\left( { = \frac{{39}}{{128}}} \right)\) A1 N3
[4 marks]
Question
There are 20 students in a classroom. Each student plays only one sport. The table below gives their sport and gender.
One student is selected at random.
(i) Calculate the probability that the student is a male or is a tennis player.
(ii) Given that the student selected is female, calculate the probability that the student does not play football.
Two students are selected at random. Calculate the probability that neither student plays football.
Answer/Explanation
Markscheme
(i) correct calculation (A1)
e.g. \(\frac{9}{{20}} + \frac{5}{{20}} – \frac{2}{{20}}\) , \(\frac{{4 + 2 + 3 + 3}}{{20}}\)
\({\text{P(male or tennis)}} = \frac{{12}}{{20}}\) A1 N2
(ii) correct calculation (A1)
e.g. \(\frac{6}{{20}} \div \frac{{11}}{{20}}\) , \(\frac{{3 + 3}}{{11}}\)
\({\text{P(not football|female)}} = \frac{6}{{11}}\) A1 N2
[4 marks]
\({\text{P(first not football)}} = \frac{{11}}{{20}}\) , \({\text{P(second not football)}} = \frac{{10}}{{19}}\) A1
\({\text{P(neither football)}} = \frac{{11}}{{20}} \times \frac{{10}}{{19}}\) A1
\({\text{P(neither football)}} = \frac{{110}}{{380}}\) A1 N1
[3 marks]
Question
Let A and B be independent events, where \({\text{P}}(A) = 0.6\) and \({\text{P}}(B) = x\) .
Write down an expression for \({\text{P}}(A \cap B)\) .
Given that \({\text{P}}(A \cup B) = 0.8\) ,
(i) find x ;
(ii) find \({\text{P}}(A \cap B)\) .
Hence, explain why A and B are not mutually exclusive.
Answer/Explanation
Markscheme
\({\text{P}}(A \cap B) = {\text{P}}(A) \times {\text{P}}(B)( = 0.6x)\) A1 N1
[1 mark]
(i) evidence of using \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A){\text{P}}(B)\) (M1)
correct substitution A1
e.g. \(0.8 = 0.6 + x – 0.6x\) , \(0.2 = 0.4x\)
\(x = 0.5\) A1 N2
(ii) \({\text{P}}(A \cap B) = 0.3\) A1 N1
[4 marks]
valid reason, with reference to \({\text{P(}}A \cap B)\) R1 N1
e.g. \({\text{P(}}A \cap B) \ne 0\)
[1 mark]
Question
Consider the events A and B, where \({\rm{P}}(A) = 0.5\) , \({\rm{P}}(B) = 0.7\) and \({\rm{P}}(A \cap B) = 0.3\) .
The Venn diagram below shows the events A and B, and the probabilities p, q and r.
Write down the value of
(i) p ;
(ii) q ;
(iii) r.
Find the value of \({\rm{P}}(A|B’)\) .
Hence, or otherwise, show that the events A and B are not independent.
Answer/Explanation
Markscheme
(i) \(p = 0.2\) A1 N1
(ii) \(q = 0.4\) A1 N1
(iii) \(r = 0.1\) A1 N1
[3 marks]
\({\rm{P}}(A|B’) = \frac{2}{3}\) A2 N2
Note: Award A1 for an unfinished answer such as \(\frac{{0.2}}{{0.3}}\) .
[2 marks]
valid reason R1
e.g. \(\frac{2}{3} \ne 0.5\) , \(0.35 \ne 0.3\)
thus, A and B are not independent AG N0
[1 mark]
Question
José travels to school on a bus. On any day, the probability that José will miss the bus is \(\frac{1}{3}\) .
If he misses his bus, the probability that he will be late for school is \(\frac{7}{8}\) .
If he does not miss his bus, the probability that he will be late is \(\frac{3}{8}\) .
Let E be the event “he misses his bus” and F the event “he is late for school”.
The information above is shown on the following tree diagram.
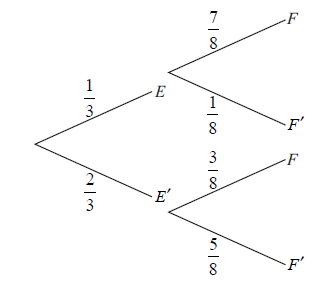
Find
(i) \({\rm{P}}(E \cap F)\) ;
(ii) \({\rm{P}}(F)\) .
Find the probability that
(i) José misses his bus and is not late for school;
(ii) José missed his bus, given that he is late for school.
The cost for each day that José catches the bus is 3 euros. José goes to school on Monday and Tuesday.
Copy and complete the probability distribution table.
The cost for each day that José catches the bus is 3 euros. José goes to school on Monday and Tuesday.
Find the expected cost for José for both days.
Answer/Explanation
Markscheme
(i) \(\frac{7}{{24}}\) A1 N1
(ii) evidence of multiplying along the branches (M1)
e.g. \(\frac{2}{3} \times \frac{5}{8}\) , \(\frac{1}{3} \times \frac{7}{8}\)
adding probabilities of two mutually exclusive paths (M1)
e.g. \(\left( {\frac{1}{3} \times \frac{7}{8}} \right) + \left( {\frac{2}{3} \times \frac{3}{8}} \right)\) , \(\left( {\frac{1}{3} \times \frac{1}{8}} \right) + \left( {\frac{2}{3} \times \frac{5}{8}} \right)\)
\({\rm{P}}(F) = \frac{{13}}{{24}}\) A1 N2
[4 marks]
(i) \(\frac{1}{3} \times \frac{1}{8}\) (A1)
\(\frac{1}{{24}}\) A1
(ii) recognizing this is \({\rm{P}}(E|F)\) (M1)
e.g. \(\frac{7}{{24}} \div \frac{{13}}{{24}}\)
\(\frac{{168}}{{312}}\) \(\left( { = \frac{7}{{13}}} \right)\) A2 N3
[5 marks]
A2A1 N3
[3 marks]
correct substitution into \({\rm{E}}(X)\) formula (M1)
e.g. \(0 \times \frac{1}{9} + 3 \times \frac{4}{9} + 6 \times \frac{4}{9}\) , \(\frac{{12}}{9} + \frac{{24}}{9}\)
\({\rm{E}}(X) = 4\) (euros) A1 N2
[2 marks]
Question
A box contains six red marbles and two blue marbles. Anna selects a marble from the box. She replaces the marble and then selects a second marble.
Write down the probability that the first marble Anna selects is red.
Find the probability that Anna selects two red marbles.
Find the probability that one marble is red and one marble is blue.
Answer/Explanation
Markscheme
Note: In this question, method marks may be awarded for selecting without replacement, as noted in the examples.
\({\rm{P}}(R) = \frac{6}{8}\left( { = \frac{3}{4}} \right)\) A1 N1
[1 mark]
attempt to find \({\rm{P(Red)}} \times {\rm{P(Red)}}\) (M1)
e.g. \({\rm{P(}}R{\rm{)}} \times {\rm{P(}}R{\rm{)}}\) , \(\frac{3}{4} \times \frac{3}{4}\) , \(\frac{6}{8} \times \frac{5}{7}\)
\({\rm{P}}(2R) = \frac{{36}}{{64}}\left( { = \frac{9}{{16}}} \right)\) A1 N2
[2 marks]
METHOD 1
attempt to find \({\rm{P(Red)}} \times {\rm{P(Blue)}}\) (M1)
e.g. \({\rm{P(}}R{\rm{)}} \times {\rm{P(}}B{\rm{)}}\) , \(\frac{6}{8} \times \frac{2}{8}\) , \(\frac{6}{8} \times \frac{2}{7}\)
recognizing two ways to get one red, one blue (M1)
e.g. \({\rm{P}}(RB) + {\rm{P}}(BR)\) , \(2\left( {\frac{{12}}{{64}}} \right)\) , \(\frac{6}{8} \times \frac{2}{7} + \frac{2}{8} \times \frac{6}{7}\)
\({\rm{P}}(1R,1B) = \frac{{24}}{{64}}\left( { = \frac{3}{8}} \right)\) A1 N2
[3 marks]
METHOD 2
recognizing that \({\rm{P}}(1R,1B)\) is \(1 – {\rm{P}}(2B) – {\rm{P}}(2R)\) (M1)
attempt to find \({\rm{P}}(2R)\) and \({\rm{P}}(2B)\) (M1)
e.g. \({\rm{P}}(2R) = \frac{3}{4} \times \frac{3}{4}\) , \(\frac{6}{8} \times \frac{5}{7}\) ; \({\rm{P}}(2B) = \frac{1}{4} \times \frac{1}{4}\) , \(\frac{2}{8} \times \frac{1}{7}\)
\({\rm{P}}(1R,1B) = \frac{{24}}{{64}}\left( { = \frac{3}{8}} \right)\) A1 N2
[3 marks]
Question
Celeste wishes to hire a taxicab from a company which has a large number of taxicabs.
The taxicabs are randomly assigned by the company.
The probability that a taxicab is yellow is 0.4.
The probability that a taxicab is a Fiat is 0.3.
The probability that a taxicab is yellow or a Fiat is 0.6.
Find the probability that the taxicab hired by Celeste is not a yellow Fiat.
Answer/Explanation
Markscheme
recognize need for intersection of Y and F (R1)
eg \({\text{P}}(Y \cap F){\text{, }}0.3 \times 0.4\)
valid approach to find \({\text{P}}(Y \cap F)\) (M1)
eg \({\text{P}}(Y) + {\text{P}}(F) – {\text{P}}(Y \cup F)\), Venn diagram
correct working (may be seen in Venn diagram) (A1)
eg \(0.4 + 0.3 – 0.6\)
\({\text{P}}(Y \cap F) = 0.1\) A1
recognize need for complement of \(Y \cap F\) (M1)
eg \(1 – {\text{P}}(Y \cap F){\text{, }}1 – 0.1\)
\({\text{P}}\left( {(Y \cap F)’} \right) = 0.9\) A1 N3
[6 marks]
Examiners report
Question
Adam travels to school by car (\(C\)) or by bicycle (\(B\)). On any particular day he is equally likely to travel by car or by bicycle.
The probability of being late (\(L\)) for school is \(\frac{1}{6}\) if he travels by car.
The probability of being late for school is \(\frac{1}{3}\) if he travels by bicycle.
This information is represented by the following tree diagram.
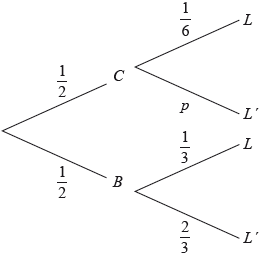
Find the value of \(p\).
Find the probability that Adam will travel by car and be late for school.
Find the probability that Adam will be late for school.
Given that Adam is late for school, find the probability that he travelled by car.
Adam will go to school three times next week.
Find the probability that Adam will be late exactly once.
Answer/Explanation
Markscheme
correct working (A1)
eg\(\;\;\;1 – \frac{1}{6}\)
\(p = \frac{5}{6}\) A1 N2
[2 marks]
multiplying along correct branches (A1)
eg\(\;\;\;\frac{1}{2} \times \frac{1}{6}\)
\({\text{P}}(C \cap L) = \frac{1}{{12}}\) A1 N2
[2 marks]
multiplying along the other branch (M1)
eg\(\;\;\;\frac{1}{2} \times \frac{1}{3}\)
adding probabilities of their \(2\) mutually exclusive paths (M1)
eg\(\;\;\;\frac{1}{2} \times \frac{1}{6} + \frac{1}{2} \times \frac{1}{3}\)
correct working (A1)
eg\(\;\;\;\frac{1}{{12}} + \frac{1}{6}\)
\({\text{P}}(L) = \frac{3}{{12}}\;\;\;\left( { = \frac{1}{4}} \right)\) A1 N3
[4 marks]
recognizing conditional probability (seen anywhere) (M1)
eg\(\;\;\;{\text{P}}(C|L)\)
correct substitution of their values into formula (A1)
eg\(\frac{{\frac{1}{{12}}}}{{\frac{3}{{12}}}}\)
\({\text{P}}(C|L) = \frac{1}{3}\) A1 N2
[3 marks]
valid approach (M1)
eg \(X \sim B\) \(\left({3,{\text{ }}\frac{1}{4}} \right),{\text{ }}\left({\frac{1}{4}} \right){\left({\frac{3}{4}} \right)^2},{\text{ }}\left( {\begin{array}{*{20}{c}}3 \\1\end{array}} \right)\), three ways it could happen
correct substitution (A1)
eg \(\;\;\;\left({\begin{array}{*{20}{c}}3\\1\end{array}}\right){\left({\frac{1}{4}}\right)^1}{\left({\frac{3}{4}} \right)^2},{\text{ }}\frac{1}{4}\times\frac{3}{4}\times\frac{3}{4} + \frac{3}{4} \times\frac{1}{4}\times\frac{3}{4} + \frac{3}{4}\times\frac{3}{4}\times\frac{1}{4}\)
correct working (A1)
eg\(\;\;\;3\left( {\frac{1}{4}} \right)\left( {\frac{9}{{16}}} \right),{\text{ }}\frac{9}{{64}} + \frac{9}{{64}} + \frac{9}{{64}}\)
\(\frac{{27}}{{64}}\) A1 N2
[4 marks]
Total [15 marks]
Question
Ann and Bob play a game where they each have an eight-sided die. Ann’s die has three green faces and five red faces; Bob’s die has four green faces and four red faces. They take turns rolling their own die and note what colour faces up. The first player to roll green wins. Ann rolls first. Part of a tree diagram of the game is shown below.
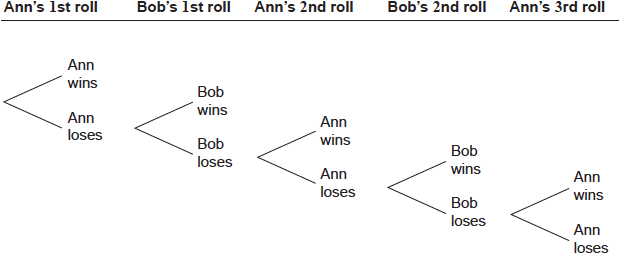
Find the probability that Ann wins on her first roll.
(i) The probability that Ann wins on her third roll is \(\frac{5}{8} \times \frac{4}{8} \times p \times q\ \times \frac{3}{8}\).
Write down the value of \(p\) and of \(q\).
(ii) The probability that Ann wins on her tenth roll is \(\frac{3}{8}{r^k}\) where \(r \in \mathbb{Q},{\text{ }}k \in \mathbb{Z}\).
Find the value of \(r\) and of \(k\).
Find the probability that Ann wins the game.
Answer/Explanation
Markscheme
recognizing Ann rolls green (M1)
eg\(\;\;\;{\text{P(G)}}\)
\(\frac{3}{8}\) A1 N2
[2 marks]
(i) \(p = \frac{4}{8},{\text{ }}q = \frac{5}{8}\) or \(q = \frac{4}{8},{\text{ }}p = \frac{5}{8}\) A1A1 N2
(ii) recognizes Ann and Bob lose \(9\) times (M1)
eg\(\;\;\;\(\overbrace {{A_L}{B_\(\overbrace {{A_L}{B_ \ldots \(\overbrace {{A_L}{B_{\text{ 9 times, }}\underbrace {\left( {\frac{5}{8} \times \frac{4}{8}} \right) \times \ldots \times \left( {\frac{5}{8} \times \frac{4}{8}} \right)}_{{\text{9 times}}}\)
\(k = 9\;\;\;\)(seen anywhere) A1 N2
correct working (A1)
eg\(\;\;\;{\left( {\frac{5}{8} \times \frac{4}{8}} \right)^9} \times \frac{3}{8},{\text{ }}\left( {\frac{5}{8} \times \frac{4}{8}} \right) \times \ldots \times \left( {\frac{5}{8} \times \frac{4}{8}} \right) \times \frac{3}{8}\)
\(r = \frac{{20}}{{64}}\;\;\;\left( { = \frac{5}{{16}}} \right)\) A1 N2
[6 marks]
recognize the probability is an infinite sum (M1)
eg\(\;\;\;\)Ann wins on her \({{\text{1}}^{{\text{st}}}}\) roll or \({{\text{2}}^{{\text{nd}}}}\) roll or \({{\text{3}}^{{\text{rd}}}}\) roll…, \({S_\infty }\)
recognizing GP (M1)
\({u_1} = \frac{3}{8}\;\;\;\)(seen anywhere) A1
\(r = \frac{{20}}{{64}}\;\;\;\)(seen anywhere) A1
correct substitution into infinite sum of GP A1
eg\(\;\;\;\frac{{\frac{3}{8}}}{{1 – \frac{5}{{16}}}},{\text{ }}\frac{3}{8}\left( {\frac{1}{{1 – \left( {\frac{5}{8} \times \frac{4}{8}} \right)}}} \right),{\text{ }}\frac{1}{{1 – \frac{5}{{16}}}}\)
correct working (A1)
eg\(\;\;\;\frac{{\frac{3}{8}}}{{\frac{{11}}{{16}}}},{\text{ }}\frac{3}{8} \times \frac{{16}}{{11}}\)
\({\text{P (Ann wins)}} = \frac{{48}}{{88}}\;\;\;\left( { = \frac{6}{{11}}} \right)\) A1 N1
[7 marks]
Total [15 marks]
Question
In a class of 100 boys, 55 boys play football and 75 boys play rugby. Each boy must play at least one sport from football and rugby.
(i) Find the number of boys who play both sports.
(ii) Write down the number of boys who play only rugby.
One boy is selected at random.
(i) Find the probability that he plays only one sport.
(ii) Given that the boy selected plays only one sport, find the probability that he plays rugby.
Let A be the event that a boy plays football and B be the event that a boy plays rugby.
Explain why A and B are not mutually exclusive.
Show that A and B are not independent.
Answer/Explanation
Markscheme
(i) evidence of substituting into \(n(A \cup B) = n(A) + n(B) – n(A \cap B)\) (M1)
e.g. \(75 + 55 – 100\) , Venn diagram
30 A1 N2
(ii) 45 A1 N1
[3 marks]
(i) METHOD 1
evidence of using complement, Venn diagram (M1)
e.g. \(1 – p\) , \(100 – 30\)
\(\frac{{70}}{{100}}\) \(\left( { = \frac{7}{{10}}} \right)\) A1 N2
METHOD 2
attempt to find P(only one sport) , Venn diagram (M1)
e.g. \(\frac{{25}}{{100}} + \frac{{45}}{{100}}\)
\(\frac{{70}}{{100}}\) \(\left( { = \frac{7}{{10}}} \right)\) A1 N2
(ii) \(\frac{{45}}{{70}}\) \(\left( { = \frac{9}{{14}}} \right)\) A2 N2
[4 marks]
valid reason in words or symbols (R1)
e.g. \({\rm{P}}(A \cap B) = 0\) if mutually exclusive, \({\rm{P}}(A \cap B) \ne 0\) if not mutually exclusive
correct statement in words or symbols A1 N2
e.g. \({\rm{P}}(A \cap B) = 0.3\) , \({\rm{P}}(A \cup B) \ne {\rm{P}}(A) + {\rm{P}}(B)\) , \({\rm{P}}(A) + {\rm{P}}(B) > 1\) , some students play both sports, sets intersect
[2 marks]
valid reason for independence (R1)
e.g. \({\rm{P}}(A \cap B) = {\rm{P}}(A) \times {\rm{P}}(B)\) , \({\rm{P}}(B|A) = {\rm{P}}(B)\)
correct substitution A1A1 N3
e.g. \(\frac{{30}}{{100}} \ne \frac{{75}}{{100}} \times \frac{{55}}{{100}}\) , \(\frac{{30}}{{55}} \ne \frac{{75}}{{100}}\)
[3 marks]
Question
The letters of the word PROBABILITY are written on 11 cards as shown below.
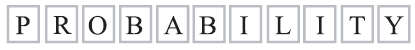
Two cards are drawn at random without replacement.
Let A be the event the first card drawn is the letter A.
Let B be the event the second card drawn is the letter B.
Find \({\rm{P}}(A)\) .
Find \({\rm{P}}(B|A)\) .
Find \({\rm{P}}(A \cap B)\) .
Answer/Explanation
Markscheme
\({\rm{P}}(A) = \frac{1}{{11}}\) A1 N1
[1 mark]
\({\rm{P}}(B|A) = \frac{2}{{10}}\) A2 N2
[2 marks]
recognising that \({\rm{P}}(A \cap B) = {\rm{P}}(A) \times {\rm{P}}(B|A)\) (M1)
correct values (A1)
e.g. \({\rm{P}}(A \cap B) = \frac{1}{{11}} \times \frac{2}{{10}}\)
\({\rm{P}}(A \cap B) = \frac{2}{{110}}\) A1 N3
[3 marks]
Question
Bag A contains three white balls and four red balls. Two balls are chosen at random without replacement.
(i) Copy and complete the following tree diagram.
(ii) Find the probability that two white balls are chosen.
Bag A contains three white balls and four red balls. Two balls are chosen at random without replacement.
Bag B contains four white balls and three red balls. When two balls are chosen at random without replacement from bag B, the probability that they are both white is \(\frac{2}{7}\) .
A standard die is rolled. If 1 or 2 is obtained, two balls are chosen without replacement from bag A, otherwise they are chosen from bag B.
Find the probability that the two balls are white.
Bag A contains three white balls and four red balls. Two balls are chosen at random without replacement.
Bag B contains four white balls and three red balls. When two balls are chosen at random without replacement from bag B, the probability that they are both white is \(\frac{2}{7}\) .
A standard die is rolled. If 1 or 2 is obtained, two balls are chosen without replacement from bag A, otherwise they are chosen from bag B.
Given that both balls are white, find the probability that they were chosen from bag A.
Answer/Explanation
Markscheme
(i)
\(\frac{4}{6},\frac{3}{6}{\rm{and}}\frac{3}{6}\left( {\frac{2}{3},\frac{1}{2}{\rm{and}}\frac{1}{2}} \right)\) A1A1A1 N3
(ii) multiplying along the correct branches (may be seen on diagram) (A1)
e.g. \(\frac{3}{7} \times \frac{2}{6}\)
\(\frac{6}{{42}}\left( { = \frac{1}{7}} \right)\) A1 N2
[5 marks]
\({\rm{P(bag A) = }}\frac{2}{6}\left( { = \frac{1}{3}} \right)\) , \({\rm{P(bag B) = }}\frac{4}{6}\left( { = \frac{2}{3}} \right)\) (seen anywhere) (A1)(A1)
appropriate approach (M1)
e.g. \({\rm{P(}}WW \cap A) + {\rm{P}}(WW \cap B)\)
correct calculation A1
e.g. \(\frac{1}{3} \times \frac{1}{7} + \frac{2}{3} \times \frac{2}{7}\) , \(\frac{2}{{42}} + \frac{8}{{42}}\)
\({\rm{P}}(2W) = \frac{{60}}{{252}}\left( { = \frac{5}{{21}}} \right)\) A1 N3
[5 marks]
recognizing conditional probability (M1)
e.g. \(\frac{{{\rm{P}}(A \cap B)}}{{{\rm{P}}(B)}}\) , \({\rm{P}}(A|WW) = \frac{{{\rm{P}}(WW \cap A)}}{{{\rm{P}}(WW)}}\)
correct numerator (A1)
e.g. \({\rm{P}}(A \cap WW) = \frac{6}{{42}} \times \frac{2}{6},\frac{1}{{21}}\)
correct denominator (A1)
e.g. \(\frac{6}{{252}},\frac{5}{{21}}\)
probability \(\frac{{84}}{{420}}\left( { = \frac{1}{5}} \right)\) A1 N3
[4 marks]
Question
Jar A contains three red marbles and five green marbles. Two marbles are drawn from the jar, one after the other, without replacement.
Jar B contains six red marbles and two green marbles. A fair six-sided die is tossed. If the score is \(1\) or \(2\), a marble is drawn from jar A. Otherwise, a marble is drawn from jar B.
Find the probability that
(i) none of the marbles are green;
(ii) exactly one marble is green.
Find the expected number of green marbles drawn from the jar.
(i) Write down the probability that the marble is drawn from jar B.
(ii) Given that the marble was drawn from jar B, write down the probability that it is red.
Given that the marble is red, find the probability that it was drawn from jar A.
Answer/Explanation
Markscheme
(i) attempt to find \({\rm{P(red)}} \times {\rm{P(red)}}\) (M1)
eg \(\frac{3}{8} \times \frac{2}{7}\) , \(\frac{3}{8} \times \frac{3}{8}\) , \(\frac{3}{8} \times \frac{2}{8}\)
\({\text{P(none green)}} = \frac{6}{{56}}\) \(\left( { = \frac{3}{{28}}} \right)\) A1 N2
(ii) attempt to find \({\rm{P(red)}} \times {\rm{P(green)}}\) (M1)
eg \(\frac{5}{8} \times \frac{3}{7}\) , \(\frac{3}{8} \times \frac{5}{8}\) , \(\frac{{15}}{{56}}\)
recognizing two ways to get one red, one green (M1)
eg \(2{\rm{P}}(R) \times {\rm{P}}(G)\) , \(\frac{5}{8} \times \frac{3}{7} + \frac{3}{8} \times \frac{5}{7}\) , \(\frac{3}{8} \times \frac{5}{8} \times 2\)
\({\text{P(exactly one green)}} = \frac{{30}}{{56}}\) \(\left( { = \frac{{15}}{{28}}} \right)\) A1 N2
[5 marks]
\({\text{P(both green)}} = \frac{{20}}{{56}}\) (seen anywhere) (A1)
correct substitution into formula for \({\rm{E}}(X)\) A1
eg \(0 \times \frac{6}{{56}} + 1 \times \frac{{30}}{{56}} + 2 \times \frac{{20}}{{56}}\) , \(\frac{{30}}{{64}} + \frac{{50}}{{64}}\)
expected number of green marbles is \(\frac{{70}}{{56}}\) \(\left( { = \frac{5}{4}} \right)\) A1 N2
[3 marks]
(i) \({\text{P(jar B)}} = \frac{4}{6}\) \(\left( { = \frac{2}{3}} \right)\) A1 N1
(ii) \({\text{P(red| jar B)}} = \frac{6}{8}\) \(\left( { = \frac{3}{4}} \right)\) A1 N1
[2 marks]
recognizing conditional probability (M1)
eg \({\rm{P}}(A|R)\) , \(\frac{{{\text{P(jar A and red)}}}}{{{\rm{P(red)}}}}\) , tree diagram
attempt to multiply along either branch (may be seen on diagram) (M1)
eg \({\text{P(jar A and red)}} = \frac{1}{3} \times \frac{3}{8}\) \(\left( { = \frac{1}{8}} \right)\)
attempt to multiply along other branch (M1)
eg \({\text{P(jar B and red)}} = \frac{2}{3} \times \frac{6}{8}\) \(\left( { = \frac{1}{2}} \right)\)
adding the probabilities of two mutually exclusive paths (A1)
eg \({\rm{P(red)}} = \frac{1}{3} \times \frac{3}{8} + \frac{2}{3} \times \frac{6}{8}\)
correct substitution
eg \({\text{P(jar A|red)}} = \frac{{\frac{1}{3} \times \frac{3}{8}}}{{\frac{1}{3} \times \frac{3}{8} + \frac{2}{3} \times \frac{6}{8}}}\) , \(\frac{{\frac{1}{8}}}{{\frac{5}{8}}}\) A1
\({\text{P(jar A|red)}} = \frac{1}{5}\) A1 N3
[6 marks]
Question
Two standard six-sided dice are tossed. A diagram representing the sample space is shown below.
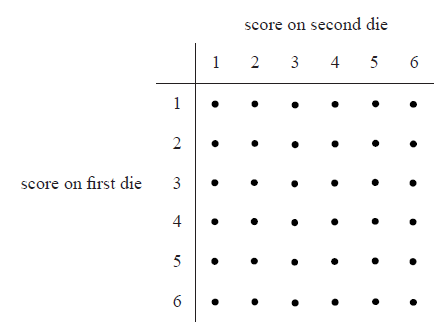
Let \(X\) be the sum of the scores on the two dice.
(i) Find \({\rm{P}}(X = 6)\) .
(ii) Find \({\rm{P}}(X > 6)\) .
(iii) Find \({\rm{P}}(X = 7|X > 6)\) .
Elena plays a game where she tosses two dice.
If the sum is 6, she wins 3 points.
If the sum is greater than 6, she wins 1 point.
If the sum is less than 6, she loses k points.
Find the value of k for which the game is fair.
Answer/Explanation
Markscheme
(i) number of ways of getting \(X = 6\) is 5 A1
\({\rm{P}}(X = 6) = \frac{5}{{36}}\) A1 N2
(ii) number of ways of getting \(X > 6\) is 21 A1
\({\rm{P}}(X > 6) = \frac{{21}}{{36}}\left( { = \frac{7}{{12}}} \right)\) A1 N2
(iii) \({\rm{P}}(X = 7|X > 6) = \frac{6}{{21}}\left( { = \frac{2}{7}} \right)\) A2 N2
[6 marks]
attempt to find \({\rm{P}}(X < 6)\) M1
e.g. \(1 – \frac{5}{{36}} – \frac{{21}}{{36}}\)
\({\rm{P}}(X < 6) = \frac{{10}}{{36}}\) A1
fair game if \({\rm{E}}(W) = 0\) (may be seen anywhere) R1
attempt to substitute into \({\rm{E}}(X)\) formula M1
e.g. \(3\left( {\frac{5}{{36}}} \right) + 1\left( {\frac{{21}}{{36}}} \right) – k\left( {\frac{{10}}{{36}}} \right)\)
correct substitution into \({\rm{E}}(W) = 0\) A1
e.g. \(3\left( {\frac{5}{{36}}} \right) + 1\left( {\frac{{21}}{{36}}} \right) – k\left( {\frac{{10}}{{36}}} \right) = 0\)
work towards solving M1
e.g. \(15 + 21 – 10k = 0\)
\(36 = 10k\) A1
\(k = \frac{{36}}{{10}}( = 3.6)\) A1 N4
[8 marks]
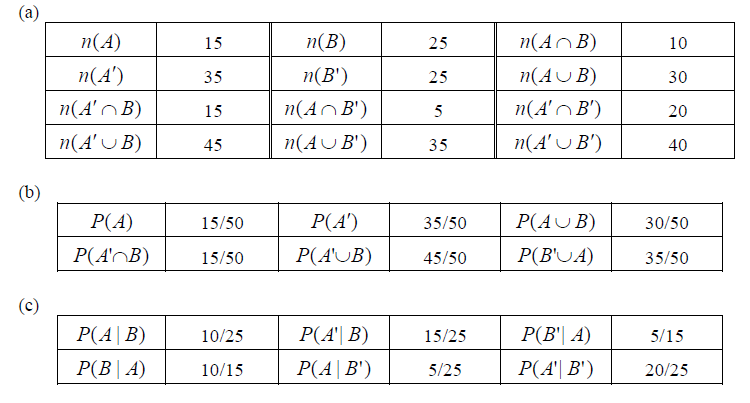
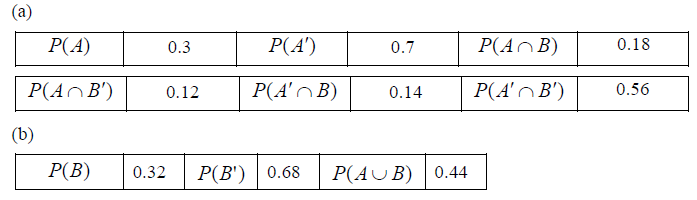
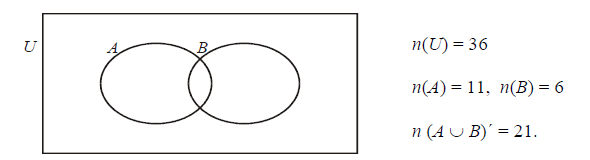
Question
The following Venn diagram shows the sample space U and the event A and B together with the numbers of elements in the corresponding regions. [Maximum mark: 18] [without GDC]
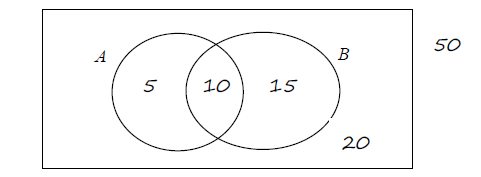
(a) Complete the following table.
(b) Write down the following probabilities
(c) Write down the following conditional probabilities
Answer/Explanation
Ans.
Question
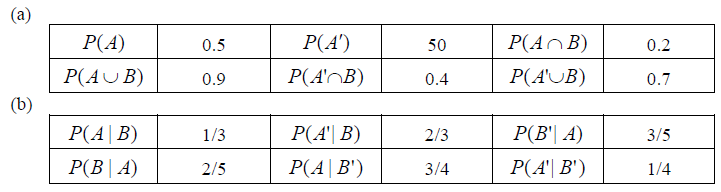
The following Venn diagram shows the sample space U and the events A and B together with their probabilities in the corresponding regions. [Maximum mark: 12] [without GDC]
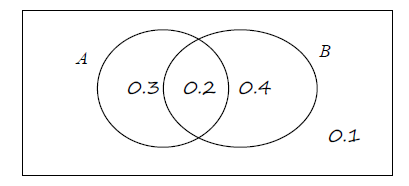
Answer/Explanation
Ans.
Question
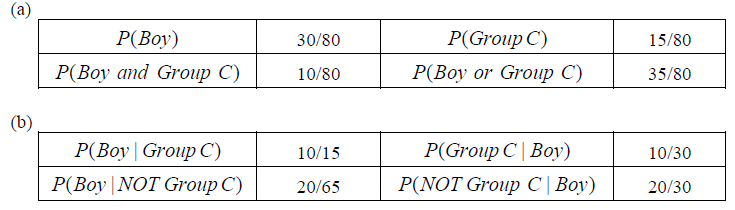
The following table shows the distribution of a population according to two criteria, gender and group. We select a person at random. [Maximum mark: 8] [without GDC]
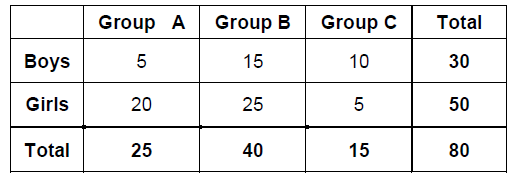
Answer/Explanation
Ans.
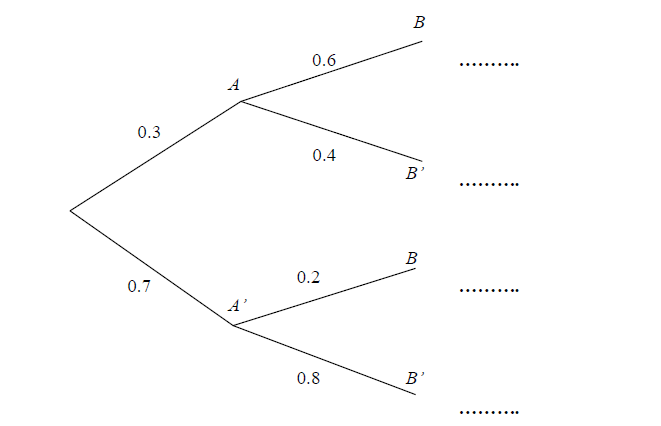
Question
In the following diagram complete the probabilities of the four different scenarios [Maximum mark: 10] [without GDC]
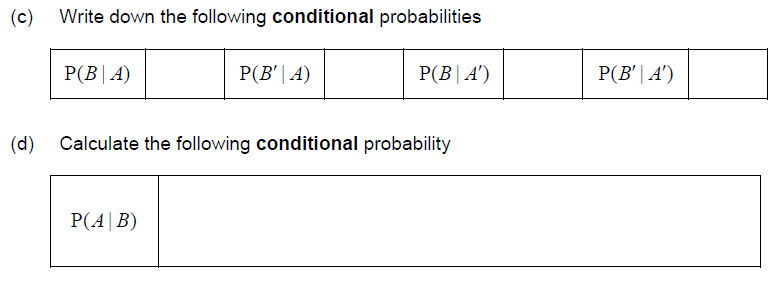
Answer/Explanation
Ans.
The four scenarios have probabilities 0.18, 0.12, 0.14, 0.56
Question
The following Venn diagram shows the sample space U and the events A and B together with their probabilities in the corresponding regions. [Maximum mark: 12] [without GDC]
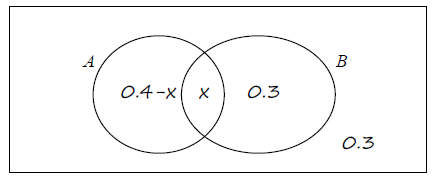
(a) Write down the values of P(A) and P(A∪B)
(b) Write down the value of \(x\) given that A and B are mutually exclusive.
(c) Find the value of \(x\) given that A and B are independent.
(d) Find the value of \(x\) given that P(A | B) = 0.5.
(e) Find the value of \(x\) given that P(B | A) = 0.25.
Answer/Explanation
Ans.
(a) P(A) = 0.4 P(A ∪ B) = 0.7 (b) x = 0. (c) x = 0.2 (d) x = 0.3 (e) x = 0.1
Question
The following Venn diagram shows the universal set U and the sets A and B . [Maximum mark: 4] [without GDC]
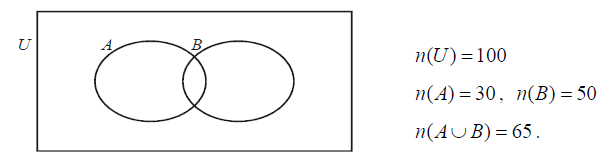
(a) Shade the area in the diagram which represents the set B ∩ A′ .
(b) Find n(B ∩ A′)
(c) An element is selected at random from U . What is the probability that this
element is in P(B ∩ A′) ?
Answer/Explanation
Ans.
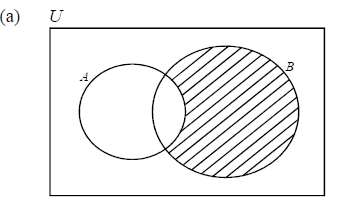
(b) \(n(A\cup B)=n(A)+n(B)-n(A\cap B)\Rightarrow 65=30+50-n(A\cap B)\)
\(\Rightarrow n(A\cap B)=15\) (may be on the diagram)
\(n(B\cap{A}’)=50-15=35\)
(c) \(P(B\cap {A}’)=\frac{35}{100}=0.35\)
Question
The following Venn diagram shows a sample space U and events A and B . [Maximum mark: 4] [without GDC]
(a) On the diagram, shade the region (A∪B)′ .
(b) Find (i) n( A ∩ B) ; (ii) P( A ∩ B)
(c) Explain why events A and B are not mutually exclusive.
Answer/Explanation
Ans.
(a)
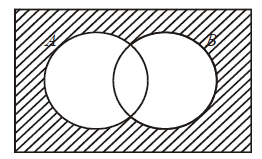
(b) (i) n(A ∩ B) = 2
(ii) P(A ∩ B) = \(\frac{2}{36}\left ( or\;\frac{1}{18} \right )\)
(c) n(A ∩ B) ≠ 0 (or equivalent)
Question
The Venn diagram below shows events A and B where P(A) = 0.3 , P(A ∪ B) = 0.6
and P(A∩B)= 0.1. The values \(m , n , p\) and \(q\) are probabilities. [Maximum mark: 6] [without GDC]
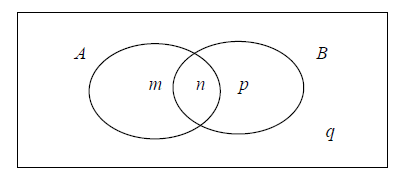
(a) (i) Write down the value of \(n\) .
(ii) Find the value of \(m\) , of \(p\) , and of \(q\) .
(b) Find P(B′) .
Answer/Explanation
Ans.
(a) (i) n = 0.1
(ii) m = 0.2, p = 0.3, q = 0.4
(b) P(B′) =1– P(B) = 0.6
Question
Consider the events A and B , where P(A) = 0.5 , P(B) = 0.7 and P(A∩B) = 0.3.
The Venn diagram below shows the events A and B , and the probabilities \(p , q , r \). [Maximum mark: 6] [without GDC]
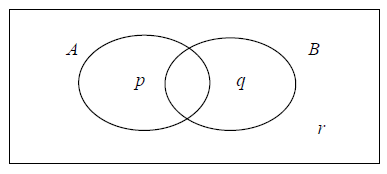
(a) Write down the value of (i) \(p\) ; (ii) \(q\) ; (iii) \(r\) .
(b) Find the value of P( A | B′) .
(c) Hence, or otherwise, show that the events A and B are not independent.
Answer/Explanation
Ans.
(a) (i) p = 0.2
(ii) q = 0.4
(iii) r = 0.1
(b) P(A│B′) = \(\frac{0.2}{0.3}=\frac{2}{3}\)
(c) P(A ∩ B) ≠ P(A)P(B) since 0.3 ≠ 0.35 OR P(A│B′) ≠ P(A) since \(\frac{2}{3}\)≠ 0.5
thus, A and B are not independent
Question
For the events A and B , P(A) = 0.6 , P(B) = 0.8 and P(A ∪ B) = 1.
(a) Find P(A ∩ B) ;
(b) Find P(A′∪ B′) [Maximum mark: 4] [without GDC]
Answer/Explanation
Ans.
(a) p(A ∩ B) = 0.6 + 0.8 – 1= 0.4
(b) p(A’ ∪ B‘) = 0.6
Question
The Venn diagram below shows information about 120 students in a school. Of these, 40 study Chinese (C), 35 study Japanese (J), and 30 study Spanish (S).
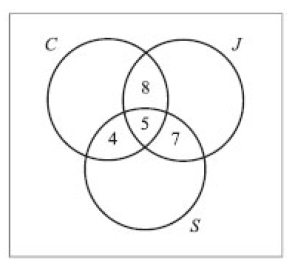
A student is chosen at random from the group. Find the probability that the student
(a) studies exactly two of these languages;
(b) studies only Japanese;
(c) does not study any of these languages. [Maximum mark: 6] [with GDC]
Answer/Explanation
Ans.
(a) \(\frac{19}{120}(=0.158)\)
(b) 35 – (8 + 5 + 7) = 15
Probability = \(\frac{15}{120}=\frac{1}{8}=0.125\)
(c) Number studying = 76
Number not studying = 120 – number studying = 44
Probability = \(\frac{44}{120}\left ( =\frac{11}{30}=0.367 \right )\)
Question
In a class, 40 students take chemistry only, 30 take physics only, 20 take both
chemistry and physics, and 60 take neither.
(a) Find the probability
(i) that a student takes physics given that the student takes chemistry.
(ii) that a student takes physics given that the student does not take chemistry.
(b) State whether the events “taking chemistry” and “taking physics” are mutually exclusive, independent, or neither. Justify your answer. [Maximum mark: 6] [without GDC]
Answer/Explanation
Ans.
(a) (i) P(P │C) =\(\frac{20}{20+40}=\frac{1}{3}\)
(ii) P(P │C′) = \(\frac{30}{30+60}=\frac{1}{3}\)
(b) P is independent of C
since P(P │C) = P(P) = 1/3 OR P(P)×P(C) = P(P ∩ C) = 2/15
Question
In a survey, 100 students were asked “do you prefer to watch television or play sport?” Of the 46 boys, 33 said they would choose sport, while 29 girls made this choice. [Maximum mark: 4] [without GDC]
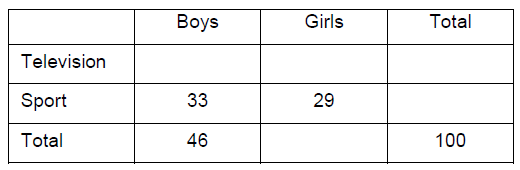
By completing this table or otherwise, find the probability that
(a) a student selected at random prefers to watch television;
(b) a student prefers to watch television, given that the student is a boy.
Answer/Explanation
Ans.
(a)
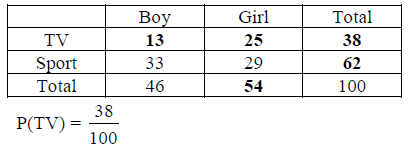
(b) P(TV │ Boy) = \(\frac{13}{46}\)
Question
In a survey of 200 people, 90 of whom were female, it was found that 60 people were
unemployed, including 20 males.
(a) Using this information, complete the table below.
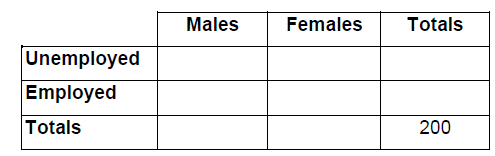
(b) If a person is selected at random from this group of 200, find the probability that
this person is
(i) an unemployed female;
(ii) a male, given that the person is employed. [Maximum mark: 4] [without GDC]
Answer/Explanation
Ans.
(a)
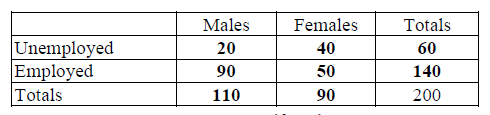
(b) (i) P(unemployed female) = \(\frac{40}{200}=\frac{1}{5}\)
(ii) P(male I employed person) = \(\frac{90}{140}=\frac{9}{14}\)
Question
The eye colour of 97 students is recorded in the chart below.
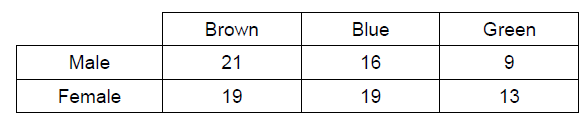
One student is selected at random. Write down
(a) the probability that the student is a male.
(b) the probability that the student has green eyes, given that the student is a female
(c) Find the probability that the student has green eyes or is male. [Maximum mark: 6] [without GDC]
Answer/Explanation
Ans.
(a) 46/97
(b) 13/51
(c) 59/97
Question
There are 20 students in a classroom. Each student plays only one sport. The table below gives their sport and gender.
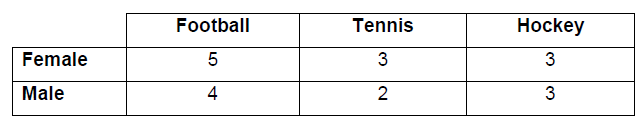
(a) One student is selected at random.
(i) Calculate the probability that the student is a male or is a tennis player.
(ii) Given that the student selected is female, calculate the probability that the
student does not play football.
(b) Two students are selected at random. Calculate the probability that neither student plays football. [Maximum mark: 7] [with GDC]
Answer/Explanation
Ans.
(a) (i) P(male or tennis) = \(\frac{12}{20}\left ( =\frac{3}{5} \right )\)
(ii) P(not football | female) =\(\frac{6}{11}\)
(b) P(neither football) = \(\frac{11}{20}x\frac{10}{19}=\frac{110}{380}\left ( =\frac{11}{38} \right )\)
Question
Consider events A, B such that P(A) ≠ 0, P(A) ≠1, P(B) ≠ 0 , and P(B) ≠ 1.
In each of the situations (i), (ii), (iii) below state whether A and B are
mutually exclusive (M); independent (I); neither (N).
(i) P(A| B) = P(A) (ii) P(A∩B) = 0 (iii) P(A∩B) = P(A) [Maximum mark: 6] [without GDC]
Answer/Explanation
Ans.
(i) Independent (I)
(ii) Mutually exclusive (M)
(iii) Neither (N)
Question
Consider the independent events A and B .
Given that P(B) = 2P(A) and P(A ∪ B)= 0.52 , find P(B) . [Maximum mark: 7] [with GDC]
Answer/Explanation
Ans.
Let P(A) = x, P(B) = 2x
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
P(A ∪ B) = P(A) + P(B) – P(A)( B)
0.52 = x + 2x – 2x2
x = 0.2, (1.3 rejected)
P(B) = 0.4
Question
The letters of the word PROBABILITY are written on 11 cards as shown below.
Two cards are drawn at random without replacement.
Let A be the event the first card drawn is the letter A.
Let B be the event the second card drawn is the letter B.
(a) Find P(A) .
(b) Find P(B | A) .
(c) Find P(A∩B) . [Maximum mark: 6] [without GDC]
Answer/Explanation
Ans.
(a) P(A) = \(\frac{1}{11}\)
(b) P(B │A) = \(\frac{2}{10}\)
(c) P(A ∩ B) = P(A) × P(B │A)
P(A ∩ B) =\(\frac{1}{11}x\frac{2}{10}=\frac{2}{110}\)
Question
The following diagram shows a circle divided into three sectors A, B and C. The angles at the centre of the circle are 90°,120° and 150°. Sectors A and B are shaded as shown The arrow is spun.
It cannot land on the lines between the sectors. Let A, B, C and S be the events defined by
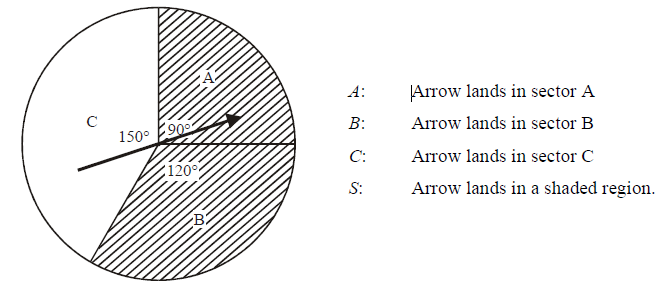
(a) Find P(B) ;
(b) Find P(S) ;
(c) Find P(A | S) . [Maximum mark: 6] [without GDC]
Answer/Explanation
Ans.
(a) \(\frac{120}{360}=\frac{1}{3}\)
(b) \(\frac{90+120}{360}=\frac{210}{360}=\frac{7}{12}\)
(c) \(\frac{90}{210}=\frac{3}{7}\)
Question
Let A and B be events such that P(A) = \(\frac{1}{2}\), P(B) = \(\frac{3}{4}\) and P(A∪ B) = \(\frac{7}{8}\)
(a) Calculate P(A∩B) .
(b) Calculate P(A | B) .
(c) Are the events A and B independent? Give a reason for your answer. [Maximum mark: 6] [without GDC]
Answer/Explanation
Ans.
(a) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
P(A ∩ B) = \(\frac{1}{2}+\frac{3}{4}-\frac{7}{8}=\frac{3}{8}\)
(b) P(A | B) = \(\frac{P(A\cap B)}{P(B)}\left ( =\frac{\frac{3}{8}}{\frac{3}{4}} \right )=\frac{1}{2}\)
(c) Yes, the events are independent
EITHER P(A | B) = P(A) OR P(A ∩ B) = P(A)P(B)
Question
Let A and B be independent events such that P(A) = 0.3 and P(B) = 0.8 .
(a) Find P(A ∩ B) .
(b) Find P(A∪ B) .
(c) Are A and B mutually exclusive? Justify your answer. [Maximum mark: 6] [without GDC]
Answer/Explanation
Ans.
(a) Independent ⇒ P(A ∩ B) = P(A) x P(B) = 0.3 x 0.8) = 0.24
(b) P(A ∪ B) = P(A) + P(B) – P(A ∩ B) = 0.3 + 0.8 – 0.24 = 0.86
(c) No since P(A ∩ B) ≠ 0 [OR P(A ∪ B) ≠ P(A) + P(B)]
Question
Events E and F are independent, with P(E) = \(\frac{2}{3}\) and P(E ∩ F) = \(\frac{1}{3}\) . Calculate
(a) P(F) ;
(b) P(E ∪ F) . [Maximum mark: 6] [without GDC]
Answer/Explanation
Ans.
(a) P(E ∩ F) = P(E)P(F)
\(\frac{1}{3}=\frac{2}{3}\)P(F),P(F)=\(\frac{\frac{1}{3}}{\frac{2}{3}}=\frac{1}{2}\)
(b) P(E ∪ F) = P(E) + P(F) – P(E ∩ F)
P(E ∪ F) = \(\frac{2}{3}+\frac{1}{2}-\frac{1}{3}=\frac{5}{6}\)
Question
Consider the events A and B , where P(A) =\(\frac{2}{5}\), P(B’ ) = \(\frac{1}{4}\) and P(A∪ B) =\(\frac{7}{8}\).
(a) Write down P(B) .
(b) Find P(A ∩ B) .
(c) Find P(A | B) . [Maximum mark: 6] [with GDC]
Answer/Explanation
Ans.
(a) \(\frac{3}{4}\)
(b) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
P(A ∩ B) = P(A) + P(B) – P(A ∪ B) = \(\frac{2}{5}+\frac{3}{4}-\frac{7}{8}=\frac{11}{40}\)
(c) P(A | B) = \(\frac{P(A\cap B)}{P(B)}\left ( =\frac{\frac{11}{40}}{\frac{3}{4}} \right )=\frac{11}{30}(0.367)\)
Question
Let A and B be independent events, where P(A) = 0.6 and P(B) = x .
(a) Write down an expression for P(A∩B) .
(b) Given that P(A∪ B) = 0.8 ,
(i) find x ; (ii) find P(A∩B) .
(c) Hence, explain why A and B are not mutually exclusive. [Maximum mark: 6] [without GDC]
Answer/Explanation
Ans.
(a) P(A ∩ B) = P(A) × P(B) = 0.6x
(b) (i) P(A ∪ B) = P(A) + P(B) – P(A)P(B)
0.80 = 0.6 + x – 0.6x ⇔ 0.2 = 0.4x ⇔ x = 0.5
(ii) P(A ∩ B) = 0.3
(c) P(A ∩ B) ≠ 0
Question
The events A and B are independent such that P(B) = 3P(A) and P(A∪ B) = 0.68 .
Find P(B) . [Maximum mark: 6] [with GDC]
Answer/Explanation
Ans.
Let P(A) = x then P(B) = 3x
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
0.68 = x + 3x – 3x2
3x2 – 4x + 0.68 = 0
x = 0.2 (x = 1.133, not possible)
P(B) = 3x = 0.6
Question
For events A and B , the probabilities are P(A) = \(\frac{3}{11}\), P(B) = \(\frac{4}{11}\) .
Calculate the value of P(A ∩ B)
(a) if P(A ∪ B) = \(\frac{6}{11}\);
(b) if events A and B are independent. [Maximum mark: 6] [with GDC]
Answer/Explanation
Ans.
(a) P (A ∪ B) = P (A) + P (B) – P (A ∩ B)
⇒ P (A ∩ B) = P (A) + P (B) – P (A ∪ B) =\(\frac{3}{11}+\frac{4}{11}-\frac{6}{11}=\frac{1}{11}\)
(b) P (A ∩ B) = P (A) × P (B) =\(\frac{3}{11}x\frac{4}{11}=\frac{12}{121}\)
Question
Two unbiased 6-sided dice are rolled, a red one and a black one. Let E and F be the
events
E : the same number appears on both dice;
F : the sum of the numbers is 10.
(a) Find P(E) .
(b) Find P(F) .
(c) Find P(E ∪ F) . [Maximum mark: 6] [without GDC]
Answer/Explanation
Ans.
Total number of possible outcomes = 36
(a) P(E) = P(1,1) + P(2, 2) + P(3, 3) + P(4, 4) + P(5, 5) + P(6, 6) = \(\frac{6}{36}\)
(b) P(F) = P(6, 4) + P(5, 5) + P(4, 6) = \(\frac{3}{36}\)
(c) P(E ∪ F) = P(E) + P(F) – P(E ∩ F)
P(E ∩ F) = \(\frac{1}{36}\)
P(E ∪ F) = \(\frac{6}{36}+\frac{3}{36}-\frac{1}{36}\left ( =\frac{8}{36}=\frac{2}{9},0.222\right )\)
Question
Two fair dice are thrown and the number showing on each is noted. The sum of these
two numbers is S. Find the probability that
(a) S is less than 8;
(b) at least one die shows a 3;
(c) at least one die shows a 3, given that S is less than 8. [Maximum mark: 7] [without GDC]
Answer/Explanation
Ans.
Sample space ={(1, 1), (1, 2) … (6, 5), (6, 6)} [a grid helps]
(a) P (S < 8) = \(\frac{6+5+4+3+2+1}{36}=\frac{7}{12} \) OR P (S < 8) = \(\frac{7}{12}\)
(b) P (at least one 3) = \(\frac{1+1+6+1+1+1}{36}=\frac{11}{36} \) OR directly = \(\frac{11}{36}\)
(c) P (at least one 3 | S < 8) = \(\frac{P(at\;least\;one\;3\cap S< 8)}{P(S<8)}=\frac{\frac{7}{36}}{\frac{7}{12}}=\frac{1}{3}\)
Question
Two ordinary, 6-sided dice are rolled and the total score is noted.
(a) Complete the tree diagram by entering probabilities and listing outcomes.
(b) Find the probability of getting one or more sixes. [Maximum mark: 4] [without GDC]
Answer/Explanation
Ans.
(a)
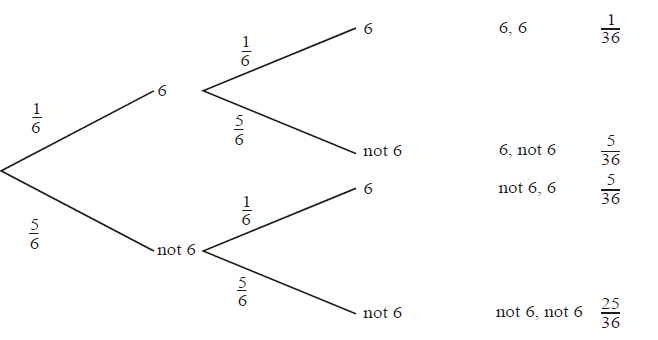
(b) P(one or more sixes) = \(\frac{1}{6}x\frac{1}{6}+\frac{1}{6}x\frac{5}{6}+\frac{5}{6}x\frac{1}{6}\) or \(\left ( 1-\frac{5}{6}x\frac{5}{6} \right )=\frac{11}{36}\)
Question
A bag contains four apples (A) and six bananas (B). A fruit is taken from the bag and eaten. Then a second fruit is taken and eaten.
(a) Complete the tree diagram below by writing probabilities in the spaces provided.
(b) Find the probability that one of each type of fruit was eaten. [Maximum mark: 6] [with GDC]
Answer/Explanation
Ans.
(a)
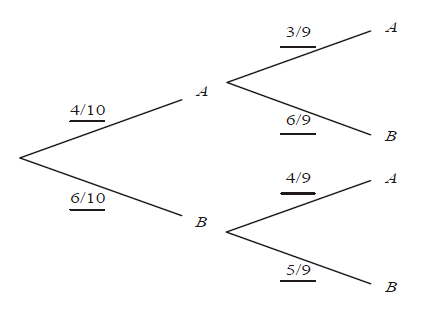
(b) \(\left ( \frac{4}{10}x\frac{6}{9} \right )+\left ( \frac{6}{10}x\frac{4}{9} \right )=\frac{48}{90}\left ( \frac{8}{15},0.533 \right )\)
Question
The events B and C are dependent, where C is the event “a student takes Chemistry”, and B is the event “a student takes Biology”. It is known that
P(C) = 0.4, P(B | C) = 0.6 , P(B | C′) = 0.5.
(a) Complete the following tree diagram.
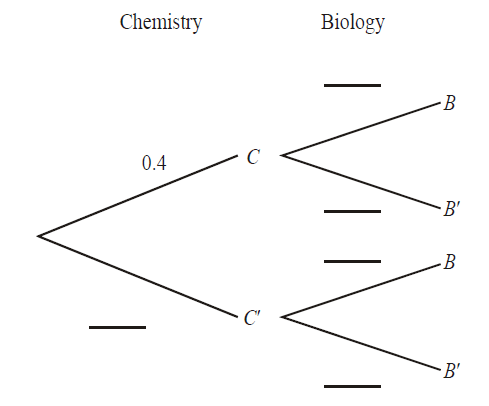
(b) Calculate the probability that a student takes Biology.
(c) Given that a student takes Biology, what is the probability that the student takes Chemistry? [Maximum mark: 5] [with GDC]
Answer/Explanation
Ans.
(a)
(b) P(B) = 0.4(0.6) + 0.6 (0.5) = 0.24 + 0.30= 0.54
(c) P(C | B) = \(\frac{P(B\cap C)}{P(B)}=\frac{0.24}{0.54}=\frac{4}{9}(=0.444,3\;sf)\)
Question
A packet of seeds contains 40% red seeds and 60% yellow seeds. The probability that a red seed grows is 0.9, and that a yellow seed grows is 0.8. A seed is chosen at random from the packet.
(a) Complete the probability tree diagram below.
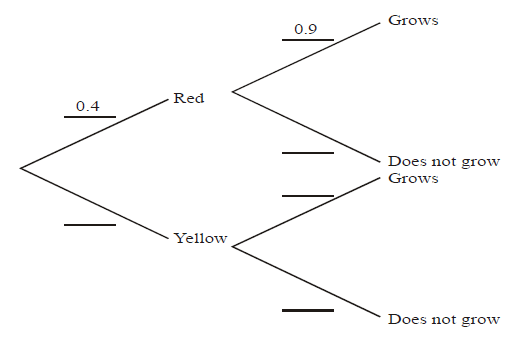
(b) (i) Calculate the probability that the chosen seed is red and grows.
(ii) Calculate the probability that the chosen seed grows.
(iii) Given that the seed grows, calculate the probability that it is red [Maximum mark: 9] [with GDC]
Answer/Explanation
Ans.
(a)
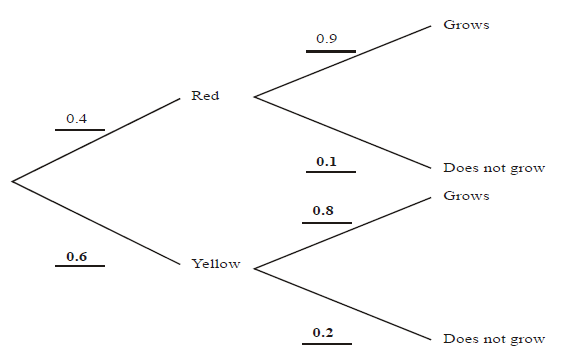
(b) (i) 0.4 x 0.9 = 0.36
(ii) 0.36 + 0.6 x 0.8 (= 0.36 + 0.48) = 0.84
(iii) \(\frac{P(red\cap grows)}{P(grows)}(may\;be\;implied)=\frac{0.36}{0.84}=0.429\left ( \frac{3}{7} \right )\)
Question
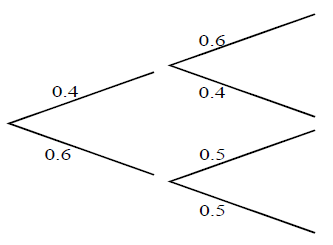
The following probabilities were found for two events R and S .
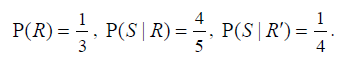
(a) Complete the tree diagram.
(b) Find the following probabilities.
(i) P(R ∩ S) . (ii) P(S) (iii) P(R | S) . [Maximum mark: 10] [without GDC]
Answer/Explanation
Ans.
(a)
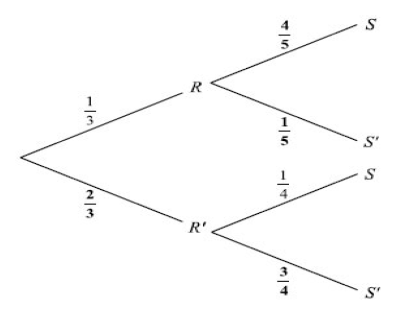
(b) (i) P(R ∩ S) = \(\frac{1}{3}x\frac{4}{5}\left ( =\frac{4}{15}=0.267\right )\)
(ii) P(S) = \(\frac{1}{3}x\frac{4}{5}+\frac{2}{3}x\frac{1}{4}=\frac{13}{30}(=0.433)\)
(iii) P(R | S) = (4/15) / (13/30) =\(\frac{8}{13}(=0.615)\)
Question
The diagram below shows the probabilities for events A and B , with P(A′) = p .
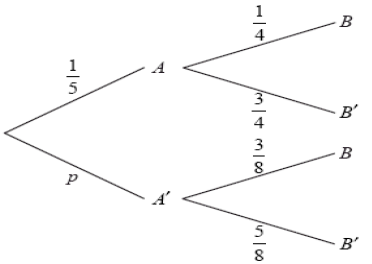
(a) Write down the value of p .
(b) Find P(B) .
(c) Find P(A′ | B) [Maximum mark: 7] [without GDC]
Answer/Explanation
Ans.
(a) p = \(\frac{4}{5}\)
(b) \(\frac{1}{5}x\frac{1}{4}+\frac{4}{5}x\frac{3}{8},\frac{1}{20}+\frac{12}{40}\)
P(B) = \(\frac{1}{5}x\frac{1}{4}+\frac{4}{5}x\frac{3}{8}=\frac{1}{20}+\frac{12}{40}=\frac{14}{40}\left ( =\frac{7}{20} \right )\)
(c) P(A′│B) = \(\frac{\frac{4}{5}x\frac{3}{8}}{\frac{7}{20}}=\frac{12}{14}\left ( =\frac{6}{7} \right )\)
Question
A company uses two machines, A and B, to make boxes. Machine A makes 60 % of the boxes.
80 % of the boxes made by machine A pass inspection.
90 % of the boxes made by machine B pass inspection.
A box is selected at random.
(a) Find the probability that it passes inspection.
(b) The company would like the probability that a box passes inspection to be 0.87.
Find the percentage of boxes that should be made by machine B to achieve this. [Maximum mark: 7] [with GDC]
Answer/Explanation
Ans.
(a) P(pass) = 0.6 × 0.8 + 0.4 × 0.9 = 0.84
(b) P(B) = x, P(A) = 1 – x
0.8(1 – x) + 0.9x = 0.87 ⇔ x = 0.7 70 % from B
Question
In any given season, a soccer team plays 65 % of their games at home.
When the team plays at home, they win 83 % of their games.
When they play away from home, they win 26 % of their games.
The team plays one game.
(a) Find the probability that the team wins the game.
(b) If the team does not win the game, find the probability that the game was played at home. [Maximum mark: 8] [with GDC]
Answer/Explanation
Ans.
(a) P(win) = (0.65)(0.83) + (0.35)(0.26) = 0.6305 (or 0.631)
(b) P(H│W′) = \(\frac{(0.65)(0.17)}{0.3695}\left ( =\frac{0.1105}{0.3695} \right )=0.299\)
Question
A class contains 13 girls and 11 boys. The teacher randomly selects four students.
Determine the probability that all four students selected are girls. [Maximum mark: 6] [with GDC]
Answer/Explanation
Ans.
P(4 girls) = \(\left ( \frac{13}{24}x\frac{12}{23}x\frac{11}{22}x\frac{10}{21} \right )=\frac{17160}{255024}\left ( =\frac{65}{966}=0.0673 \right )\)
Question
A painter has 12 tins of paint. Seven tins are red and five tins are yellow. Two tins are chosen at random. Calculate the probability that both tins are the same colour. [Maximum mark: 6] [with GDC]
Answer/Explanation
Ans.
P(RR) = \(\frac{7}{12}x\frac{6}{11}\left ( =\frac{7}{22} \right )\)
P(YY) = \(\frac{5}{12}x\frac{4}{11}\left ( =\frac{5}{33} \right )\)
P (same colour) = P(RR) + P(YY) = \(\frac{31}{66}\)(= 0.470, 3 sf)