Question: [Maximum mark: 6]
A random sample of nine adults were selected to see whether sleeping well affected their reaction times to a visual stimulus. Each adult’s reaction time was measured twice. The first measurement for reaction time was taken on a morning after the adult had slept well. The second measurement was taken on a morning after the same adult had not slept well. The box and whisker diagrams for the reaction times, measured in seconds, are shown below.
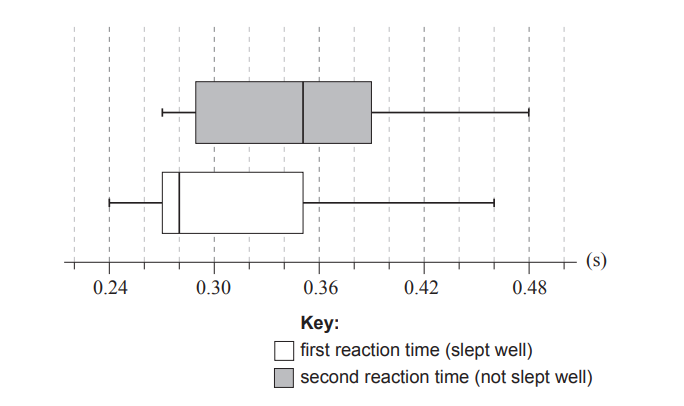
Consider the box and whisker diagram representing the reaction times after sleeping well.
(a) State the median reaction time after sleeping well.
(b) Verify that the measurement of 0.46 seconds is not an outlier.
(c) State why it appears that the mean reaction time is greater than the median reaction time.
Now consider the two box and whisker diagrams.
(d) Comment on whether these box and whisker diagrams provide any evidence that might suggest that not sleeping well causes an increase in reaction time.
▶️Answer/Explanation
Ans:
(a) 0.28(s)
(b) IQR = 0.35 – 0.27 (=0.08) (s)
substituting their IQR into correct expression for upper fence
0.35+1.5×0.08(=0.47)(s)
0.46<0.47
so 0.46 (s) is not an outlier
(c) EITHER
the median is closer to the lower quartile (positively skewed)
OR
the distribution is positively skewed
OR
the range of reaction times below the median is smaller than the range of reaction times above the median
Note: These are sample answers from a range of acceptable correct answers. Award R1 for any correct statement that explains this. Do not award R1 if there is also an incorrect statement, even if another statement in the answer is correct. Accept a correctly and clearly labelled diagram.
(d) EITHER
the distribution for ‘not sleeping well’ is centred at a higher reaction time
OR
the median reaction time after not sleeping well is equal to the upper quartile reaction time after sleeping well
OR
75% of reaction times are <0.35 seconds after sleeping well, compared with 50% after not sleeping well
OR
the sample size of 9 is too small to draw any conclusions
Note: These are sample answers from a range of acceptable correct answers. Accept any relevant correct statement that relates to the median and/or quartiles shown in the box plots. Do not accept a comparison of means. Do not award R1 if there is also an incorrect statement, even if another statement in the answer is correct Award R0 to “correlation does not imply causation”.
Question
A research student weighed lizard eggs in grams and recorded the results. The following box and whisker diagram shows a summary of the results where L and U are the lower and upper quartiles respectively.
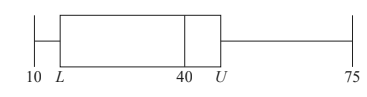
diagram not to scale
The interquartile range is 20 grams and there are no outliers in the results.
(a) Find the minimum possible value of U . [3]
(b) Hence, find the minimum possible value of L . [2]
▶️Answer/Explanation
Ans:

Question
A scientist has 100 female fish and 100 male fish. She measures their lengths to the nearest cm. These are shown in the following box and whisker diagrams.
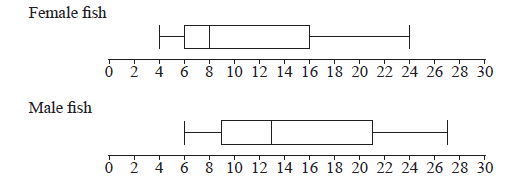
Find the range of the lengths of all 200 fish.[3]
Four cumulative frequency graphs are shown below.
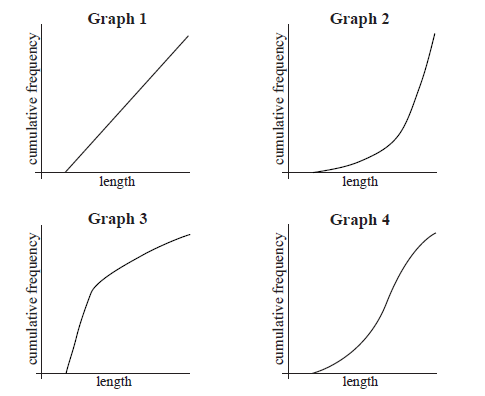
Which graph is the best representation of the lengths of the female fish?[2]
▶️Answer/Explanation
Markscheme
correct end points (A1)(A1)
max = 27 , min = 4
range = 23 A1 N3
[3 marks]
Graph 3 A2 N2
[2 marks]
Question
The weekly wages (in dollars) of 80 employees are displayed in the cumulative frequency curve below.
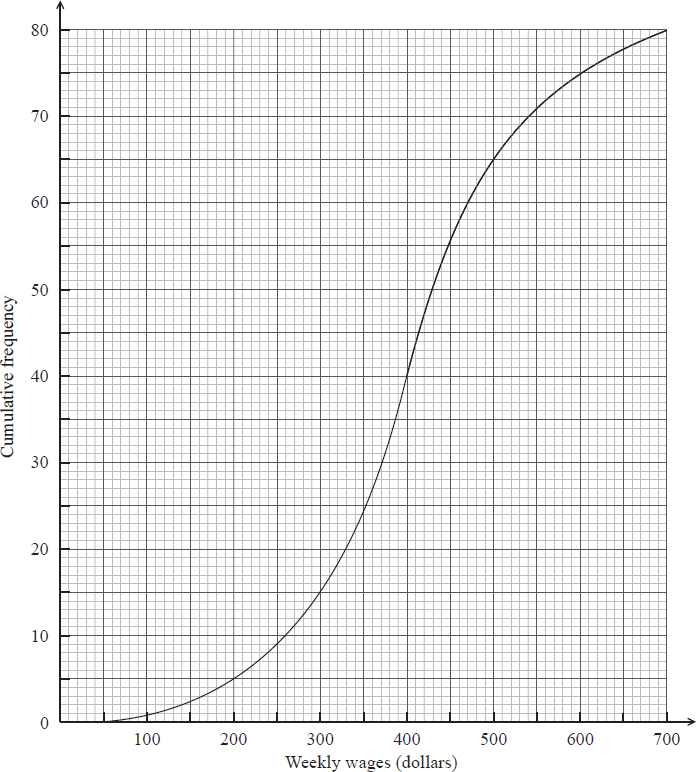
a(i) and (ii).(i) Write down the median weekly wage.
(ii) Find the interquartile range of the weekly wages.[4]
The box-and-whisker plot below displays the weekly wages of the employees.
Write down the value of
(i) \(a\) ;
(ii) \(b\) ;
(iii) \(c\) .[3]
Find the median number of hours worked per week.[3]
Find the number of employees who work more than \(25\) hours per week.[5]
▶️Answer/Explanation
Markscheme
(i) median weekly wage \(= 400\) (dollars) A1 N1
(ii) lower quartile \(= 330\), upper quartile \(= 470\) (A1)(A1)
\({\text{IQR}} = 140\) (dollars) (accept any notation suggesting interval \(330\) to \(470\)) A1 N3
Note: Exception to the FT rule. Award A1(FT) for an incorrect IQR only if both quartiles are explicitly noted.
[4 marks]
(i) \(330\) (dollars) A1 N1
(ii) \(400\) (dollars) A1 N1
(iii) \(700\) (dollars) A1 N1
[3 marks]
valid approach (M1)
e.g. \({\rm{hours = }}\frac{{{\rm{wages}}}}{{{\rm{rate}}}}\)
correct substitution (A1)
e.g. \(\frac{{400}}{{20}}\)
median hours per week \(= 20\) A1 N2
[3 marks]
attempt to find wages for 25 hours per week (M1)
e.g. \({\text{wages}} = {\text{hours}} \times {\text{rate}}\)
correct substitution (A1)
e.g. \(25 \times 20\)
finding wages \(= 500\) (A1)
65 people (earn 500\( \leqslant \)) (A1)
15 people (work more than 25 hours) A1 N3
[5 marks]
Question
The following box-and-whisker plot shows the number of text messages sent by students in a school on a particular day.
a.Find the value of the interquartile range.[2]
b.One student sent k text messages, where k > 11 . Given that k is an outlier, find the least value of k.[4]
▶️Answer/Explanation
Markscheme
a.recognizing Q1 or Q3 (seen anywhere) (M1)
eg 4,11 , indicated on diagram
IQR = 7 A1 N2
[2 marks]
recognizing the need to find 1.5 IQR (M1)
eg 1.5 × IQR, 1.5 × 7
valid approach to find k (M1)
eg 10.5 + 11, 1.5 × IQR + Q3
21.5 (A1)
k = 22 A1 N3
Note: If no working shown, award N2 for an answer of 21.5.
[4 marks]
