IB Mathematics AHL 1.13 Modulus–argument (polar) form AI HL Paper 2- Exam Style Questions- New Syllabus
Question
(ii) Calculate the total length of the fractal structure after 10 full stages of growth.
(iii) Determine whether the total length of the branches approaches a finite limit if the process continues indefinitely. Justify your conclusion.
(ii) Hence, find the coordinates of \(b\) in Cartesian form, \(a + bi\), where \(a, b \in \mathbb{R}\).
Most-appropriate topic codes:
• TOPIC SL 1.3: Geometric sequences and series — part (b)
• TOPIC AHL 1.13: Geometric interpretation of complex numbers — part (c)
▶️ Answer/Explanation
(a)
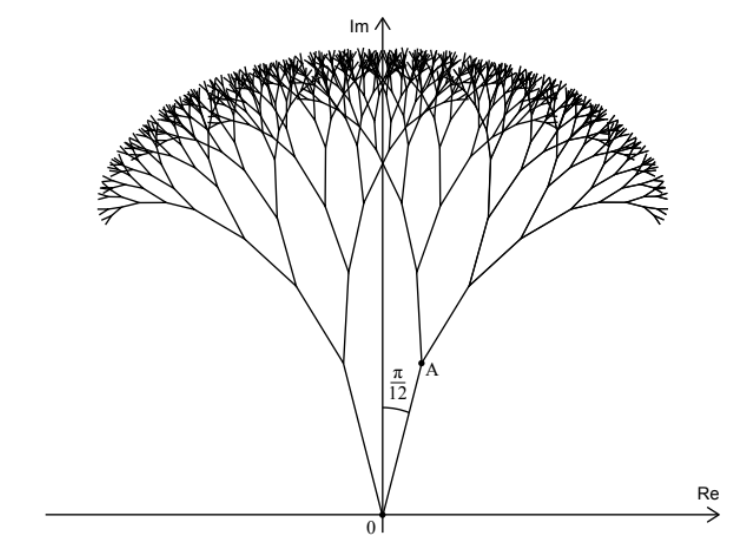
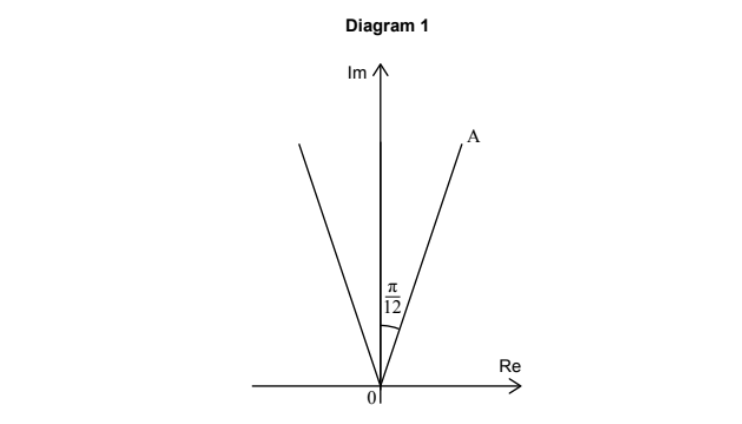
The initial segment on the imaginary axis has an argument of \(\frac{\pi}{2}\).
Point A is formed by a clockwise rotation of \(\frac{\pi}{12}\).
Argument \(= \frac{\pi}{2} – \frac{\pi}{12} = \frac{5\pi}{12}\).
Modulus is 5.
\(A = \mathbf{5e^{\frac{5\pi}{12}i}}\).
(b)
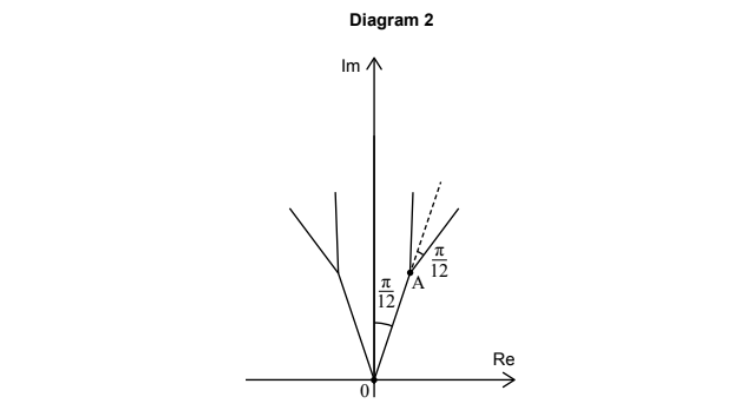
(i) Stage 1: 2 branches of length 5. Total = \(10\).
Stage 2: 4 branches of length \(5 \times 0.7 = 3.5\). Total = \(14\).
Total Length \(= 10 + 14 = \mathbf{24}\) (AG).
(ii) This is a geometric series where \(u_1 = 10\) and the common ratio \(r = 2 \times 0.7 = 1.4\).
\(S_{10} = \frac{10(1.4^{10} – 1)}{1.4 – 1} \approx \mathbf{698}\).
(iii) Since \(|r| = 1.4 > 1\), the geometric series diverges. There is no finite limit.
(c)
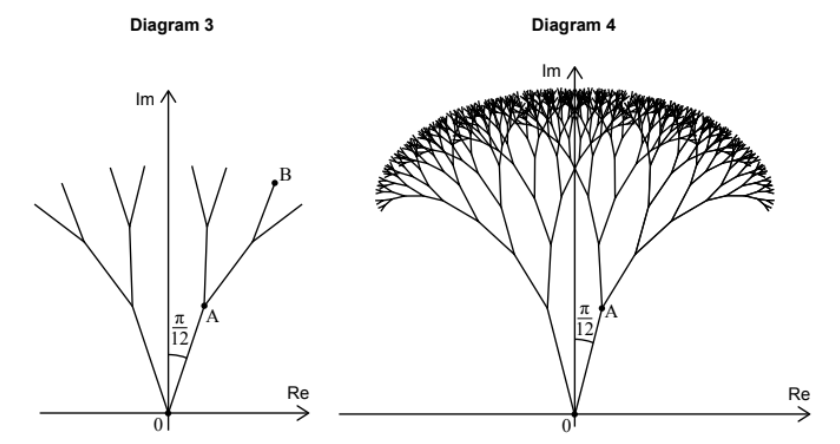
(i) To find \(b\), we sum the vectors for each stage of the branch leading to \(B\):
Correct moduli: \(5\), \(5 \times 0.7 = 3.5\), \(5 \times 0.7^2 = 2.45\).
Arguments are calculated by adding/subtracting \(\frac{\pi}{12}\) at each junction: \(\frac{5\pi}{12}\), \(\frac{4\pi}{12}\) (or \(\frac{\pi}{3}\)), and \(\frac{5\pi}{12}\).
\(b = 5e^{\frac{5\pi}{12}i} + 3.5e^{\frac{\pi}{3}i} + 2.45e^{\frac{5\pi}{12}i}\).
(Using 3 s.f. decimals: \(b = 5e^{1.31i} + 3.5e^{1.05i} + 2.45e^{1.31i}\)).
(ii) Converting to Cartesian form:
\(b = (3.67820… + 10.2272…i)\).
\(b = \mathbf{3.68 + 10.2i}\).
Note: \(3.66 + 10.2i\) is also acceptable if 3 s.f. values were used during calculation.
