Question
The graph of \(y = \ln (x)\) is transformed into the graph of \(y = \ln \left( {2x + 1} \right)\) .
a.Describe two transformations that are required to do this.[2]
b.Solve \(\ln \left( {2x + 1} \right) > 3\cos (x)\), \(x \in [0,10]\).[4]
▶️Answer/Explanation
Markscheme
EITHER
translation of \( – \frac{1}{2}\) parallel to the \(x\)-axis
stretch of a scale factor of \(\frac{1}{2}\) parallel to the \(x\)-axis A1A1
OR
stretch of a scale factor of \(\frac{1}{2}\) parallel to the \(x\)-axis
translation of \( – 1\) parallel to the \(x\)-axis A1A1
Note: Accept clear alternative terminologies for either transformation.
[2 marks]
EITHER
\(1.16 < x < 5.71 \cup 6.75 < x \leqslant 10\) A1A1A1A1
OR
]\(1.16\), \(5.71\)[ \(\cup\) ]\(6.75\), \(10\)] A1A1A1A1
Note: Award A1 for 1 intersection value, A1 for the other 2, A1A1 for the intervals.
[6 marks]
Examiners report
This question was well done by many candidates. It would appear, however, that few candidates were aware of the standard terminology – Stretch and Translation – used to describe the relevant graph transformations. Most made good use of a GDC to find the critical points and to help in deciding on the correct intervals. A significant minority failed to note \(x = 10\) as an endpoint.
This question was well done by many candidates. It would appear, however, that few candidates were aware of the standard terminology – Stretch and Translation – used to describe the relevant graph transformations. Most made good use of a GDC to find the critical points and to help in deciding on the correct intervals. A significant minority failed to note \(x = 10\) as an endpoint.
Question
Let \(f(x) = \ln x\) . The graph of f is transformed into the graph of the function g by a translation of \(\left( {\begin{array}{*{20}{c}}
3 \\
{ – 2}
\end{array}} \right)\), followed by a reflection in the x-axis. Find an expression for \(g(x)\), giving your answer as a single logarithm.
▶️Answer/Explanation
Markscheme
\(h(x) = f(x – 3) – 2 = \ln (x – 3) – 2\) (M1)(A1)
\(g(x) = -h(x) = 2 – \ln (x – 3)\) M1
Note: Award M1 only if it is clear the effect of the reflection in the x-axis:
the expression is correct OR
there is a change of signs of the previous expression OR
there’s a graph or an explanation making it explicit
\( = \ln {{\text{e}}^2} – \ln (x – 3)\) M1
\( = \ln \left( {\frac{{{{\text{e}}^2}}}{{x – 3}}} \right)\) A1
[5 marks]
Question
The graph of \(y = \ln (5x + 10)\) is obtained from the graph of \(y = \ln x\) by a translation of \(a\) units in the direction of the \(x\)-axis followed by a translation of \(b\) units in the direction of the \(y\)-axis.
a.Find the value of \(a\) and the value of \(b\).[4]
b.The region bounded by the graph of \(y = \ln (5x + 10)\), the \(x\)-axis and the lines \(x = {\text{e}}\) and \(x = 2{\text{e}}\), is rotated through \(2\pi \) radians about the \(x\)-axis. Find the volume generated.[2]
▶️Answer/Explanation
Markscheme
EITHER
\(y = \ln (x – a) + b = \ln (5x + 10)\) (M1)
\(y = \ln (x – a) + \ln c = \ln (5x + 10)\)
\(y = \ln \left( {c(x – a)} \right) = \ln (5x + 10)\) (M1)
OR
\(y = \ln (5x + 10) = \ln \left( {5(x + 2)} \right)\) (M1)
\(y = \ln (5) + \ln (x + 2)\) (M1)
THEN
\(a = – 2,{\text{ }}b = \ln 5\) A1A1
Note: Accept graphical approaches.
Note: Accept \(a = 2,{\text{ }}b = 1.61\)
[4 marks]
\(V = \pi {\int_e^{2e} {\left[ {\ln (5x + 10)} \right]} ^2}{\text{d}}x\) (M1)
\( = 99.2\) A1
[2 marks]
Total [6 marks]
Examiners report
[N/A]
[N/A]
Question
When carpet is manufactured, small faults occur at random. The number of faults in Premium carpets can be modelled by a Poisson distribution with mean 0.5 faults per 20\(\,\)m2. Mr Jones chooses Premium carpets to replace the carpets in his office building. The office building has 10 rooms, each with the area of 80\(\,\)m2.
a.Find the probability that the carpet laid in the first room has fewer than three faults.[3]
b.Find the probability that exactly seven rooms will have fewer than three faults in the carpet.[3]
▶️Answer/Explanation
Markscheme
\(\lambda = 4 \times 0.5\) (M1)
\(\lambda = 2\) (A1)
\({\text{P}}(X \leqslant 2) = 0.677\) A1
[3 marks]
\(Y \sim B(10,{\text{ }}0,677)\) (M1)(A1)
\({\text{P}}(Y = 7) = 0.263\) A1
Note: Award M1 for clear recognition of binomial distribution.
[3 marks]
Examiners report
[N/A]
[N/A]
Question
Consider the following graph of a function y = f(x)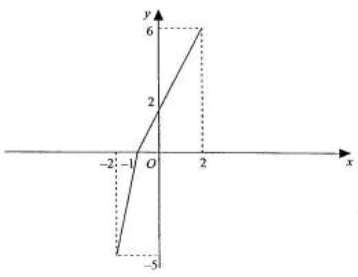
Sketch the graphs of the following functions (a) y = f(x) – 1 (b) \(y = \frac{f(x)}{x}\) (c) y = -f(x) (d) y = f(x-1) (e) \(y = f(\frac{x}{2})\) (f) y = f(-x) (g) \(y=\begin{vmatrix}f(x)\end{vmatrix}\) (h) \(y=f(\begin{vmatrix} x \end{vmatrix})\) (g)\(=2f(\frac{1}{2}(x-1))\)
▶️Answer/Explanation
Ans
Solutions are not provided
