Question 1 [Maximum mark: 15]
A farmer owns a field in the shape of a triangle ABC such that AB = 650 m, AC = 1005 m
and BC = 1225 m
diagram not to scale
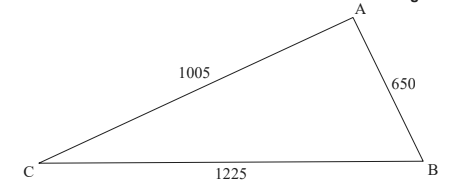
a. Find the size of AĈB. [3]
The local town is planning to build a highway that will intersect the borders of the field at points D and E, where DC = 210 m and CÊD = 100° , as shown in the diagram below.
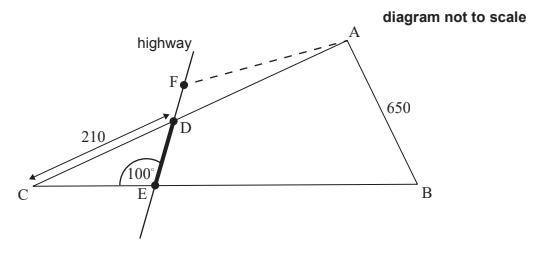
b. Find DE. [3]
The town wishes to build a carpark here. They ask the farmer to exchange the part of the field represented by triangle DCE. In return the farmer will get a triangle of equal area ADF, where F lies on the same line as D and E, as shown in the diagram above.
c. Find the area of triangle DCE. [5]
d. Estimate DF. You may assume the highway has a width of zero. [4]
▶️Answer/Explanation
(a) cosine rule ACB = \(cos^{-1}(\frac{1005^{2}+1225^{2}-650^{2}}{2\times 1005\times 1225})\)
\(= 32.0 ((31.9980…)\) OR \(0.558 (0.558471…)\)
(b) sine rule \(\frac{DE}{sin31.9980..}= \frac{210}{sin100}\)
\(DE = 113 m (112.9937…)\)
(c) \(180-(100 +their part (a))=48.0019\) OR
\(0.837791…\(\frac{1}{2}\times 112.9937…\times 210\times sin48.002\)
\(8820m^{2}\rightarrow (8817.18 )\)
(d) \(1005 − 210 \) OR \(795\)
equating answer to part (c) to area of a triangle formula
\(8817.18..=\frac{1}{2}\times DF\times (1005-210)\times sin48.002..\)
\((DF=)29.8m(29.8473….)\)
Question
A sector of a circle, centre O and radius 4.5m, is shown in the following diagram.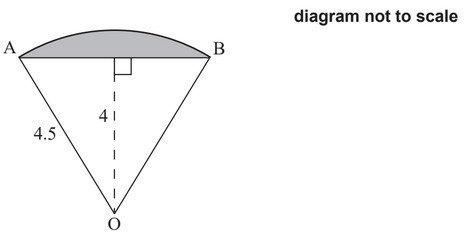
(a) (i) Find the angle AÔB.
(ii) Find the area of the shaded segment.
A square field with side 8m has a goat tied to a post in the centre by a rope such that the
goat can reach all parts of the field up to 4.5m from the post.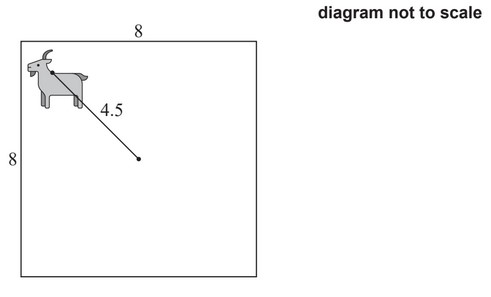
(b) Find the area of the field that can be reached by the goat.
Let V be the volume of grass eaten by the goat, in cubic metres, and t be the length of time,
in hours, that the goat has been in the field.
The goat eats grass at the rate of \(\frac{dV}{dt}=0.3te^{-t}\).
(c) Find the value of t at which the goat is eating grass at the greatest rate.
The goat is tied in the field for 8 hours.
(d) Find the total volume of grass eaten by the goat during this time.
▶️Answer/Explanation
Ans:


Question
Hyungmin designs a concrete bird bath. The bird bath is supported by a pedestal. This is shown in the diagram.
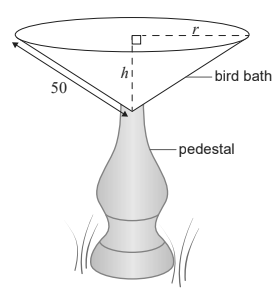
The interior of the bird bath is in the shape of a cone with radius r , height h and a constant slant height of 50 cm.
Write down an equation in r and h that shows this information. [1] Let V be the volume of the bird bath.
Show that V = \(\frac{2500\pi h}{3}-\frac{\pi h^3}{3}\) . [1]
Find \(\frac{dV}{dh}\) . [2]
Hyungmin wants the bird bath to have maximum volume.
Using your answer to part (c), find the value of h for which V is a maximum. [2]
Find the maximum volume of the bird bath. [2] To prevent leaks, a sealant is applied to the interior surface of the bird bath.
Find the surface area to be covered by the sealant, given that the bird bath has
▶️Answer/Explanation
Ans:
(a) \(h^{2}+r^{2}= 50^{2}\) (or equivalent)
(b)
\(\frac{1}{3}\times \pi \times (2500-h^{2})\times h \)
\( V= \frac{2500\pi h}{3}- \frac{\pi h^{3}}{3}\)
(c) \(\frac{dv}{dh}=\frac{2500\pi }{3}-\pi h^{2}\)
(d)
o= \(\frac{25000\pi }{3}-\pi h^{2}\)OR sketch of \(\frac{dv}{dh}\)
\((h= )28.9(cm)\sqrt{\frac{2500}{3}},\frac{50}{\sqrt{3}}\) \(\frac{50\sqrt{3}}{3}\), 28.8675..
(e) (V=)\(\frac{2500\times \pi 28.8675…}{3}-\frac{\pi (28.8675..)^{3}}{3}\)OR \(\frac{1}{3}\pi (40.828…)^{2}\times 28.8675\)…(v=)50400\((cm^{3})(50383.3…)\)
(f)(S=)\(\pi \times \sqrt{2500-(28.86675…)^{2}}\times 50\) (S=) \(6410(cm^{2})(6412.74….)\)
Question
Daniel wants to invest \(\$ 25\,000\) for a total of three years. There are two investment options.
Option One pays compound interest at a nominal annual rate of interest of 5 %, compounded annually.
Option Two pays compound interest at a nominal annual rate of interest of 4.8 %, compounded monthly.
An arithmetic sequence is defined as
un = 135 + 7n, n = 1, 2, 3, …
A.a.Calculate the value of his investment at the end of the third year for each investment option, correct to two decimal places.[8]
A.b.Determine Daniel’s best investment option.[1]
B.a.Calculate u1, the first term in the sequence.[2]
B.b.Show that the common difference is 7.[2]
B.c.Sn is the sum of the first n terms of the sequence.
Find an expression for Sn. Give your answer in the form Sn = An2 + Bn, where A and B are constants.[3]
B.d.The first term, v1, of a geometric sequence is 20 and its fourth term v4 is 67.5.
Show that the common ratio, r, of the geometric sequence is 1.5.[2]
B.e.Tn is the sum of the first n terms of the geometric sequence.
Calculate T7, the sum of the first seven terms of the geometric sequence.[2]
B.f.Tn is the sum of the first n terms of the geometric sequence.
Use your graphic display calculator to find the smallest value of n for which Tn > Sn.[2]
▶️Answer/Explanation
Markscheme
Option 1: Amount \( = 25\,000{\left( {1 + \frac{5}{{100}}} \right)^3}\) (M1)(A1)
= \(28\,940.63\) (A1)(G2)
Note: Award (M1) for substitution in compound interest formula, (A1) for correct substitution. Give full credit for use of lists.
Option 2: Amount \( = 25\,000{\left( {1 + \frac{{4.8}}{{12(100)}}} \right)^{3 \times 12}}\) (M1)
= \(28\,863.81\) (A1)(G2)
Note: Award (M1) for correct substitution in the compound interest formula. Give full credit for use of lists.[8 marks]
Option 1 is the best investment option. (A1)(ft)[1 mark]
u1 = 135 + 7(1) (M1)
= 142 (A1)(G2)[2 marks]
u2 = 135 + 7(2) = 149 (M1)
d = 149 – 142 OR alternatives (M1)(ft)
d = 7 (AG)[2 marks]
\({S_n} = \frac{{n[2(142) + 7(n – 1)]}}{2}\) (M1)(ft)
Note: Award (M1) for correct substitution in correct formula.
\( = \frac{{n[277 + 7n]}}{2}\) OR equivalent (A1)
\( = \frac{{7{n^2}}}{2} + \frac{{277n}}{2}\) (= 3.5n2 + 138.5n) (A1)(G3)[3 marks]
20r3 = 67.5 (M1)
r3 = 3.375 OR \(r = \sqrt[3]{{3.375}}\) (A1)
r = 1.5 (AG)[2 marks]
\({T_7} = \frac{{20({{1.5}^7} – 1)}}{{(1.5 – 1)}}\) (M1)
Note: Award (M1) for correct substitution in correct formula.
= 643 (accept 643.4375) (A1)(G2)[2 marks]
\(\frac{{20({{1.5}^n} – 1)}}{{(1.5 – 1)}} > \frac{{7{n^2}}}{2} + \frac{{277n}}{2}\) (M1)
Note: Award (M1) for an attempt using lists or for relevant graph.
n = 10 (A1)(ft)(G2)
Note: Follow through from their (c).[2 marks]
