Question
Using geometry software, Pedro draws a quadrilateral ABCD. AB = 8 cm and CD = 9 cm .
Angle BAD = 51.5° and angle ADB = 52.5° . This information is shown in the diagram.
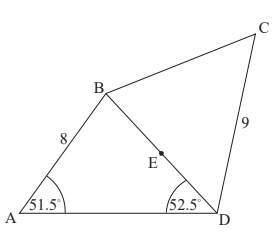
Calculate the length of BD. [3]
CE = 7 cm , where point E is the midpoint of BD.
- Show that angle EDC = 48.0° , correct to three significant figures. [4]
- Calculate the area of triangle BDC. [3]
Pedro draws a circle, with centre at point E, passing through point C. Part of the circle is shown in the diagram.
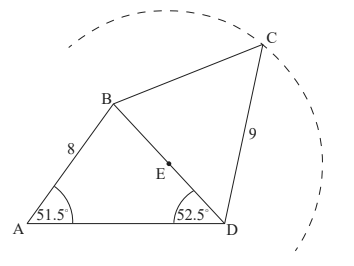
Show that point A lies outside this circle. Justify your reasoning. [5]
▶️Answer/Explanation
Ans:
(a) \(\frac{BD}{sin51.5}\)= \(\frac{8}{sin52.5}(BD=)7.89(cm)(7.89164…)\)
(b)cosEDC= \(\frac{9^{2}+3.94582…^{2}-7^{2}}{2\times 9\times 3.94582…}\)(EDC=)47.9515…48.0(3 sig figures)
(c) (area =) \(\frac{1}{2}\times 7.89164…\times 9\times sin48.0 (area =)\)26.4 \(cm^{2}\)(26.3908…)
(d)
\(AE^{2}= 8^{2}+ (3.94582…)^{2}-2\times 8\times 3.94582…cos(76)\) (AE=)8.02 (cm)(8.01849…) OR \(AE^{2}= 9.78424…^{2}+ (3.94582….)^{2}-2\times 9.78424…\times 3.94582…cos(52.5)(AE=)8.02(cm)\)(8.01849…)8.02>7
Question
Jenny has a circular cylinder with a lid. The cylinder has height 39 cm and diameter 65 mm.
An old tower (BT) leans at 10° away from the vertical (represented by line TG).
The base of the tower is at B so that \({\text{M}}\hat {\rm B}{\text{T}} = 100^\circ \).
Leonardo stands at L on flat ground 120 m away from B in the direction of the lean.
He measures the angle between the ground and the top of the tower T to be \({\text{B}}\hat {\rm L}{\text{T}} = 26.5^\circ \).
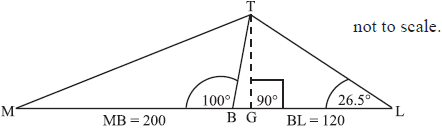
i.a.Calculate the volume of the cylinder in cm3. Give your answer correct to two decimal places.[3]
i.b.The cylinder is used for storing tennis balls. Each ball has a radius of 3.25 cm.
Calculate how many balls Jenny can fit in the cylinder if it is filled to the top.[1]
i.c.(i) Jenny fills the cylinder with the number of balls found in part (b) and puts the lid on. Calculate the volume of air inside the cylinder in the spaces between the tennis balls.
(ii) Convert your answer to (c) (i) into cubic metres.[4]
ii.a.(i) Find the value of angle \({\text{B}}\hat {\rm T}{\text{L}}\).
(ii) Use triangle BTL to calculate the sloping distance BT from the base, B to the top, T of the tower.[5]
ii.b.Calculate the vertical height TG of the top of the tower.[2]
ii.c.Leonardo now walks to point M, a distance 200 m from B on the opposite side of the tower. Calculate the distance from M to the top of the tower at T.[3]
▶️Answer/Explanation
Markscheme
\(\pi \times 3.25^2 \times 39\) (M1)(A1)
(= 1294.1398)
Answer 1294.14 (cm3)(2dp) (A1)(ft)(G2)
(UP) not applicable in this part due to wording of question. (M1) is for substituting appropriate numbers from the problem into the correct formula, even if the units are mixed up. (A1) is for correct substitutions or correct answer with more than 2dp in cubic centimetres seen. Award (G1) for answer to > 2dp with no working and no attempt to correct to 2dp. Award (M1)(A0)(A1)(ft) for \(\pi \times {32.5^2} \times 39{\text{ c}}{{\text{m}}^3}\) (= 129413.9824) = 129413.98
Use of \(\pi = \frac{22}{7}\) or 3.142 etc is premature rounding and is awarded at most (M1)(A1)(A0) or (M1)(A0)(A1)(ft) depending on whether the intermediate value is seen or not. For all other incorrect substitutions, award (M1)(A0) and only follow through the 2 dp correction if the intermediate answer to more decimal places is seen. Answer given as a multiple of \(\pi\) is awarded at most (M1)(A1)(A0). As usual, an unsubstituted formula followed by correct answer only receives the G marks.[3 marks]
39/6.5 = 6 (A1)[1 mark]
Unit penalty (UP) is applicable where indicated in the left hand column.
(UP) (i) Volume of one ball is \(\frac{4}{3} \pi \times 3.25^3 {\text{ cm}}^3\) (M1)
\({\text{Volume of air}} = \pi \times {3.25^2} \times 39 – 6 \times \frac{4}{3}\pi \times {3.25^3} = 431{\text{ c}}{{\text{m}}^3}\) (M1)(A1)(ft)(G2)
Award first (M1) for substituted volume of sphere formula or for numerical value of sphere volume seen (143.79… or 45.77… \( \times \pi\)). Award second (M1) for subtracting candidate’s sphere volume multiplied by their answer to (b). Follow through from parts (a) and (b) only, but negative or zero answer is always awarded (A0)(ft)
(UP) (ii) 0.000431m3 or 4.31×10−4 m3 (A1)(ft) [4 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
(i) \({\text{Angle B}}\widehat {\text{T}}{\text{L}} = 180 – 80 – 26.5\) or \(180 – 90 – 26.5 – 10\) (M1)
\(= 73.5^\circ\) (A1)(G2)
(ii) \(\frac{{BT}}{{\sin (26.5^\circ )}} = \frac{{120}}{{\sin (73.5^\circ )}}\) (M1)(A1)(ft)
(UP) BT = 55.8 m (3sf) (A1)(ft)[5 marks]
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but
negative lengths are always awarded (A0)(ft).
The answers are (all 3sf)
(ii)(a) – 124 m (A0)(ft)
(ii)(b) 123 m (A0)
(ii)(c) 313 m (A0)
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but negative lengths are always awarded (A0)(ft)
Unit penalty (UP) is applicable where indicated in the left hand column.
TG = 55.8sin(80°) or 55.8cos(10°) (M1)
(UP) = 55.0 m (3sf) (A1)(ft)(G2)
Apply (AP) if 0 missing[2 marks]
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but
negative lengths are always awarded (A0)(ft).
The answers are (all 3sf)
(ii)(a) – 124 m (A0)(ft)
(ii)(b) 123 m (A0)
(ii)(c) 313 m (A0)
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but negative lengths are always awarded (A0)(ft)
Unit penalty (UP) is applicable where indicated in the left hand column.
\({\text{MT}}^2 = 200^2 + 55.8^2 – 2 \times 200 \times 55.8 \times \cos(100^\circ)\) (M1)(A1)(ft)
(UP) MT = 217 m (3sf) (A1)(ft)
Follow through only from part (ii)(a)(ii). Award marks at discretion for any valid alternative method.[3 marks]
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but
negative lengths are always awarded (A0)(ft).
The answers are (all 3sf)
(ii)(a) – 124 m (A0)(ft)
(ii)(b) 123 m (A0)
(ii)(c) 313 m (A0)
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but negative lengths are always awarded (A0)(ft)
Question
Mal is shopping for a school trip. He buys \(50\) tins of beans and \(20\) packets of cereal. The total cost is \(260\) Australian dollars (\({\text{AUD}}\)).
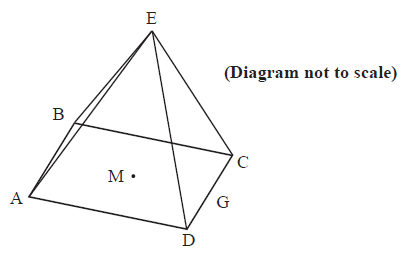
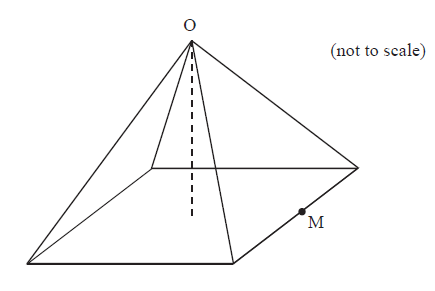
The triangular faces of a square based pyramid, \({\text{ABCDE}}\), are all inclined at \({70^ \circ }\) to the base. The edges of the base \({\text{ABCD}}\) are all \(10{\text{ cm}}\) and \({\text{M}}\) is the centre. \({\text{G}}\) is the mid-point of \({\text{CD}}\).
i.a.Write down an equation showing this information, taking \(b\) to be the cost of one tin of beans and \(c\) to be the cost of one packet of cereal in \({\text{AUD}}\).[1]
i.b.Stephen thinks that Mal has not bought enough so he buys \(12\) more tins of beans and \(6\) more packets of cereal. He pays \(66{\text{ AUD}}\).
Write down another equation to represent this information.[1]
i.c.Stephen thinks that Mal has not bought enough so he buys \(12\) more tins of beans and \(6\) more packets of cereal. He pays \(66{\text{ AUD}}\).
Find the cost of one tin of beans.[2]
i.d.(i) Sketch the graphs of the two equations from parts (a) and (b).
(ii) Write down the coordinates of the point of intersection of the two graphs.[4]
ii.a.Using the letters on the diagram draw a triangle showing the position of a \({70^ \circ }\) angle.[1]
ii.b.Show that the height of the pyramid is \(13.7{\text{ cm}}\), to 3 significant figures.[2]
ii.c.Calculate
(i) the length of \({\text{EG}}\);
(ii) the size of angle \({\text{DEC}}\).[4]
ii.d.Find the total surface area of the pyramid.[2]
▶️Answer/Explanation
Markscheme
\(50b + 20c = 260\) (A1)[1 mark]
\(12b + 6c = 66\) (A1)[1 mark]
Solve to get \(b = 4\) (M1)(A1)(ft)(G2)
Note: (M1) for attempting to solve the equations simultaneously.[2 marks]
(i)
 (A1)(A1)(A1)
(A1)(A1)(A1)
Notes: Award (A1) for labels and some idea of scale, (A1)(ft)(A1)(ft) for each line.
The axis can be reversed.
(ii) \((4,3)\) or \((3,4)\) (A1)(ft)
Note: Accept \(b = 4\), \(c = 3\)[4 marks]
 (A1)
(A1)
[1 mark]
\(\tan 70 = \frac{h}{5}\) (M1)
\(h = 5\tan 70 = 13.74\) (A1)
\(h = 13.7{\text{ cm}}\) (AG)[2 marks]
Unit penalty (UP) is applicable in this part of the question where indicated in the left hand column.
(i) \({\text{E}}{{\text{G}}^2} = {5^2} + {13.7^2}\) OR \({5^2} + {(5\tan 70)^2}\) (M1)
(UP) \({\text{EG}} = 14.6{\text{ cm}}\) (A1)(G2)
(ii) \({\text{DEC}} = 2 \times {\tan ^{ – 1}}\left( {\frac{5}{{14.6}}} \right)\) (M1)
\( = {37.8^ \circ }\) (A1)(ft)(G2)[4 marks]
Unit penalty (UP) is applicable in this part of the question where indicated in the left hand column.
\({\text{Area}} = 10 \times 10 + 4 \times 0.5 \times 10 \times 14.619\) (M1)
(UP) \( = 392{\text{ c}}{{\text{m}}^2}\) (A1)(ft)(G2)[2 marks]
Unit penalty (UP) is applicable in this part of the question where indicated in the left hand column.
\({\text{Volume}} = \frac{1}{3} \times 10 \times 10 \times 13.7\) (M1)
(UP) \( = 457{\text{ c}}{{\text{m}}^3}\) (\(458{\text{ c}}{{\text{m}}^3}\)) (A1)(G2)[2 marks]
Question
Amir needs to construct an isosceles triangle \({\text{ABC}}\) whose area is \(100{\text{ cm}}^2\). The equal sides, \({\text{AB}}\) and \({\text{BC}}\), are \(20{\text{ cm}}\) long.
Sylvia is making a square-based pyramid. Each triangle has a base of length \(12{\text{ cm}}\) and a height of \(10{\text{ cm}}\).
i.a.Angle \({\text{ABC}}\) is acute. Show that the angle \({\text{ABC}}\) is \({30^ \circ }\).[2]
i.b.Find the length of \({\text{AC}}\).[3]
ii.a.Show that the height of the pyramid is \(8{\text{ cm}}\).[2]
ii.b.\({\text{M}}\) is the midpoint of the base of one of the triangles and \({\text{O}}\) is the apex of the pyramid.
Find the angle that the line \({\text{MO}}\) makes with the base of the pyramid.[3]
ii.c.Calculate the volume of the pyramid.[2]
ii.d.Daniel wants to make a rectangular prism with the same volume as that of Sylvia’s pyramid. The base of his prism is to be a square of side \(10{\text{ cm}}\). Calculate the height of the prism.[2]
▶️Answer/Explanation
Markscheme
\(\frac{1}{2}{20^2}\sin B = 100\) (M1)(A1)
\(B = {30^ \circ }\) (AG)
Note: (M1) for correct substituted formula and (A1) for correct substitution. \(B = {30^ \circ }\) must be seen or previous (A1) mark is lost.[2 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
\({\overline {{\text{AC}}} ^2} = 2 \times {20^2} – 2 \times {20^2} \times \cos {30^ \circ }\) (M1)(A1)
(UP) \(\overline {{\text{AC}}} = 10.4{\text{ cm}}\) (A1)(G2)
Note: (M1) for using cosine rule, (A1) for correct substitution. Last (A1) is for the correct answer. Accept use of sine rule or any correct method e.g. \({\text{AC}} = 2 \times 20\sin {15^ \circ }\) .[3 marks]
\({x^2} + {6^2} = {10^2}\) (A1)(M1)
\(x = 8{\text{ cm}}\) (AG)
Note: (A1) for \(6\) (or \(36\)) seen and (M1) for using Pythagoras with correct substitution. \(x = 8\) must be seen or previous (M1) mark is lost.[2 marks]
\(\cos \beta = \frac{6}{{10}}\) (M1)(A1)
\(\beta = {53.1^ \circ }\) (A1)(G2)
OR equivalent
Note: (M1) for use of trigonometric ratio with numbers from question. (A1) for use of correct numbers, and (A1) for correct answer.[3 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
\(vol = \frac{{{{12}^2} \times 8}}{3}\) (M1)
(UP) \( = 384{\text{ c}}{{\text{m}}^3}\) (A1)(G2)
Note: (M1) for correct formula and correct substitution, (A1) for correct answer.[2 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
Let h be the height
\({10^2}h = 384\) (M1)
(UP) \( = 3.84{\text{ cm}}\) (A1)(ft)(G2)
Note: (M1) for correct formula and correct substitution, (A1) for correct answer. (ft) from answer to part (c).[2 marks]
Question
In the diagram below A, B and C represent three villages and the line segments AB, BC and CA represent the roads joining them. The lengths of AC and CB are 10 km and 8 km respectively and the size of the angle between them is 150°.
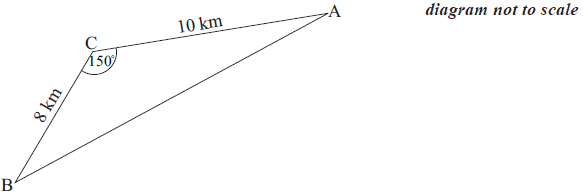
a.Find the length of the road AB.[3]
b.Find the size of the angle CAB.[3]
c.Village D is halfway between A and B. A new road perpendicular to AB and passing through D is built. Let T be the point where this road cuts AC. This information is shown in the diagram below.
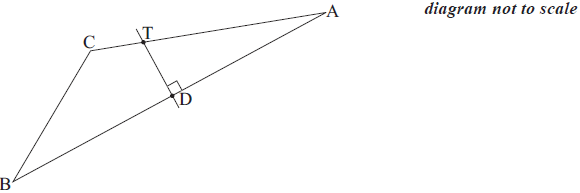
Write down the distance from A to D.[1]
d.Show that the distance from D to T is 2.06 km correct to three significant figures.[2]
e.A bus starts and ends its journey at A taking the route AD to DT to TA.
Find the total distance for this journey.[3]
f.The average speed of the bus while it is moving on the road is 70 km h–1. The bus stops for 5 minutes at each of D and T .
Estimate the time taken by the bus to complete its journey. Give your answer correct to the nearest minute.[4]
▶️Answer/Explanation
Markscheme
AB2 = 102 + 82 – 2 × 10 × 8 × cos150° (M1)(A1)
AB = 17.4 km (A1)(G2)
Note: Award (M1) for substitution into correct formula, (A1) for correct substitution, (A1) for correct answer.[3 marks]
\(\frac{8}{{\sin {\text{C}}\hat {\rm A}{\text{B}}}} = \frac{{17.4}}{{\sin 150^\circ }}\) (M1)(A1)
\({\text{C}}\hat {\rm A}{\text{B}} = 13.3^\circ \) (A1)(ft)(G2)
Notes: Award (M1) for substitution into correct formula, (A1) for correct substitution, (A1) for correct answer. Follow through from their answer to part (a).[3 marks]
AD = 8.70 km (8.7 km) (A1)(ft)
Note: Follow through from their answer to part (a).[1 mark]
DT = tan (13.29…°) × 8.697… = 2.0550… (M1)(A1)
= 2.06 (AG)
Notes: Award (M1) for correct substitution in the correct formula, award (A1) for the unrounded answer seen. If 2.06 not seen award at most (M1)(AO).[2 marks]
\(\sqrt {{{8.70}^2} + {{2.06}^2}} + 8.70 + 2.06\) (A1)(M1)
= 19.7 km (A1)(ft)(G2)
Note: Award (A1) for AT, (M1) for adding the three sides of the triangle ADT, (A1)(ft) for answer. Follow through from their answer to part (c).[3 marks]
\(\frac{{19.7}}{{70}} \times 60 + 10\) (M1)(M1)
= 26.9 (A1)(ft)
Note: Award (M1) for time on road in minutes, (M1) for adding 10, (A1)(ft) for unrounded answer. Follow through from their answer to (e).
= 27 (nearest minute) (A1)(ft)(G3)
Note: Award (A1)(ft) for their unrounded answer given to the nearest minute.[4 marks]
