IB Mathematics SL 3.4 length of an arc area of a sector AI SL Paper 2 - Exam Style Questions - New Syllabus
Question

▶️ Answer/Explanation (Detailed working)
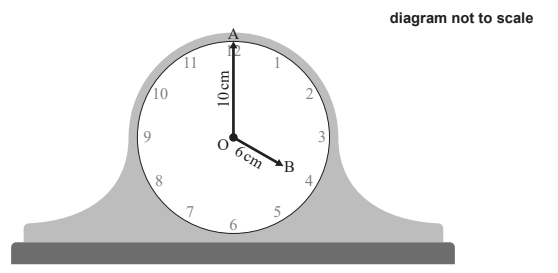
(a) A full turn is \(360^\circ\) and there are 12 hour marks, so each hour mark is \(360^\circ/12=30^\circ\). From 12 to 4 is 4 hour marks: \[ \angle A\widehat{O}B = 4\times 30^\circ=\boxed{120^\circ}. \]
(b) Triangle \(AOB\) has sides \(OA=10\), \(OB=6\), included angle \(120^\circ\). By the cosine rule, \[ AB^2 = 10^2+6^2 – 2(10)(6)\cos 120^\circ = 100+36 -120\left(-\tfrac{1}{2}\right) = 136 + 60 = 196. \] Hence \(AB=\sqrt{196}=\boxed{14\text{ cm}}.\) M1 A1 A1
(c) In 13 minutes, the minute hand turns \[ \theta = \frac{13}{60}\times 360^\circ = \boxed{78^\circ}. \] M1 A1
(d) Arc length formula (degree measure): \( \ell = \dfrac{\theta}{360^\circ}\,2\pi r\). With \(r=10\), \(\theta=78^\circ\), \[ \ell = \frac{78}{360}\cdot 2\pi\cdot 10 = \frac{13}{60}\cdot 20\pi = \frac{13}{3}\pi \approx \boxed{13.6135\text{ cm}}. \] (Exact form \(\frac{13}{3}\pi\) cm.) M1 A1
(e) Sector area (degree measure): \( A = \dfrac{\theta}{360^\circ}\pi r^2\). With \(r=10\), \(\theta=78^\circ\), \[ A = \frac{78}{360}\cdot \pi\cdot 10^2 = \frac{13}{60}\cdot 100\pi = \frac{65}{3}\pi \approx \boxed{68.0678\text{ cm}^2}. \] M1 A1
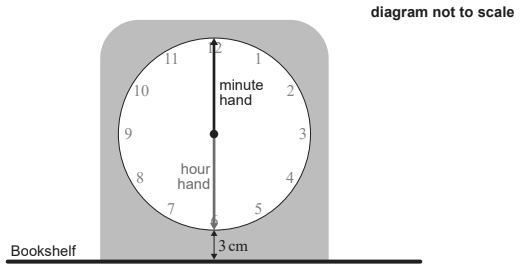
(f) At 6:00, the minute hand points straight up to the top of the circle. The centre of the clock is \(10\) cm above the bottom of the face; since the bottom of the face is 3 cm above the shelf, the centre is \(10+3=13\) cm above the shelf. The minute-hand endpoint is a further \(10\) cm above the centre: \[ \text{height} = 13 + 10 = \boxed{23\text{ cm}}. \]
(g) Substitute \(\theta=160^\circ\) into \(h(\theta)=10\cos\theta+13\): \[ h(160^\circ)=10\cos 160^\circ + 13 = 10\cos(180^\circ-20^\circ)+13 = 10(-\cos 20^\circ)+13 \approx 10(-0.9396926)+13 \approx \boxed{3.60\text{ cm}}. \] M1 A
(h) From \(g(\theta)=-10\cos(\theta/12)+13\), the amplitude is the absolute value of the cosine coefficient: \(\boxed{10}\). A1
(i) The endpoints meet when their heights are equal: \[ h(\theta)=g(\theta) \;\Longrightarrow\; 10\cos\theta+13 = -10\cos\!\Big(\tfrac{\theta}{12}\Big)+13 \;\Longrightarrow\; \cos\theta = -\cos\!\Big(\tfrac{\theta}{12}\Big). \] Using \(-\cos\alpha = \cos(180^\circ-\alpha)\), one solution family is \[ \cos\theta = \cos\!\Big(180^\circ – \tfrac{\theta}{12}\Big) \;\Rightarrow\; \theta = 180^\circ – \tfrac{\theta}{12} + 360^\circ m. \] For the smallest positive \(\theta\) take \(m=0\): \[ \theta + \frac{\theta}{12} = 180^\circ \;\Rightarrow\; \frac{13}{12}\theta = 180^\circ \;\Rightarrow\; \theta = \boxed{\frac{2160^\circ}{13} \;\approx\; 166.15^\circ }. \] (This is the least positive intersection after 6:00.) M1 A1
