Question 2. [Maximum mark: 17]
The diagram below shows a circular clock face with centre O. The clock’s minute hand has a length of 10 cm. The clock’s hour hand has a length of 6 cm.
At 4:00 pm the endpoint of the minute hand is at point A and the endpoint of the hour hand is at point B.
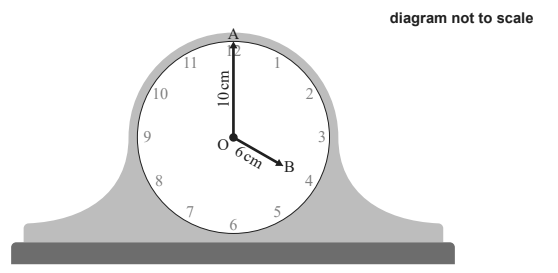
a. Find the size of angle AÔB in degrees. [2]
b. Find the distance between points A and B. [3]
Between 4:00 pm and 4:13 pm, the endpoint of the minute hand rotates through an angle, θ ,
from point A to point C. This is illustrated in the diagram.

c. Find the size of angle θ in degrees. [2]
d. Calculate the length of arc AC. [2]
e. Calculate the area of the shaded sector, AOC. [2]
A second clock is illustrated in the diagram below. The clock face has radius 10 cm with minute and hour hands both of length 10 cm. The time shown is 6:00 am. The bottom of the clock face is located 3 cm above a horizontal bookshelf.
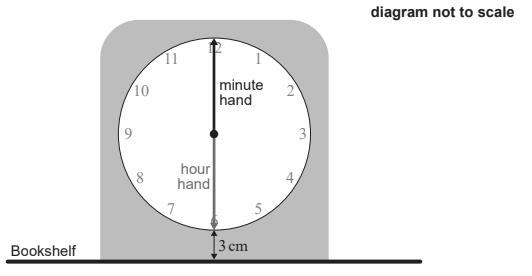
Write down the height of the endpoint of the minute hand above the bookshelf
at 6:00 am. [1]
f. The height, h centimetres, of the endpoint of the minute hand above the bookshelf is modelled by the function
h(θ ) = 10 cosθ + 13 , θ ≥ 0 ,
where θ is the angle rotated by the minute hand from 6:00 am.
g. Find the value of h when θ = 160° . [2]
The height, g centimetres, of the endpoint of the hour hand above the bookshelf is modelled by the function
g(θ ) = -10 cos \((\frac{\Theta }{12})\) + 13 , θ ≥ 0 ,
where θ is the angle in degrees rotated by the minute hand from 6:00 am.
h. Write down the amplitude of g(θ ) . [1]
The endpoints of the minute hand and hour hand meet when θ = k .
Find the smallest possible value of k . [2]
Answer/Explanation
(a) \(4\times \frac{360°\cdot }{12}OR 4\times 30° = 120°\)
(b) cosine rule \(AB^{2}= 10^{2}+6^{2}-2\times 10\times 6\times cos (120°)\)
\(AB= 14cm\)
(c) \(\Theta = 13\times 6= 78°\)
(d) arc length l= \(\frac{78}{360} \times 2\times \pi \times 10\) OR
\(l= \frac{13\pi }{30}\times 10 = 13.6cm(13.6135…,4.33\pi ,\frac{13\pi }{3})\)
(e) Area of a sector \(A= \frac{78}{360}\times \pi \times 10^{2}\) OR \( l=\frac{1}{2}\times \frac{13\pi }{30}\times 10^{2}= 68.1cm^{2}(68.0678…,21.7\pi ,\frac{65\pi }{3}\)
(f) 23
(g) correct substitution h =10cos (160 ) + 13 = 3.60 cm (3.60307…)
(h) 10 (i) EITHER 10\(\times cos(\Theta )+13 = -10\times cos(\frac{\Theta }{12})\)+13
OR  THEN k =196° (196.363…)
THEN k =196° (196.363…)
Question
A sector of a circle, centre O and radius 4.5m, is shown in the following diagram.
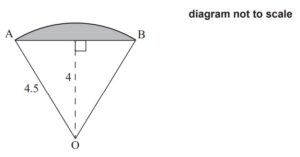
(a) (i) Find the angle AÔB.
(ii) Find the area of the shaded segment. [8]
A square field with side 8m has a goat tied to a post in the centre by a rope such that the
goat can reach all parts of the field up to 4.5m from the post.
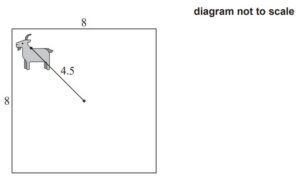
(b) (i) Find the area of a circle with radius 4.5m.
(ii) Find the area of the field that can be reached by the goat. [5]
Let V be the volume of grass eaten by the goat, in cubic metres, and t be the length of time,
in hours, that the goat has been in the field.
The goat eats grass at the rate of \(\frac{dV}{dt}=0.3te^{-t}\).
(c) Find the value of t at which the goat is eating grass at the greatest rate. [2]
Answer/Explanation
Ans
4. (a) (i) \(\left ( \frac{1}{2}A\hat{O}B= \right )\arccos \left ( \frac{4}{4.5} \right )=27.266…\) (M1)(A1)
AOB 54.532… ≈ 54.5 o = ( 0.951764…≈ 0.952 radians) A1
Note: Other methods may be seen; award (M1)(A1) for use of a correct trigonometric
method to find an appropriate angle and then A1 for the correct answer.
(ii) finding area of triangle
EITHER
area of triangle \(=\frac{1}{2}\times 4.5^{2}\times \sin (54.532…)\) (M1)
Note: Award M1 for correct substitution into formula.
= 8.24621…≈ 8.25 m2
OR
\(AB=2\times \sqrt{4.5^{2}-4^{2}}=4.1231…\) (M1)
\(area\ triangle=\frac{4.12131…\times 4}{2}\) (A1)
= 8.24621…≈ 8.25 m2
EITHER
\(area\ of \ sector=\frac{54.532…}{360}\times \pi \times 4.5^{2}\) (M1)
= 9.63661… ≈ 9.64 m2
OR
\(area\ of \ sector=\frac{1}{2}\times 0.9517641.. \times 4.5^{2}\) (M1)
= 9.63661… ≈ 9.64 m2 (A1)
THEN
area of segment = 9.63661… 8.24621… −
=1.39 m2 (1.39040…) A1
[8 marks]
(b) (i) 2 π× 4.5 (M1)
63.6 m2 (63.6172… m2 ) A1
(ii) METHOD 1
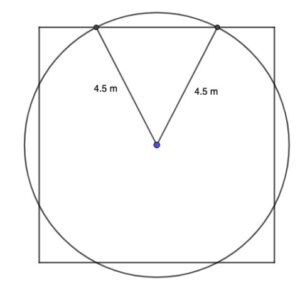
4 1.39040… × (5.56160) (A1)
subtraction of four segments from area of circle (M1)
= 58.1 m2 (58.055…) A1
METHOD 2
\(4(0.5\times 4.5^{2} \times\sin 54.532… )+4\left ( \frac{35.4679}{360}\times\pi \times 4.5^{2} \right )\) (M1)
= 32.9845… + 25.0707 (A1)
= 58.1 m2 (58.055 …) A1
[5 marks]
(c) sketch of \(\frac{dV}{dt}\) OR \(\frac{dV}{dt}=0.110363…\) OR attempt to find where \(\frac{d^{2}V}{dt^{2}}=0\) (M1)
t =1 hour A1
[2 marks]
[Total 15 marks]
Question
The interior of a circle of radius 2 cm is divided into an infinite number of sectors. The areas of these sectors form a geometric sequence with common ratio k. The angle of the first sector is \(\theta \) radians.
(a) Show that \(\theta = 2\pi (1 – k)\).
(b) The perimeter of the third sector is half the perimeter of the first sector.
Find the value of k and of \(\theta \).
Answer/Explanation
Markscheme
(a) the area of the first sector is \(\frac{1}{2}{2^2}\theta \) (A1)
the sequence of areas is \(2\theta ,{\text{ }}2k\theta ,{\text{ }}2{k^2}\theta \ldots \) (A1)
the sum of these areas is \(2\theta (1 + k + {k^2} + \ldots )\) (M1)
\( = \frac{{2\theta }}{{1 – k}} = 4\pi \) M1A1
hence \(\theta = 2\pi (1 – k)\) AG
Note: Accept solutions where candidates deal with angles instead of area.
[5 marks]
(b) the perimeter of the first sector is \(4 + 2\theta \) (A1)
the perimeter of the third sector is \(4 + 2{k^2}\theta \) (A1)
the given condition is \(4 + 2{k^2}\theta = 2 + \theta \) M1
which simplifies to \(2 = \theta (1 – 2{k^2})\) A1
eliminating \(\theta \), obtain cubic in k: \(\pi (1 – k)(1 – 2{k^2}) – 1 = 0\) A1
or equivalent
solve for k = 0.456 and then \(\theta = 3.42\) A1A1
[7 marks]
Total [12 marks]
Examiners report
This was a disappointingly answered question.
Part(a) – Many candidates correctly assumed that the areas of the sectors were proportional to their angles, but did not actually state that fact.
Part(b) – Few candidates seem to know what the term ‘perimeter’ means.
Question
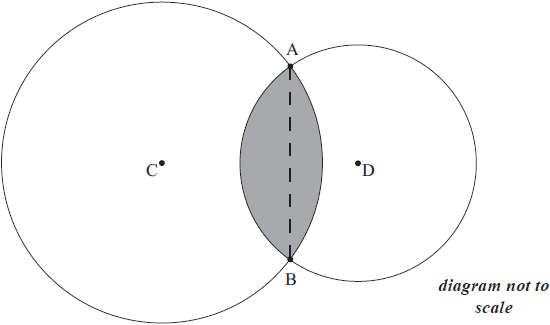
The radius of the circle with centre C is 7 cm and the radius of the circle with centre D is 5 cm. If the length of the chord [AB] is 9 cm, find the area of the shaded region enclosed by the two arcs AB.
Answer/Explanation
Markscheme

\(\alpha = 2\arcsin \left( {\frac{{4.5}}{7}} \right)\) (\( \Rightarrow \alpha = 1.396… = 80.010^\circ …\)) M1(A1)
\(\beta = 2\arcsin \left( {\frac{{4.5}}{5}} \right)\) (\( \Rightarrow \beta = 2.239… = 128.31^\circ …\)) (A1)
Note: Allow use of cosine rule.
area \(P = \frac{1}{2} \times {7^2} \times \left( {\alpha – \sin \alpha } \right) = 10.08…\) M1(A1)
area \(Q = \frac{1}{2} \times {5^2} \times \left( {\beta – \sin \beta } \right) = 18.18…\) (A1)
Note: The M1 is for an attempt at area of sector minus area of triangle.
Note: The use of degrees correctly converted is acceptable.
area = 28.3 (cm2) A1
[7 marks]
Examiners report
Whilst most candidates were able to make the correct construction to solve the problem some candidates seemed unable to find the area of a segment. In a number of cases candidates used degrees in a formula that required radians. There were a number of candidates who followed a completely correct method but due to premature approximation were unable to obtain a correct solution.
