Question
The diagram below shows the graph of a line \(L\) passing through (1, 1) and (2 , 3) and the graph \(P\) of the function \(f (x) = x^2 − 3x − 4\)
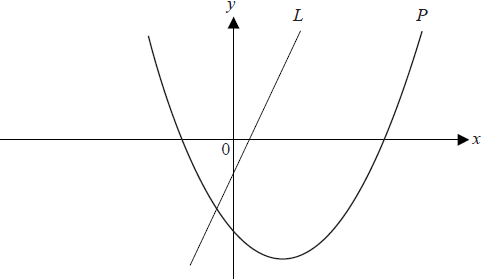
a.Find the gradient of the line L.[2]
b.Differentiate \(f (x)\) .[2]
c.Find the coordinates of the point where the tangent to P is parallel to the line L.[3]
d.Find the coordinates of the point where the tangent to P is perpendicular to the line L.[4]
e.Find
(i) the gradient of the tangent to P at the point with coordinates (2, − 6).
(ii) the equation of the tangent to P at this point.[3]
f.State the equation of the axis of symmetry of P.[1]
g.Find the coordinates of the vertex of P and state the gradient of the curve at this point.[3]
▶️Answer/Explanation
Markscheme
for attempt at substituted \(\frac{{ydistance}}{{xdistance}}\) (M1)
gradient = 2 (A1)(G2)[2 marks]
\(2x – 3\) (A1)(A1)
(A1) for \(2x\) , (A1) for \(-3\)[2 marks]
for their \(2x – 3 =\) their gradient and attempt to solve (M1)
\(x = 2.5\) (A1)(ft)
\(y = -5.25\) ((ft) from their x value) (A1)(ft)(G2)[3 marks]
for seeing \(\frac{{ – 1}}{{their(a)}}\) (M1)
solving \(2x – 3 = – \frac{1}{2}\) (or their value) (M1)
x = 1.25 (A1)(ft)(G1)
y = – 6.1875 (A1)(ft)(G1)[4 marks]
(i) \(2 \times 2 – 3 = 1\) ((ft) from (b)) (A1)(ft)(G1)
(ii) \(y = mx + c\) or equivalent method to find \(c \Rightarrow -6 = 2 + c\) (M1)
\(y = x – 8\) (A1)(ft)(G2)[3 marks]
\(x = 1.5\) (A1)[1 mark]
for substituting their answer to part (f) into the equation of the parabola (1.5, −6.25) accept x = 1.5, y = −6.25 (M1)(A1)(ft)(G2)
gradient is zero (accept \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\)) (A1)[3 marks]
Question
On the coordinate axes below, \({\text{D}}\) is a point on the \(y\)-axis and \({\text{E}}\) is a point on the \(x\)-axis. \({\text{O}}\) is the origin. The equation of the line \({\text{DE}}\) is \(y + \frac{1}{2}x = 4\).
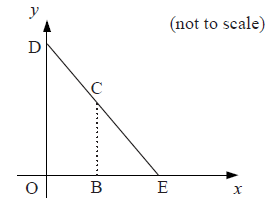
a.Write down the coordinates of point \({\text{E}}\).[2]
b.\({\text{C}}\) is a point on the line \({\text{DE}}\). \({\text{B}}\) is a point on the \(x\)-axis such that \({\text{BC}}\) is parallel to the \(y\)-axis. The \(x\)-coordinate of \({\text{C}}\) is \(t\).
Show that the \(y\)-coordinate of \({\text{C}}\) is \(4 – \frac{1}{2}t\).[2]
c.\({\text{OBCD}}\) is a trapezium. The \(y\)-coordinate of point \({\text{D}}\) is \(4\).
Show that the area of \({\text{OBCD}}\) is \(4t – \frac{1}{4}{t^2}\).[3]
d.The area of \({\text{OBCD}}\) is \(9.75\) square units. Write down a quadratic equation that expresses this information.[1]
e.(i) Using your graphic display calculator, or otherwise, find the two solutions to the quadratic equation written in part (d).
(ii) Hence find the correct value for \(t\). Give a reason for your answer.[4]
▶️Answer/Explanation
Markscheme
\({\text{E}}(8{\text{, }}0)\) (A1)(A1)
Notes: Brackets required but do not penalize again if mark lost in Q4 (i)(d). If missing award (A1)(A0).
Accept \(x = 8\), \(y = 0\)
Award (A1) for \(x = 8\)
\(y + \frac{1}{2}t = 4\) (M1)(M1)
Note: (M1) for the equation of the line seen. (M1) for substituting \(t\).
\(y = 4 – \frac{1}{2}t\) (AG)
Note: Final line must be seen or previous (M1) mark is lost.[2 marks]
\({\text{Area}} = \frac{1}{2} \times (4 + 4 – \frac{1}{2}t) \times t\) (M1)(A1)
Note: (M1) for substituting in correct formula, (A1) for correct substitution.
\( = \frac{1}{2} \times (8 – \frac{1}{2}t) \times t = \frac{1}{2}(8t – \frac{1}{2}{t^2})\) (A1)
\( = 4t – \frac{1}{4}{t^2}\) (AG)
Note: Final line must be seen or previous (A1) mark is lost.[3 marks]
\(4t – \frac{1}{4}{t^2} = 9.75\) or any equivalent form. (A1)[1 mark]
(i) \(t = 3\) or \(t =13\) (A1)(ft)(A1)(ft)(G2)
Note: Follow through from candidate’s equation to part (d). Award (A0)(A1)(ft) for \((3{\text{, }}0)\) and \((13{\text{, }}0)\).
(ii) \(t\) must be a value between \(0\) and \(8\) then \(t = 3\)
Note: Accept \({\text{B}}\) is between \({\text{O}}\) and \({\text{E}}\). Do not award (R0)(A1).
Question
Consider the curve \(y = {x^3} + \frac{3}{2}{x^2} – 6x – 2\) .
a.(i) Write down the value of \(y\) when \(x\) is \(2\).
(ii) Write down the coordinates of the point where the curve intercepts the \(y\)-axis.[3]
b.Sketch the curve for \( – 4 \leqslant x \leqslant 3\) and \( – 10 \leqslant y \leqslant 10\). Indicate clearly the information found in (a).[4]
c.Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) .[3]
d.Let \({L_1}\) be the tangent to the curve at \(x = 2\).
Let \({L_2}\) be a tangent to the curve, parallel to \({L_1}\).
(i) Show that the gradient of \({L_1}\) is \(12\).
(ii) Find the \(x\)-coordinate of the point at which \({L_2}\) and the curve meet.
(iii) Sketch and label \({L_1}\) and \({L_2}\) on the diagram drawn in (b).[8]
e.It is known that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} > 0\) for \(x < – 2\) and \(x > b\) where \(b\) is positive.
(i) Using your graphic display calculator, or otherwise, find the value of \(b\).
(ii) Describe the behaviour of the curve in the interval \( – 2 < x < b\) .
(iii) Write down the equation of the tangent to the curve at \(x = – 2\).[5]
▶️Answer/Explanation
Markscheme
(i) \(y = 0\) (A1)
(ii) \((0{\text{, }}{- 2})\) (A1)(A1)
Note: Award (A1)(A0) if brackets missing.
OR
\(x = 0{\text{, }}y = – 2\) (A1)(A1)
Note: If coordinates reversed award (A0)(A1)(ft). Two coordinates must be given.[3 marks]
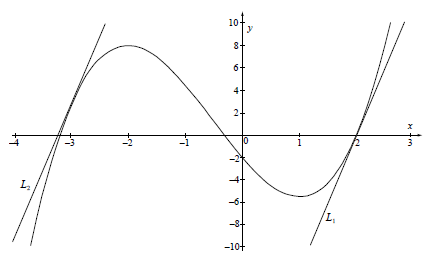 (A4)
(A4)
Notes: (A1) for appropriate window. Some indication of scale on the \(x\)-axis must be present (for example ticks). Labels not required. (A1) for smooth curve and shape, (A1) for maximum and minimum in approximately correct position, (A1) for \(x\) and \(y\) intercepts found in (a) in approximately correct position.[4 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 3{x^2} + 3x – 6\) (A1)(A1)(A1)
Note: (A1) for each correct term. Award (A1)(A1)(A0) at most if any other term is present.[3 marks]
(i) \(3 \times 4 + 3 \times 2 – 6 = 12\) (M1)(A1)(AG)
Note: (M1) for using the derivative and substituting \(x = 2\) . (A1) for correct (and clear) substitution. The \(12\) must be seen.
(ii) Gradient of \({L_2}\) is \(12\) (can be implied) (A1)
\(3{x^2} + 3x – 6 = 12\) (M1)
\(x = – 3\) (A1)(G2)
Note: (M1) for equating the derivative to \(12\) or showing a sketch of the derivative together with a line at \(y = 12\) or a table of values showing the \(12\) in the derivative column.
(iii) (A1) for \({L_1}\) correctly drawn at approx the correct point (A1)
(A1) for \({L_2}\) correctly drawn at approx the correct point (A1)
(A1) for 2 parallel lines (A1)
Note: If lines are not labelled award at most (A1)(A1)(A0). Do not accept 2 horizontal or 2 vertical parallel lines.[8 marks]
(i) \(b = 1\) (G2)
(ii) The curve is decreasing. (A1)
Note: Accept any valid description.
(iii) \(y = 8\) (A1)(A1)(G2)
Note: (A1) for “\(y =\) a constant”, (A1) for \(8\).[5 marks]
Question
The vertices of quadrilateral ABCD as shown in the diagram are A (3, 1), B (0, 2), C (–2, 1) and D (–1, –1).
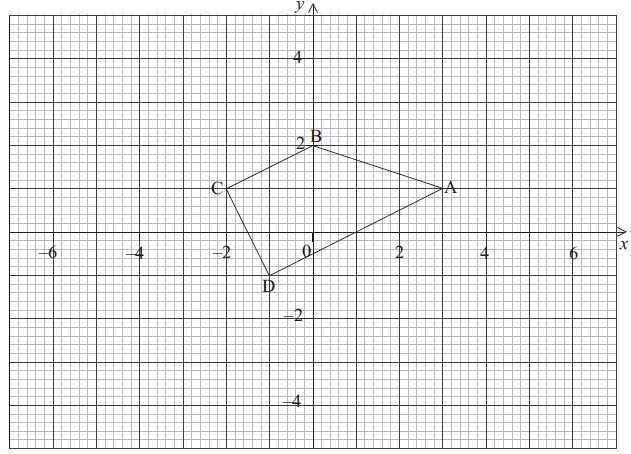
a.Calculate the gradient of line CD.[2]
b.Show that line AD is perpendicular to line CD.[2]
c.Find the equation of line CD. Give your answer in the form \(ax + by = c\) where \(a,{\text{ }}b,{\text{ }}c \in \mathbb{Z}\).[3]
d.Lines AB and CD intersect at point E. The equation of line AB is \(x + 3y = 6\).
Find the coordinates of E.[2]
e.Lines AB and CD intersect at point E. The equation of line AB is \(x + 3y = 6\).
Find the distance between A and D.[2]
f.The distance between D and E is \(\sqrt{20}\).
Find the area of triangle ADE.[2]
▶️Answer/Explanation
Markscheme
\({\text{Gradient of CD}} = \frac{{1 – ( – 1)}}{{ – 2 – ( – 1)}}\) (M1)
\( = – 2\) (A1)(G2)
Note: Award (M1) for correct substitution in gradient formula.[2 marks]
\({\text{Gradient of AD}} = \frac{1}{2}\) (A1)
\( – 2 \times \frac{1}{2} = – 1\) or \(\frac{1}{2}\) is negative reciprocal of –2 (M1)
Hence AD is perpendicular for CD. (AG)
Note: Last line must be seen for the (M1) to be awarded.[2 marks]
\(y = -2x – 3\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for their (a), (A1)(ft) for –3.
If part (a) incorrect award (A1)(ft) for their y-intercept only if working is seen.
OR
\(y – 1 = -2(x + 2)\) (A1)(ft)(A1)
OR
\(y + 1 = -2(x + 1)\) (A1)(ft)(A1)
Note: Award (A1)(ft) for their (a), (A1) for correct substitution of point.
\(2x + y = -3\) (A1)(ft)
Note: The final (A1)(ft) is for their equation in the stated form.[3 marks]
E (−3, 3) (Accept x = −3, y = 3) (G2)
OR
Award (M1) for solving the pair of simultaneous equations by hand. (A1)(ft) for correct answer, (ft) from their (c). (M1)(A1)(ft)
OR
Award (M1) for having extended the lines in their own graph seen drawn on answer paper. (A1) for correct answer. (M1)(A1)
Note: Missing coordinate brackets receive (G1)(G0) or (M1)(A0).[2 marks]
Distance between A and D = \(\sqrt {4^2 + 2^2}\) (M1)
\( = \sqrt{20}\) OR \(2 \sqrt {5}\) OR 4.47 (3 s.f.) (A1)(G2)
Note: Award (M1) for correct substitution into the distance formula, (A1) for correct answer.[2 marks]
Area of ADE = \(\frac{1}{2}\sqrt {20} \times \sqrt {20} \) (M1)
= 10 (A1)(ft)(G2)
Follow through from (e).[2 marks]
