IB DP Math AI: Topic SL 5.11: Indefinite integral: IB style Questions HL Paper 2

Ans:

(a)

\(\frac{1}{x(k-x)}= \frac{a}{x}+ \frac{b}{k-x}\) 

a (k-x)+ bx = 1 

attempt to compare coefficients OR substitute x = k  and  x = o and solve

a = \(\frac{1}{k} \) and \( b = \frac{1}{k }\)

\(f ‘(x)= \frac{1}{kx}+ \frac{1}{k(k-x)}\)

(b)

attempt to integrate their \(\frac{a}{x}+ \frac{b}{k-x}\)

\(f(x)=\frac{1}{k}\int (\frac{1}{x}+ \frac{1}{k-x})dx\)

= \(\frac{1}{k}(ln |x| – ln | k-x |)+c\)

\(\frac{1}{k}ln |\frac{x}{k-x}|+c\)

(c) attempt to separate variables and integrate both sides

5k \(\int \frac{1}{p(k-p)}dp = \int 1 dt\)

5 (ln p – ln (k-P))= t+ c

EITHER 

attempt to substitute t = o , P = 1200 into an equation involving c

c= 5( ln 1200 – ln (k-1200))

= 5ln \(\frac{1200}{k-1200}\)

5 (ln p- ln (k-p ))= t+5 \((ln 1200-ln (k-1200))\)

\(ln (\frac{p(k-1200)}{1200(k-p)})=\frac{t}{5}\)

\(\frac{p(k-1200)}{1200(k-p)}= e ^{^{\frac{t}{5}}}\)

OR

ln \(\frac{p}{k-p}= \frac{t+ c }{5 }\)

\(\frac{p }{k-p }= Ae ^{\frac{t}{5}}\)

attempt to substitute t = 0, p = 1200

\(\frac{1200}{k-1200}= A\)

\(\frac{p }{k-p }= \frac{1200 e^{\frac{t}{5}}}{k- 1200}\)

THEN

attempt to rearrange and isolate  p

\(pk – 1200p = 1200ke ^{\frac{t}{5}}- 1200 pe ^{\frac{t}{5 }}\)

OR \(pke ^{\frac{-t}{5}}-1200pe^{\frac{-t}{5}}= 1200k – 1200p\)

OR

\(\frac{K}{P}-1 = \frac{K-1200}{1200e^{\frac{t}{5}}} \)

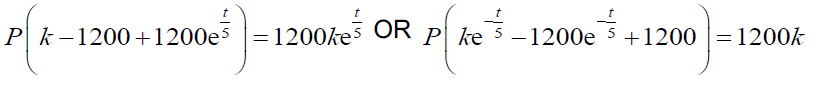
p = \(\frac{1200k}{(k-1200)e ^{\frac{t}{5}}+1200}\)

(d)

attempt to substitute t = 10 p = 2400

2400=\(\frac{1200k}{(k-1200)e^{-2}+ 1200 }\)

k = 2845.34..

k= 2845

(e)

attempt to find the maximum of the first derivative graph OR zero of the second derivative graph OR that p =\(\frac{k}{2}(=1422.67..)\)

t =1.57814…

=1.58 (days)