Question
Consider the curve \(y = \sqrt{x}\).
(a) (i) Find \(\frac{dy}{dx}\).
(ii) Hence show that the equation of the tangent to the curve at the point (0.16, 0.4) is y = 1.25x + 0.2.
The shape of a piece of metal can be modelled by the region bounded by the functions f , g,
the x-axis and the line segment [AB], as shown in the following diagram. The units on the x
and y axes are measured in metres.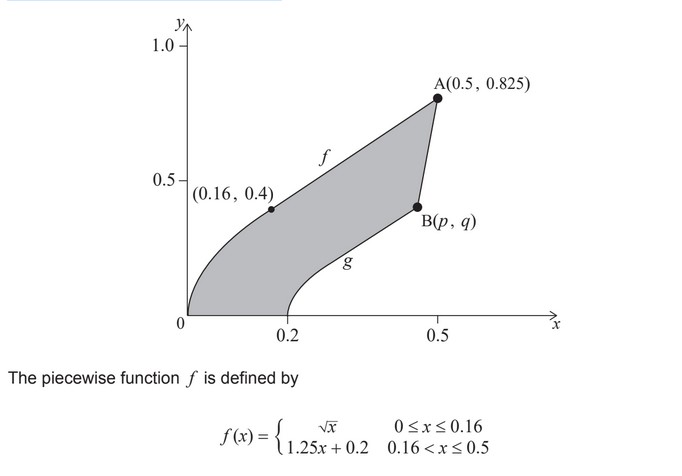
The graph of g is obtained from the graph of f by:
- a sketch scale factor of \(\frac{1}{2}\) in the x direction,
- followed by a stretch scale factor \(\frac{1}{2}\) in the y direction,
- followed by a translation of 0.2 units to the right.
Point A lies on the graph of f and has coordinates (0.5, 0.825). Point B is the image of A
under the given transformations and has coordinates (p , q).
(b) Find the value of p and the value of q.
The piecewise function g is given by
\(g(x)=\left\{\begin{matrix}
h(x) & 0.2 \leq x \leq a\\
1.25x + b & a<x \leq p
\end{matrix}\right.\)
(c) Find
(i) an expression for h(x).
(ii) the value of a.
(iii) the value of b.
(d) (i) Find the area enclosed by y = f (x), the x-axis and the line x = 0.5.
The area enclosed by y = g(x), the x-axis and the line x = p is 0.0627292 \(m^2\) correct to six significant figures.
(ii) Find the area of the shaded region on the diagram.
▶️Answer/Explanation
Ans:
(a) (i) \(y=x^{\frac{1}{2}}\)
\(\frac{dy}{dx}=\frac{1}{2} x^{-\frac{1}{2}}\)
(ii) gradient at x = 0.16 is \(\frac{1}{2} \times \frac{1}{\sqrt{0.16}}\)
= 1.25
EITHER
y – 0.4 = 1.25 (x – 0.16)
OR
0.4 = 1.25(0.16) + b
THEN
hence y = 1.25x + 0.2
(b) p q = = 0.45, 0.4125 ( 0.413) or (accept “(0.45, 0.4125)”)
(c) (i) \((h(x)=) \frac{1}{2} \sqrt{2(x-0.2)}\)
(ii) (a=) 0.28
(iii) EITHER
correct substitution of their part (b) (or (0.28, 0.2)) into the given expression
OR
\(\frac{1}{2}(1.25 \times 2 (x – 0.2)+0.2)\)
THEN
(b=) – 0.15
(d) (i) recognizing need to add two integrals
\(\int_{0}^{0.16} \sqrt{x}dx + \int_{0.16}^{0.5}(1.25x + 0.2)dx\)
0.251 \(m^2\) (0.250916…)
(ii) EITHER
area of trapezoid \(\frac{1}{2} \times 0.05(0.4125 + 0.825) = 0.0309375\)
OR
\(\int_{0.45}^{0.5}(8.25x – 3.3)dx = 0.0309375\)
THEN
shaded area = 0.250916… – 0.627292 – 0.0309375
= 0.157 \(m^2\) (0.15725)
Question
By using the substitution \(x = 2\tan u\), show that \(\int {\frac{{{\text{d}}x}}{{{x^2}\sqrt {{x^2} + 4} }} = \frac{{ – \sqrt {{x^2} + 4} }}{{4x}} + C} \).
▶️Answer/Explanation
Markscheme
EITHER
\(\frac{{{\text{d}}x}}{{{\text{d}}u}} = 2\,{\text{se}}{{\text{c}}^2}u\) A1
\(\int {\frac{{2\,{\text{se}}{{\text{c}}^2}u{\text{d}}u}}{{4{{\tan }^2}u\sqrt {4 + 4{{\tan }^2}u} }}} \) (M1)
\(\int {\frac{{2\,{\text{se}}{{\text{c}}^2}u{\text{d}}u}}{{4{{\tan }^2}u \times 2\,\sec u}}} \) \(( = \int {\frac{{{\text{d}}u}}{{4{{\sin }^2}u\sqrt {{{\tan }^2}u + 1} }}{\text{ or }} = \int {\frac{{2\,{\text{se}}{{\text{c}}^2}u{\text{d}}u}}{{4{{\tan }^2}u\sqrt {4{{\sec }^2}u} }})} } \) A1
OR
\(u = \arctan \frac{x}{2}\)
\(\frac{{{\text{d}}u}}{{{\text{d}}x}} = \frac{2}{{{x^2} + 4}}\) A1
\(\int {\frac{{\sqrt {4{{\tan }^2}u + 4{\text{d}}u} }}{{2 \times 4{{\tan }^2}u}}} \) (M1)
\(\int {\frac{{2\,\sec u{\text{d}}u}}{{2 \times 4{{\tan }^2}u}}} \) A1
THEN
\( = \frac{1}{4}\int {\frac{{\sec u{\text{d}}u}}{{{{\tan }^2}u}}} \)
\( = \frac{1}{4}\int {{\text{cosec}}\,u\cot u{\text{d}}u{\text{ }}\left( { = \frac{1}{4}\int {\frac{{\cos u}}{{{{\sin }^2}u}}{\text{d}}u} } \right)} \) A1
\( = – \frac{1}{4}{\text{cosec}}\,u( + C){\text{ }}\left( { = – \frac{1}{{4\sin u}}( + C)} \right)\) A1
use of either \(u = \frac{x}{2}\) or an appropriate trigonometric identity M1
either \(\sin u = \frac{x}{{\sqrt {{x^2} + 4} }}\) or \({\text{cosec}}\,u = \frac{{\sqrt {{x^2} + 4} }}{x}\) (or equivalent) A1
\( = \frac{{ – \sqrt {{x^2} + 4} }}{{4x}}( + C)\) AG
[7 marks]
Examiners report
Most candidates found this a challenging question. A large majority of candidates were able to change variable from x to u but were not able to make any further progress.
Question
a.Given that \(2{x^3} – 3x + 1\) can be expressed in the form \(Ax\left( {{x^2} + 1} \right) + Bx + C\), find the values of the constants \(A\), \(B\) and \(C\).[2]
b.Hence find \(\int {\frac{{2{x^3} – 3x + 1}}{{{x^2} + 1}}} {\text{d}}x\).[5]
▶️Answer/Explanation
Markscheme
\(2{x^3} – 3x + 1 = Ax\left( {{x^2} + 1} \right) + Bx + C\)
\(A = 2,\,\,C = 1,\) A1
\(A + B = – 3 \Rightarrow B = – 5\) A1
[2 marks]
\(\int {\frac{{2{x^3} – 3x + 1}}{{{x^2} + 1}}} {\text{d}}x = \int {\left( {2x – \frac{{5x}}{{{x^2} + 1}} + \frac{1}{{{x^2} + 1}}} \right)} {\text{d}}x\) M1M1
Note: Award M1 for dividing by \(\left( {{x^2} + 1} \right)\) to get \(2x\), M1 for separating the \(5x\) and 1.
\( = {x^2} – \frac{5}{2}{\text{ln}}\left( {{x^2} + 1} \right) + {\text{arctan}}\,x\left( { + c} \right)\) (M1)A1A1
Note: Award (M1)A1 for integrating \({\frac{{5x}}{{{x^2} + 1}}}\), A1 for the other two terms.
[5 marks]
Examiners report
[N/A]
[N/A]
