IB Mathematics SL 5.7 Optimization problems in context AI SL Paper 2 - Exam Style Questions - New Syllabus
Question
▶️ Answer / Explanation
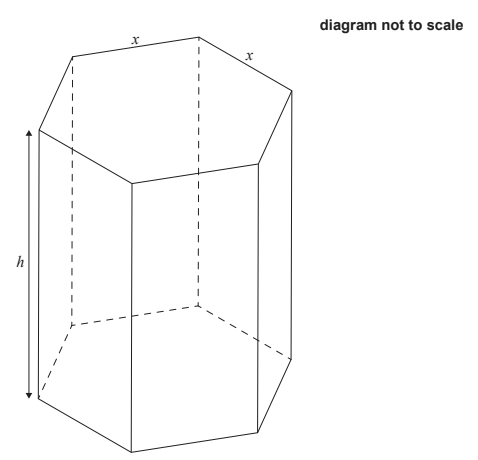
(a) A regular hexagon can be split into 6 equilateral triangles of side \(x\).
Area of one: \( \dfrac12 x^2\sin 60^\circ=\dfrac12 x^2\cdot\dfrac{\sqrt3}{2}=\dfrac{\sqrt3}{4}x^2\).
So base area: \( A_{\text{hex}}=6\cdot\dfrac{\sqrt3}{4}x^2=\boxed{\dfrac{3\sqrt3}{2}\,x^2}. \)
(b) External surface area \(S\) = two hexagonal ends \(+\) lateral area: \[ S = 2A_{\text{hex}}+(\text{perimeter})\cdot h = 2\left(\frac{3\sqrt3}{2}x^2\right) + (6x)h = 3\sqrt3\,x^2+6xh. \] Given \(S=1200\): \[ 3\sqrt3\,x^2+6xh=1200\quad\Rightarrow\quad 6xh=1200-3\sqrt3\,x^2 \Rightarrow\boxed{\,h=\frac{200}{x}-\frac{\sqrt3}{2}x\,}. \] Volume \(V = A_{\text{hex}}\cdot h\): \[ V(x)=\left(\frac{3\sqrt3}{2}x^2\right)\!\left(\frac{200}{x}-\frac{\sqrt3}{2}x\right) = 300\sqrt3\,x-\frac{9}{4}x^3 = \boxed{300\sqrt3\,x-\frac{9}{4}x^3}. \]
(c) For \(V(x)=x\!\left(300\sqrt3-\dfrac{9}{4}x^2\right)\):
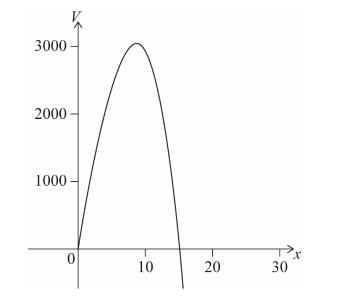
• Intercepts: \(x=0\) and from \(300\sqrt3-\dfrac{9}{4}x^2=0\Rightarrow x=\sqrt{\dfrac{1200\sqrt3}{9}}\approx\boxed{15.20}\).
• Shape: rises from \(V(0)=0\) to a single maximum then decreases to \(V(15.20)\approx0\).
(d) \[ \frac{dV}{dx} = 300\sqrt3 – \frac{27}{4}x^2. \]
(e) Maximize \(V\) by solving \(\dfrac{dV}{dx}=0\): \[ 300\sqrt3-\frac{27}{4}x^2=0 \;\Rightarrow\; x^2=\frac{1200\sqrt3}{27}=\frac{400\sqrt3}{9} \;\Rightarrow\; \boxed{x\approx 8.774\text{ cm}}. \] Check: \(V”(x)=-\dfrac{27}{2}x<0\) for \(x>0\Rightarrow\) maximum.
(f) Maximum volume: \[ V_{\max}=V(8.77382\ldots)=300\sqrt3\,(8.77382\ldots)-\frac{9}{4}(8.77382\ldots)^3 \approx \boxed{3.04\times 10^3\ \text{cm}^3}\ (\text{more precisely } \approx 3039.34\text{ cm}^3). \]
(g) The estimate “(box volume) ÷ (one sphere volume)” assumes perfect packing and zero wall thickness. In reality, spheres leave gaps (they don’t tessellate to fill space) and the box walls occupy volume, so this method overestimates how many Candys fit.
