Question 5. [Maximum mark: 15]
A hollow chocolate box is manufactured in the form of a right prism with a regular hexagonal base. The height of the prism is h cm, and the top and base of the prism have sides of length x cm.
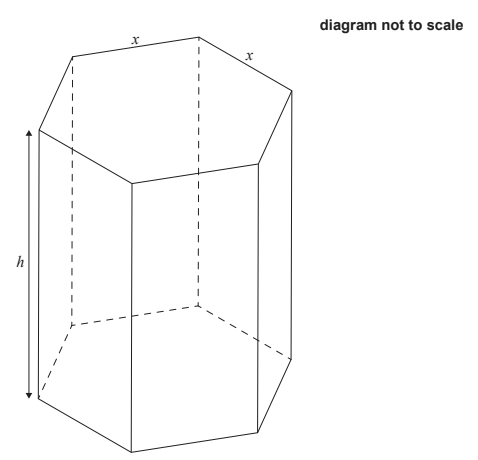
a. Given that \(sin 60\frac{\sqrt{3}}{2}\) show that the area of the base of the box is equal to \(\frac{3\sqrt{3x^{2}}}{2}\) [2]
b. Given that the total external surface area of the box is 1200 cm2, show that the volume of the box may be expressed as V = 300 \(\sqrt{3x}-\frac{9}{4}x^{3}\) [5]
c. Sketch the graph of V = 300 \(\sqrt{3x}-\frac{9}{4}x^{3}\) for 0 ≤ x ≤ 16. [2]
d. Find an expression for \(\frac{dV}{dx}\) . [2]
e. Find the value of x which maximizes the volume of the box. [2]
f. Hence, or otherwise, find the maximum possible volume of the box. [2]
The box will contain spherical chocolates. The production manager assumes that they can calculate the exact number of chocolates in each box by dividing the volume of the box by
the volume of a single chocolate and then rounding down to the nearest integer.
(g) Explain why the production manager is incorrect.[1]
Answer/Explanation
(a) splitting diagram into equilateral triangles area \(= 6(\frac{1}{2}x^{2}sin60)\)
\(=\frac{3\sqrt{3}x^{2}}{2}\)
(b) total surface area of prism
\(1200= 2 (3x^{2}\frac{\sqrt{3}}{2})+6xh\)
\(h= \frac{400-\sqrt{3x^{2}}}{2x}\)
\(volume of prism =\frac{3\sqrt{3}}{2}x^{2}h\)
\(= \frac{3\sqrt{3}}{2}x^{2}(\frac{400-\sqrt{3x^{2}}}{2x})
\(= 300\sqrt{3x}-\frac{9}{4}x^{3}\)
(c) 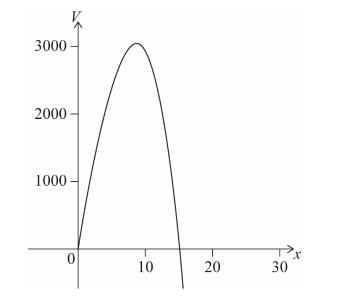
(d)\(\frac{dV}{dx}= 300\sqrt{3}-\frac{27}{4}x^{2}\)
(e) from the graph of V or\(\frac{dV}{dx}OR solving \frac{dV}{dx}= 0\) \( x = 8.77 (8.77382…)\)
(f) from the graph of V OR substituting their value for x into V
\(V_{max}= 3040 cm^{2}\rightarrow (3039.34…)\)
(g) EITHER
wasted space / spheres do not pack densely (tesselate) A1
OR
the model uses exterior values / assumes infinite thinness of materials and
hence the modelled volume is not the true volume
Question 5. [Maximum mark: 16]
The cross-sectional view of a tunnel is shown on the axes below. The line [AB] represents a vertical wall located at the left side of the tunnel.
The height, in metres, of the tunnel above the horizontal ground is modelled by y = -0.1x 3 + 0.8x 2 , 2 ≤ x ≤ 8, , relative to an origin O.
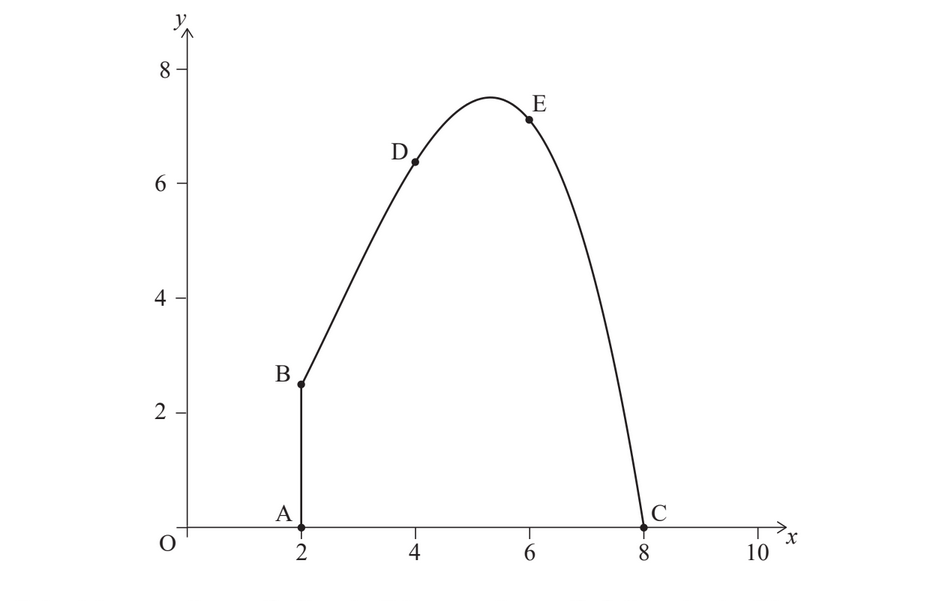
Point A has coordinates (2 , 0), point B has coordinates (2 , 2.4), and point C has coordinates (8 , 0).
a. (i) Find \(\frac{dy}{dx}\)
(ii) Hence find the maximum height of the tunnel. [6]
When x = 4 the height of the tunnel is 6.4 m and when x = 6 the height of the tunnel is 7.2 m. These points are shown as D and E on the diagram, respectively.
b. Use the trapezoidal rule, with three intervals, to estimate the cross-sectional area of the tunnel. [3]
c . (i) Write down the integral which can be used to find the cross-sectional area of the tunnel.
(ii) Hence find the cross-sectional area of the tunnel. [4]
Answer/Explanation
(a) (i) \(\frac{dy}{dx}\)= \(-0.3x^{2}\)+ 1.6x
(ii) \(-0.3x^{2}\)+ 1.6x = 0 x = 5.33 (5.3333… \(\frac{16}{3 })\) \(y = -0.1 5.3333…. + 0.8 5.3333….7.59 m (7.58519…)\)
(b) \(A = \frac{1}{2}\times 2((2.4+0)+2(6.4+7.2))\)= 29 m2
(c)(i) \(A = \int ^{8}_{2}-0.1x^{3}+ 0.8x^{2}dx\) OR
\(A = \int ^{8}_{2}\)ydx
(ii) \(A = 32.4 m^{2}\)
Question
The following diagram shows a semicircle centre O, diameter [AB], with radius 2.
Let P be a point on the circumference, with \({\rm{P}}\widehat {\rm{O}}{\rm{B}} = \theta \) radians.
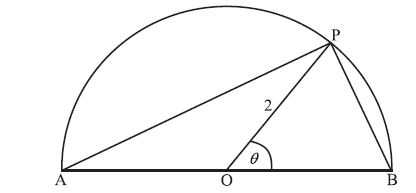
Let S be the total area of the two segments shaded in the diagram below.
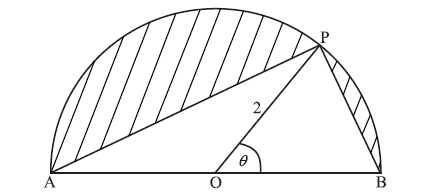
Find the area of the triangle OPB, in terms of \(\theta \) .
Explain why the area of triangle OPA is the same as the area triangle OPB.
Show that \(S = 2(\pi – 2\sin \theta )\) .
Find the value of \(\theta \) when S is a local minimum, justifying that it is a minimum.
Find a value of \(\theta \) for which S has its greatest value.
Answer/Explanation
Markscheme
evidence of using area of a triangle (M1)
e.g. \(A = \frac{1}{2} \times 2 \times 2 \times \sin \theta \)
\(A = 2\sin \theta \) A1 N2
[2 marks]
METHOD 1
\({\rm{P}}\widehat {\rm{O}}{\rm{A = }}\pi – \theta \) (A1)
\({\text{area }}\Delta {\rm{OPA}} = \frac{1}{2}2 \times 2 \times \sin (\pi – \theta )\) \(( = 2\sin (\pi – \theta ))\) A1
since \(\sin (\pi – \theta ) = \sin \theta \) R1
then both triangles have the same area AG N0
METHOD 2
triangle OPA has the same height and the same base as triangle OPB R3
then both triangles have the same area AG N0
[3 marks]
area semicircle \( = \frac{1}{2} \times \pi {(2)^2}\) \(( = 2\pi )\) A1
\({\text{area }}\Delta {\rm{APB}} = 2\sin \theta + 2\sin \theta \) \(( = 4\sin \theta )\) A1
\(S{\text{ = area of semicircle}} – {\text{area }}\Delta {\rm{APB}}\) \(( = 2\pi – 4\sin \theta )\) M1
\(S = 2(\pi – 2\sin \theta )\) AG N0
[3 marks]
METHOD 1
attempt to differentiate (M1)
e.g. \(\frac{{{\rm{d}}S}}{{{\rm{d}}\theta }} = – 4\cos \theta \)
setting derivative equal to 0 (M1)
correct equation A1
e.g. \( – 4\cos \theta = 0\) , \(\cos \theta = 0\) , \(4\cos \theta = 0\)
\(\theta = \frac{\pi }{2}\) A1 N3
EITHER
evidence of using second derivative (M1)
\(S”(\theta ) = 4\sin \theta \) A1
\(S”\left( {\frac{\pi }{2}} \right) = 4\) A1
it is a minimum because \(S”\left( {\frac{\pi }{2}} \right) > 0\) R1 N0
OR
evidence of using first derivative (M1)
for \(\theta < \frac{\pi }{2},S'(\theta ) < 0\) (may use diagram) A1
for \(\theta > \frac{\pi }{2},S'(\theta ) > 0\) (may use diagram) A1
it is a minimum since the derivative goes from negative to positive R1 N0
METHOD 2
\(2\pi – 4\sin \theta \) is minimum when \(4\sin \theta \) is a maximum R3
\(4\sin \theta \) is a maximum when \(\sin \theta = 1\) (A2)
\(\theta = \frac{\pi }{2}\) A3 N3
[8 marks]
S is greatest when \(4\sin \theta \) is smallest (or equivalent) (R1)
\(\theta = 0\) (or \(\pi \) ) A1 N2
[2 marks]
Question
A rectangle is inscribed in a circle of radius 3 cm and centre O, as shown below.
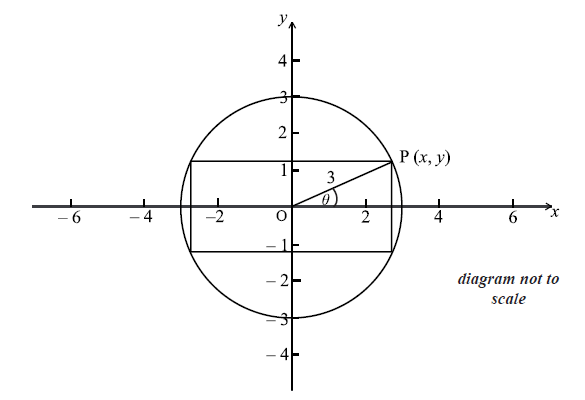
The point P(x , y) is a vertex of the rectangle and also lies on the circle. The angle between (OP) and the x-axis is \(\theta \) radians, where \(0 \le \theta \le \frac{\pi }{2}\) .
Write down an expression in terms of \(\theta \) for
(i) \(x\) ;
(ii) \(y\) .
Let the area of the rectangle be A.
Show that \(A = 18\sin 2\theta \) .
(i) Find \(\frac{{{\rm{d}}A}}{{{\rm{d}}\theta }}\) .
(ii) Hence, find the exact value of \(\theta \) which maximizes the area of the rectangle.
(iii) Use the second derivative to justify that this value of \(\theta \) does give a maximum.
Answer/Explanation
Markscheme
(i) \(x = 3\cos \theta \) A1 N1
(ii) \(y = 3\sin \theta \) A1 N1
[2 marks]
finding area (M1)
e.g. \(A = 2x \times 2y\) , \(A = 8 \times \frac{1}{2}bh\)
substituting A1
e.g. \(A = 4 \times 3\sin \theta \times 3\cos \theta \) , \(8 \times \frac{1}{2} \times 3\cos \theta \times 3\sin \theta \)
\(A = 18(2\sin \theta \cos \theta )\) A1
\(A = 18\sin 2\theta \) AG N0
[3 marks]
(i) \(\frac{{{\rm{d}}A}}{{{\rm{d}}\theta }} = 36\cos 2\theta \) A2 N2
(ii) for setting derivative equal to 0 (M1)
e.g. \(36\cos 2\theta = 0\) , \(\frac{{{\rm{d}}A}}{{{\rm{d}}\theta }} = 0\)
\(2\theta = \frac{\pi }{2}\) (A1)
\(\theta = \frac{\pi }{4}\) A1 N2
(iii) valid reason (seen anywhere) R1
e.g. at \(\frac{\pi }{4}\), \(\frac{{{{\rm{d}}^2}A}}{{{\rm{d}}{\theta ^2}}} < 0\) ; maximum when \(f”(x) < 0\)
finding second derivative \(\frac{{{{\rm{d}}^2}A}}{{{\rm{d}}{\theta ^2}}} = – 72\sin 2\theta \) A1
evidence of substituting \(\frac{\pi }{4}\) M1
e.g. \( – 72\sin \left( {2 \times \frac{\pi }{4}} \right)\) , \( – 72\sin \left( {\frac{\pi }{2}} \right)\) , \( – 72\)
\(\theta = \frac{\pi }{4}\) produces the maximum area AG N0
[8 marks]
Question
Let \({L_x}\) be a family of lines with equation given by \(r\) \( = \left( {\begin{array}{*{20}{c}} x \\ {\frac{2}{x}} \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} {{x^2}} \\ { – 2} \end{array}} \right)\), where \(x > 0\).
Write down the equation of \({L_1}\).
A line \({L_a}\) crosses the \(y\)-axis at a point \(P\).
Show that \(P\) has coordinates \(\left( {0,{\text{ }}\frac{4}{a}} \right)\).
The line \({L_a}\) crosses the \(x\)-axis at \({\text{Q}}(2a,{\text{ }}0)\). Let \(d = {\text{P}}{{\text{Q}}^2}\).
Show that \(d = 4{a^2} + \frac{{16}}{{{a^2}}}\).
There is a minimum value for \(d\). Find the value of \(a\) that gives this minimum value.
Answer/Explanation
Markscheme
attempt to substitute \(x = 1\) (M1)
eg\(\;\;\;\)r \( = \left( {\begin{array}{*{20}{c}} 1 \\ {\frac{2}{1}} \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} {{1^2}} \\ { – 2} \end{array}} \right),{\text{ }}{L_1} = \left( {\begin{array}{*{20}{c}} 1 \\ 2 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 1 \\ { – 2} \end{array}} \right)\)
correct equation (vector or Cartesian, but do not accept “\({L_1}\)”)
eg\(\;\;\;\)r \( = \left( {\begin{array}{*{20}{c}} 1 \\ 2 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 1 \\ { – 2} \end{array}} \right),{\text{ }}y = – 2x + 4\;\;\;\)(must be an equation) A1 N2
[2 marks]
appropriate approach (M1)
eg\(\;\;\;\left( {\begin{array}{*{20}{c}} 0 \\ y \end{array}} \right) = \left( {\begin{array}{*{20}{c}} a \\ {\frac{2}{a}} \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} {{a^2}} \\ { – 2} \end{array}} \right)\)
correct equation for \(x\)-coordinate A1
eg\(\;\;\;0 = a + t{a^2}\)
\(t = \frac{{ – 1}}{a}\) A1
substituting their parameter to find \(y\) (M1)
eg\(\;\;\;y = \frac{2}{a} – 2\left( {\frac{{ – 1}}{a}} \right),{\text{ }}\left( {\begin{array}{*{20}{c}} a \\ {\frac{2}{a}} \end{array}} \right) – \frac{1}{a}\left( {\begin{array}{*{20}{c}} {{a^2}} \\ { – 2} \end{array}} \right)\)
correct working A1
eg\(\;\;\;y = \frac{2}{a} + \frac{2}{a},{\text{ }}\left( {\begin{array}{*{20}{c}} a \\ {\frac{2}{a}} \end{array}} \right) – \left( {\begin{array}{*{20}{c}} a \\ { – \frac{2}{a}} \end{array}} \right)\)
finding correct expression for \(y\) A1
eg\(\;\;\;y = \frac{4}{a},{\text{ }}\left( {\begin{array}{*{20}{c}} 0 \\ {\frac{4}{a}} \end{array}} \right)\) \({\text{P}}\left( {0,{\text{ }}\frac{4}{a}} \right)\) AG N0
[6 marks]
valid approach M1
eg\(\;\;\;\)distance formula, Pythagorean Theorem, \(\overrightarrow {{\text{PQ}}} = \left( {\begin{array}{*{20}{c}} {2a} \\ { – \frac{4}{a}} \end{array}} \right)\)
correct simplification A1
eg\(\;\;\;{(2a)^2} + {\left( {\frac{4}{a}} \right)^2}\)
\(d = 4{a^2} + \frac{{16}}{{{a^2}}}\) AG N0
[2 marks]
recognizing need to find derivative (M1)
eg\(\;\;\;d’,{\text{ }}d'(a)\)
correct derivative A2
eg\(\;\;\;8a – \frac{{32}}{{{a^3}}},{\text{ }}8x – \frac{{32}}{{{x^3}}}\)
setting their derivative equal to \(0\) (M1)
eg\(\;\;\;8a – \frac{{32}}{{{a^3}}} = 0\)
correct working (A1)
eg\(\;\;\;8a = \frac{{32}}{{{a^3}}},{\text{ }}8{a^4} – 32 = 0\)
working towards solution (A1)
eg\(\;\;\;{a^4} = 4,{\text{ }}{a^2} = 2,{\text{ }}a = \pm \sqrt 2 \)
\(a = \sqrt[4]{4}\;\;\;(a = \sqrt 2 )\;\;\;({\text{do not accept }} \pm \sqrt 2 )\) A1 N3
[7 marks]
Total [17 marks]
