Question
A function f is defined by f ( x ) = \(x\sqrt{1-x^{2}} where -1\leq x\leq 1.\)
The graph of y = f (x) is shown below.
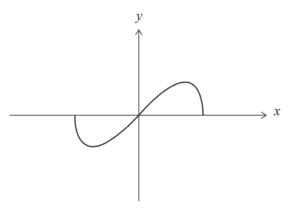
(a) Show that f is an odd function.
The range of f is a ≤ y ≤ b , where a, b ∈ R.
(b) Find the value of a and the value of b.
Answer/Explanation
Ans:
(a) attempts to replace x with –x
\(f(-x) = -x\sqrt{1-(-x)^{2}}\)
\(= -x\sqrt{1-(-x)^{2}} \left ( =-f(x) \right )\)
Note: Award M1A1 for an attempt to calculate both f (-x ) and – f (-x) independently, showing that they are equal.
Note: Award M1A0 for a graphical approach including evidence that either the graph is invariant after rotation by 180° about the origin or the graph is invariant after a reflection in the y-axis and then in the x-axis (or vice versa).
so f is an odd function
(b) attempts both product rule and chain rule differentiation to find f¢(x)
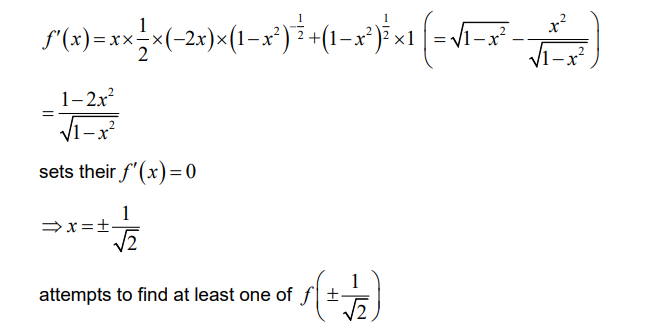
Note: Award M1 for an attempt to evaluate f(x) at least at one of their f¢(x) = 0 roots.
\(a = -\frac{1}{2} and b = \frac{1}{2}\)
Note: Award A1 for \(-\frac{1}{2}\leq y\leq \frac{1}{2}.\)
Question
Prove by contradiction that the equation 2x3 + 6x + 1 = 0 has no integer roots.
Answer/Explanation
Ans:
METHOD 1 (rearranging the equation)
assume there exists some α∈ Z such that 2α3 + 6α + 1 = 0
Note: Award M1 for equivalent statements such as ‘assume that α is an integer root of \(2\alpha ^{3} + 6\alpha +1 = 0′.\) Condone the use of x throughout the proof. Award Award M1 for an assumption involving for an assumption involving \(\alpha ^{3} + 3\alpha +\frac{1}{2} = 0.\)
Note: Award M0 for statements such as “let’s consider the equation has integer roots…” ,“let α ∈ Z be a root of 2α3 + 6α + 1 = 0 ….”
Note: Subsequent marks after this M1 are independent of this M1 and can be awarded.
attempts to rearrange their equation into a suitable form
EITHER



