Question
[Maximum mark: 6]
Cabin boy Jim is at the top of a cliff on Tortuga Island, standing $100 \mathrm{~m}$ above the sea level, and observes two ships in the Caribbean sea.
The Black Pearl $(\mathrm{P})$ is at an angle of depression of $25^{\circ}$ and the Hispaniola $(\mathrm{H})$ is at an angle of depression of $50^{\circ}$.
The following three dimensional diagram shows the foot of the cliff at $\mathrm{O}$, Jim at $\mathrm{J}$, two ships at $\mathrm{P}$ and $\mathrm{H}$, and the angle $\mathrm{POH}=75^{\circ}$.
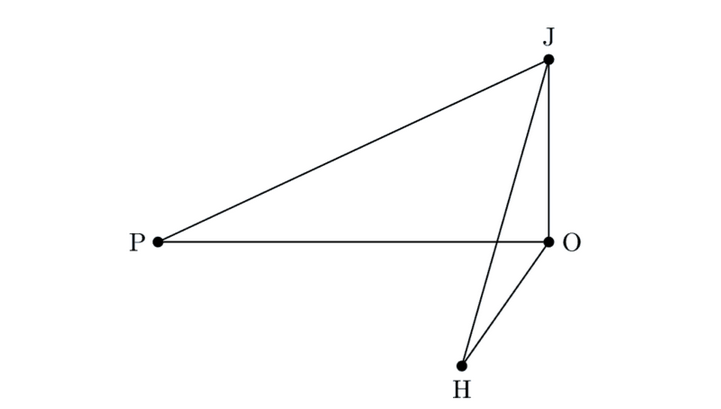
Find the distance between the two ships, giving your answer correct to 3 significant figures.
Answer/Explanation
Using the right triangle $\mathrm{JOP}$, we have
$
\begin{aligned}
\tan (\mathrm{O\hat{P}} J) & =\frac{\mathrm{JO}}{\mathrm{OP}} \\
\tan 25^{\circ} & =\frac{100}{\mathrm{OP}} \\
\mathrm{OP} & =\frac{100}{\tan 25^{\circ}} \\
\mathrm{OP} & \approx 214.45 \mathrm{~m}
\end{aligned}
$
Using the right triangle $\mathrm{JOH}$, we have
$
\begin{aligned}
\tan (\mathrm{O\hat{H}} J) & =\frac{\mathrm{JO}}{\mathrm{OH}} \\
\tan 50^{\circ} & =\frac{100}{\mathrm{OH}} \\
\mathrm{OH} & =\frac{100}{\tan 50^{\circ}} \\
\mathrm{OH} & \approx 83.910 \mathrm{~m}
\end{aligned}
$
Hence, using the cosine rule, we get
$
\begin{aligned}
\mathrm{PH}^2 & =\mathrm{OP}^2+\mathrm{OH}^2-2(\mathrm{OP})(\mathrm{OH}) \cos (\mathrm{PO} H) \\
\mathrm{PH} & =\sqrt{(214.45)^2+(83.910)^2-2(214.45)(83.910) \cos 75^{\circ}} \\
\mathrm{PH} & \approx 209 \mathrm{~m}
\end{aligned}
$
Question
[Maximum mark: 6]
The following table shows the number of skateboards $y$ that are sold $x$ days after the shop opened.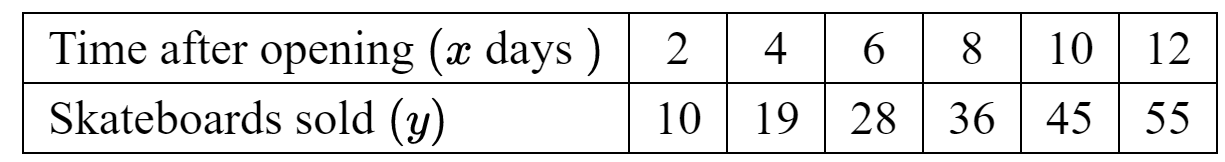
This data can be modelled by the regression line with equation $y=a x+b$.
(a) (i) Write down the value of $a$ and the value of $b$.
(ii) Explain what the gradient $a$ represents. [4]
(b) Use the model to estimate the number of skateboards sold in 5 days after the shop opened. Round your answer to the nearest integer. [2]
Answer/Explanation
(a) (i) $a \approx 4.44$ and $b \approx 1.07$ [by using G.D.C.]
(ii) 4.44; each day after the shop opened the number of skateboards sold increases by $4.44$
(b) Evaluating $y=4.44 x+1.07$ for $x=5$, we get
$
\begin{aligned}
y & =4.44(5)+1.07 \\
& =23.27 \\
& \approx 23 \text { skateboards }
\end{aligned}
$
