Question
The following diagram shows a circle with centre O and radius 5 metres.
Points A and B lie on the circle and \(A\hat{O}B\) 1.9 = radians.
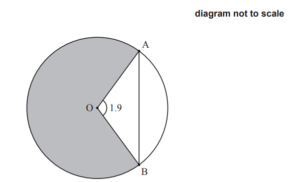
(a) Find the length of the chord [AB].
(b) Find the area of the shaded sector.
Answer/Explanation
Ans:
(a) EITHER
uses the cosine rule
AB2 = 52 + 52 -2 × 5 × 5 × cos1.9
OR
uses right-angled trigonometry
\(\frac{\frac{AB}{2}}{5}= sin 0.95\)
OR
uses the sine rule
\(\alpha = \frac{1}{2}\left ( \pi -1.9 \right )\left ( =0.6207… \right )\)
\(\frac{AB}{sin 1.9}=\frac{5}{sin 0.6207…}\)
THEN
AB = 8.13415…
AB = 8.13 (m)
(b) let the shaded area be A
METHOD 1
attempt at finding reflex angle
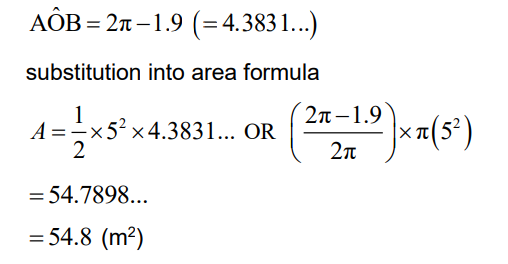
METHOD 2
let the area of the circle be AC and the area of the unshaded sector be AU
A = AC – AU
\(A = \pi \times 5^{2}-\frac{1}{2}\times 5^{2}\times 1.9(78.5398…-23.75)\)
= 54.7898…
= 54.8 (m2)
Question
A farmer is placing posts at points A, B, and C in the ground to mark the boundaries of a triangular piece of land on his property.
From point A, he walks due west 230 metres to point B.
From point B, he walks 175 metres on a bearing of 063° to reach point C.
This is shown in the following diagram.
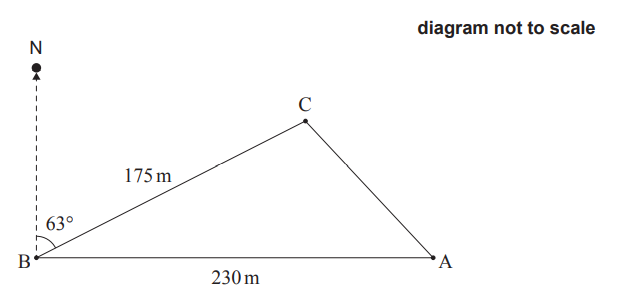
(a) Find the distance from point A to point C.
(b) Find the area of this piece of land.
(c) Find CÂB.
The farmer wants to divide the piece of land into two sections. He will put a post at point D, which is between A and C. He wants the boundary BD to divide the piece of land such that the sections have equal area. This is shown in the following diagram.
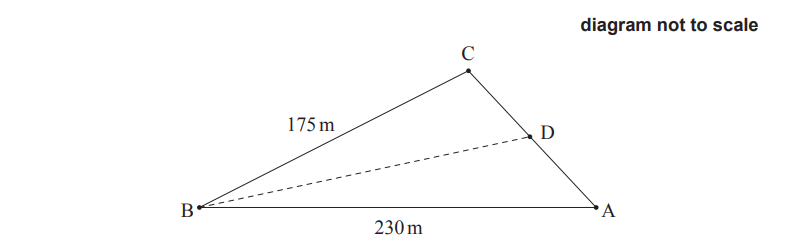
(d) Find the distance from point B to point D.
Answer/Explanation
Ans:
(a) \(A\hat{B}C = 27^{0}\)
attempt to substitute into cosine rule
1752 + 2302 – 2(175) (230) cos 270
108.62308….
AC = 109 (m)
(b) correct substitution into area formula
\(\frac{1}{2}\times 175 \times 230\times sin27^{0}\)
9136.55…
area = 9140 (m2)
(c) attempt to substitute into sine rule or cosine rule
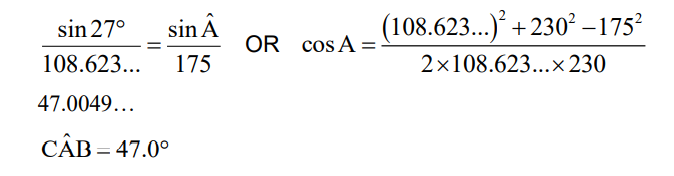
(d) METHOD 1
recognizing that for areas to be equal, AD=DC
\(AD = \frac{1}{2}AC = 54.3115…\)
attempt to substitute into cosine rule to find BD
correct substitution into cosine rule
BD2 = 2302 + 54.31152 – 2(230) (54.3115) cos 47.00490
BD = 197.009….
BD = 197 (m)
METHOD 2
correct expressions for areas of triangle BDA and triangle BCD using BD

