Question
The function $f(x) = x^3 – 3x^2 + 2x + 4$ has a stationary point at $x = 1$. Find the nature of this stationary point.
▶️Answer/Explanation
Sol:
To determine the nature of the stationary point, we need to find the second derivative of the function at that point. The first derivative of $f(x)$ is $f'(x) = 3x^2 – 6x + 2$, and the second derivative is $f”(x) = 6x – 6$. When $x = 1$, $f”(1) = 0$, which means the nature of the stationary point cannot be determined using the second derivative test. However, we can use the first derivative test by examining the sign of $f'(x)$ near $x = 1$. We find that $f'(x) < 0$ for $x < 1$ and $f'(x) > 0$ for $x > 1$, which means that $x = 1$ is a local minimum of $f(x)$. Therefore, the nature of the stationary point is a local minimum.
Question
Find the total area of the regions contained by $y=f(x)$ and the $x$-axis for $f(x)=x^3+2 x^2-3 x$.
▶️Answer/Explanation
Sol:
$$
\begin{aligned}
f(x) & =x^3+2 x^2-3 x \\
& =x\left(x^2+2 x-3\right) \\
& =x(x-1)(x+3)
\end{aligned}
$$
$\therefore y=f(x)$ cuts the $x$-axis at 0,1 , and -3 .
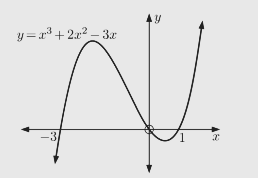
$$
\begin{aligned}
&\rm {Total ~ area}=\int_{-3}^0\left(x^3+2 x^2-3 x\right) d x-\int_0^1\left(x^3+2 x^2-3 x\right) d x \\
& =\left[\frac{x^4}{4}+\frac{2 x^3}{3}-\frac{3 x^2}{2}\right]_{-3}^0-\left[\frac{x^4}{4}+\frac{2 x^3}{3}-\frac{3 x^2}{2}\right]_0^1 \\
& =\left(0-\left(-11 \frac{1}{4}\right)\right)-\left(-\frac{7}{12}-0\right) \\
& =11 \frac{5}{6} \text { units }^2
\end{aligned}
$$
