Question
A sector of a circle, centre O and radius 4.5m, is shown in the following diagram.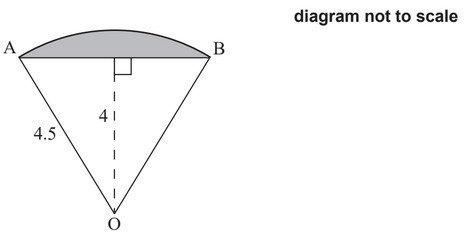
(a) (i) Find the angle AÔB.
(ii) Find the area of the shaded segment.
A square field with side 8m has a goat tied to a post in the centre by a rope such that the
goat can reach all parts of the field up to 4.5m from the post.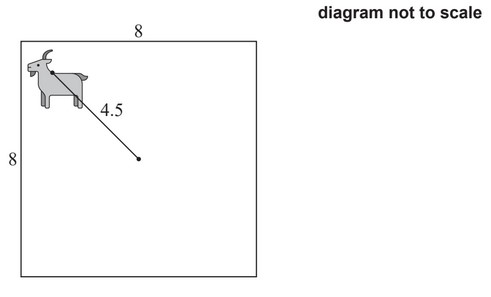
(b) Find the area of the field that can be reached by the goat.
Let V be the volume of grass eaten by the goat, in cubic metres, and t be the length of time,
in hours, that the goat has been in the field.
The goat eats grass at the rate of \(\frac{dV}{dt}=0.3te^{-t}\).
(c) Find the value of t at which the goat is eating grass at the greatest rate.
The goat is tied in the field for 8 hours.
(d) Find the total volume of grass eaten by the goat during this time.
Answer/Explanation
Ans:


Question
The graph alongside shows how a cyclist accelerates away from an intersection.
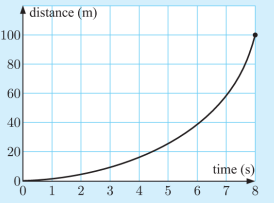
a. Estimate the instantaneous speed of the cyclist after:
i) 4 seconds
ii) 6 seconds.
b. Describe what happens to the cyclist’s speed over time.
▶️Answer/Explanation
(a)
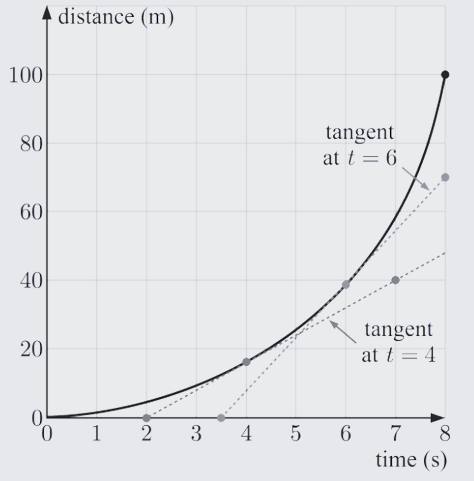
i)
The tangent at $t=4$ passes through $(2,0)$ and $(7,40)$.
$\therefore$ the instantaneous speed at $t=4$
$$
\begin{aligned}
& =\frac{(40-0) \mathrm{m}}{(7-2) \mathrm{s}} \\
& =\frac{40}{5} \mathrm{~ms}^{-1} \\
& =8 \mathrm{~ms}^{-1}
\end{aligned}
$$
ii)
The tangent at $t=6$ passes through $(3.5,0)$ and $(8,70)$.
$\therefore$ the instantaneous speed at $t=6$
$$
\begin{aligned}
& =\frac{(70-0) \mathrm{m}}{(8-3.5) \mathrm{s}} \\
& =\frac{70}{4.5} \mathrm{~m} \mathrm{~s}^{-1} \\
& \approx 15.6 \mathrm{~m} \mathrm{~s}^{-1}
\end{aligned}
$$
b) As time increases, the tangent to the curve gets steeper and steeper. The gradient of the tangent is increasing, so the speed of the cyclist is increasing.
