Question
A particle P moves along the x-axis. The velocity of P is v m s–1 at time t seconds, where
v = −2t2 + 16t − 24 for t ≥ 0.
a. Find the times when P is at instantaneous rest. [2]
b. Find the magnitude of the particle’s acceleration at 6 seconds. [4]
c. Find the greatest speed of P in the interval 0 ≤ t ≤ 6. [2]
d. The particle starts from the origin O. Find an expression for the displacement of P from O at time t seconds. [4]
e. Find the total distance travelled by P in the interval 0 ≤ t ≤ 4. . [3]
Answer/Explanation
(a) solving v = 0 t= 2, t= 6
(b)use of power rule \(\frac{dv}{dt}=-4t+16 (t=6)\Rightarrow a=-8magnitude = 8 ms^{-2}\)
(c) using a sketch graph of \(v=24ms^{-1}\)
(d) \(x=\int vdt\) attempt at integration of
\(v -\frac{2t^{3}}{3}+8t^{2}-24t+c\)
attempt to find c (use of t x = 0 = x= 0)
\(c = 0\) \(x=-\frac{2t^{3}}{3}+8t^{2}-24t)\)
(e) \(\int_{0}^{4}|v|dt = 32 m\)
Question
Consider the following system of coupled differential equations.
\(\frac{dx}{dt}\)= −4x
\(\frac{dx}{dt}\)= 3x − 2y
a. Find the eigenvalues and corresponding eigenvectors of the matrix 
[6]
b. Hence, write down the general solution of the system. [2]
c. Determine, with justification, whether the equilibrium point (0, 0) is stable or unstable. [2]
d. Find the value of \(\frac{dy}{dx}\)
(i) at (4 , 0).
(ii) at (−4, 0). [3]
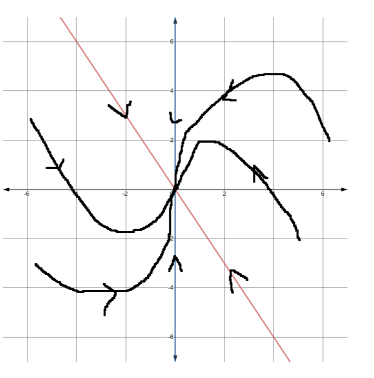
e. Sketch a phase portrait for the general solution to the system of coupled differential equations for −6 ≤ x ≤ 6, −6 ≤ y ≤ 6. [4]
Answer/Explanation
(a)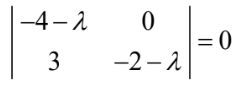 
\( (-4-\lambda )(-2-\lambda )=0\)
\(\lambda =-4\) OR \(\lambda =-2 \)
\(\lambda =-4\)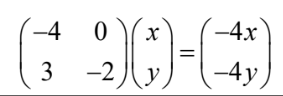 
\(3x-2y=-4y\)
\(3x=-2y\)
possible eigenvector is \((_{3}^{-2})(or any real multiple) \lambda =-2\)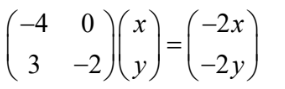 
\(x = 0, y = 1\) possible eigenvector is \((_{1}^{0}) (or any real multiple)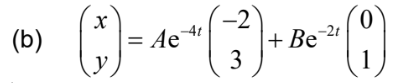 
(c) two (distinct) real negative eigenvalues (or equivalent (eg both \(e^{-4t}\rightarrow 0,e^{-2t}\rightarrow 0 as t\rightarrow \)∞ ⇒ stable equilibrium point
(d)\(\frac{dy}{dx}=\frac{3x-2y}{-4x}(i)(4,0)\Rightarrow \frac{dy}{dx}=-\frac{3}{4}(ii)(-4,0)\Rightarrow \frac{dy}{dx}=-\frac{3}{4}\)
(e) 