Question
A farmer owns a field in the shape of a triangle ABC such that AB = 650 m, AC = 1005 m
and BC = 1225 m
diagram not to scale
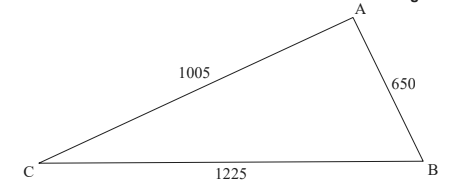
a. Find the size of AĈB. [3]
The local town is planning to build a highway that will intersect the borders of the field at points D and E, where DC = 210 m and CÊD = 100° , as shown in the diagram below.
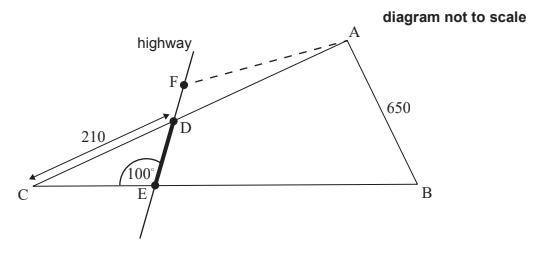
b. Find DE. [3]
The town wishes to build a carpark here. They ask the farmer to exchange the part of the field represented by triangle DCE. In return the farmer will get a triangle of equal area ADF, where F lies on the same line as D and E, as shown in the diagram above.
c. Find the area of triangle DCE. [5]
d. Estimate DF. You may assume the highway has a width of zero. [4]
Answer/Explanation
(a) cosine rule ACB = \(cos^{-1}(\frac{1005^{2}+1225^{2}-650^{2}}{2\times 1005\times 1225})\)
\(= 32.0 ((31.9980…)\) OR \(0.558 (0.558471…)\)
(b) sine rule \(\frac{DE}{sin31.9980..}= \frac{210}{sin100}\)
\(DE = 113 m (112.9937…)\)
(c) \(180-(100 +their part (a))=48.0019\) OR
\(0.837791…\(\frac{1}{2}\times 112.9937…\times 210\times sin48.002\)
\(8820m^{2}\rightarrow (8817.18 )\)
(d) \(1005 − 210 \) OR \(795\)
equating answer to part (c) to area of a triangle formula
\(8817.18..=\frac{1}{2}\times DF\times (1005-210)\times sin48.002..\)
\((DF=)29.8m(29.8473….)\)
Question
A particle moves in a straight line with position relative to $O$ given by $s(t)=t^3-3 t+1 \mathrm{~cm}$, where $t$ is the time in seconds, $t \geqslant 0$.
a. Find expressions for the particle’s velocity and acceleration, and draw sign diagrams for each of them.
b. Find the initial conditions and hence describe the motion of the particle at this instant.
c. Describe the motion of the particle at $t=2$ seconds.
d. Find the position of the particle when it changes direction.
e. Draw a motion diagram for the particle.
f. For what time interval is the particle’s speed increasing?
▶️Answer/Explanation
Solution:
a)
$$
\begin{aligned}
s(t) & =t^3-3 t+1 \mathrm{~cm} \\
\therefore \quad v(t) & =3 t^2-3 \quad\left\{v(t)=s^{\prime}(t)\right\} \\
& =3\left(t^2-1\right) \\
& =3(t+1)(t-1) \mathrm{cm}~ \mathrm{s}^{-1}
\end{aligned}
$$
which has sign diagram:
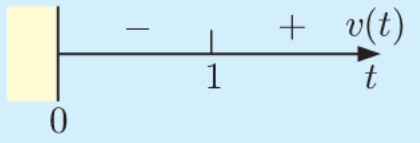
and $a(t)=6 t \mathrm{~cm} \mathrm{~s}^{-2} \quad\left\{a(t)=v^{\prime}(t)\right\}$
which has sign diagram:
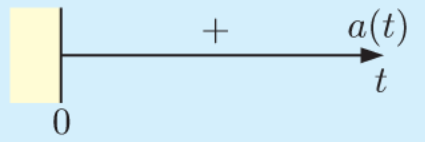
b)
When $t=0, s(0)=1 \mathrm{~cm}$
$$
\begin{aligned}
& v(0)=-3 \mathrm{~cm} \mathrm{~s}^{-1} \\
& a(0)=0 \mathrm{~cm} \mathrm{~s}^{-2}
\end{aligned}
$$
$\therefore$ the particle is $1 \mathrm{~cm}$ to the right of $\mathrm{O}$, moving to the left at a speed of $3 \mathrm{~cm} \mathrm{~s}^{-1}$.
c)
When $t=2, \quad s(2)=8-6+1=3 \mathrm{~cm}$
$$
\begin{aligned}
& v(2)=12-3=9 \mathrm{~cm} \mathrm{~s}^{-1} \\
& a(2)=12 \mathrm{~cm} \mathrm{~s}^{-2}
\end{aligned}
$$
$\therefore$ the particle is $3 \mathrm{~cm}$ to the right of $\mathrm{O}$, moving to the right at a speed of $9 \mathrm{~cm} \mathrm{~s}^{-1}$. Since $a$ and $v$ have the same sign, the speed of the particle is increasing.
d)
Since $v(t)$ changes sign when $t=1$, a change of direction occurs at this instant. $s(1)=1-3+1=-1, \quad$ so the particle changes direction when it is $1 \mathrm{~cm}$ to the left of $\mathrm{O}$.
e)
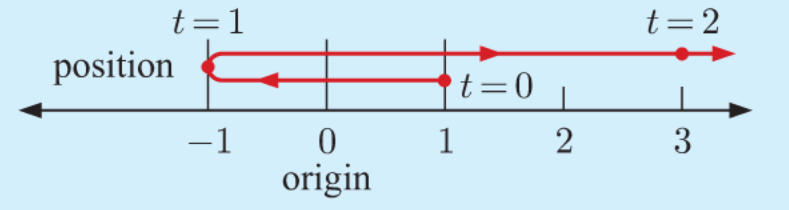
f)
f Speed is increasing when $v(t)$ and $a(t)$ have the same sign. This is for $t \geqslant 1$.
