Question
A psychologist records the number of digits ( d ) of π that a sample of IB Mathematics higher
level candidates could recall.
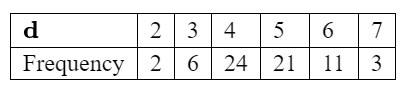
(a) Find an unbiased estimate of the population mean of d.
(b) Find an unbiased estimate of the p The psychologist has read that in the general population people can remember an average of 4.4 digits of π. The psychologist wants to perform a statistical test to see if IB Mathematics higher level candidates can remember more digits than the general population.opulation variance of d.
(c) \(H_0 : \mu = 4.4\) is the null hypothesis for this test.
(i) State the alternative hypothesis.
(ii) Given that all assumptions for this test are satisfied, carry out an appropriate hypothesis test. State and justify your conclusion. Use a 5% significance level.
Answer/Explanation
Ans:
(a) \(\overrighthat{x} = 4.63 (4.62686…)\)
(b) \(S_{n-1} = 1.098702\)
\(S_{n-1}=1.21 (1.207146…)\)
(c) (i) \(H_1 : \mu > 4.4\)
(ii) METHOD 1
using a z-test
p = 0.0454992…
p<0.05
reject null hypothesis
(therefore there is significant evidence that the IB HL math students know more digits
of π than the population in general)
METHOD 2
using a t-test
p = 0.0478584…
p<0.05
(therefore there is significant evidence that the IB HL math students know more digits
of π than the population in general)
Question
A function f is of the form \(f(t)=pe^{q cos (rt)},p, q, r \epsilon \mathbb{R}^+\). Part of the graph of f is shown.
The points A and B have coordinates A(0 , 6.5) and B(5.2 , 0.2), and lie on f .
The point A is a local maximum and the point B is a local minimum.
Find the value of p, of q and of r.
Answer/Explanation
Ans:

