Question
[Maximum mark: 6]
A triangle with vertices $\mathrm{A}(6,6), \mathrm{B}(3,1)$ and $\mathrm{C}(1,3)$ is transformed by $\mathbf{x}^{\prime}=\mathbf{A} \mathbf{x}+\mathbf{b}$ where $\mathbf{A}=\left(\begin{array}{ll}-1 & 2 \\ -2 & 1\end{array}\right)$ and $\mathbf{b}=\left(\begin{array}{c}-6 \\ 3\end{array}\right)$.
(a) On the following grid, draw the image of the triangle ABC. [3]
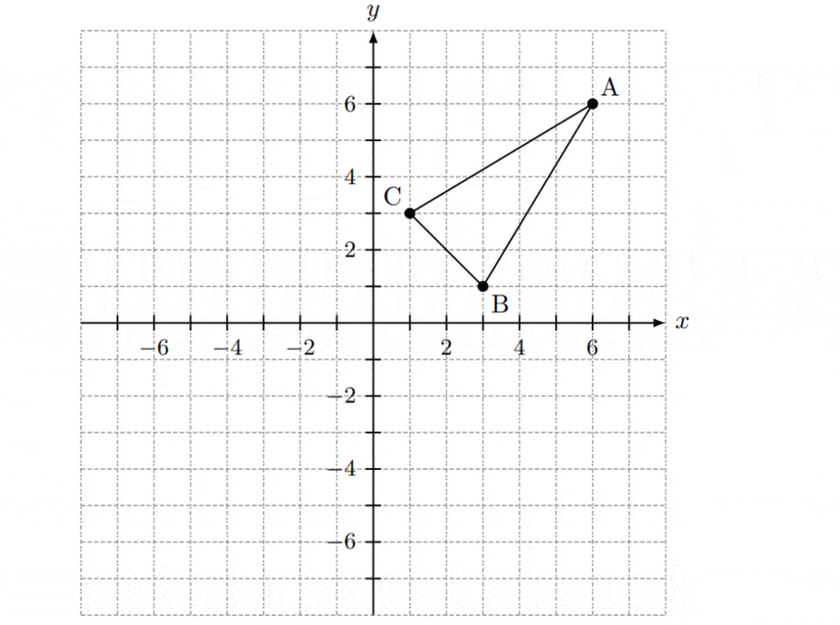
(b) Given the area of the triangle $\mathrm{ABC}$ is $16 \mathrm{units}^2$, find the area of its image. [3]
Answer/Explanation
(a) Let $\mathrm{A}^{\prime}, \mathrm{B}^{\prime}, \mathrm{C}^{\prime}$ be the image points of $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$.
Using the position vector of $A$, we get
$
\begin{aligned}
\overrightarrow{\mathrm{OA}^{\prime}} & =\left(\begin{array}{ll}
-1 & 2 \\
-2 & 1
\end{array}\right) \overrightarrow{\mathrm{OA}}+\left(\begin{array}{c}
-6 \\
3
\end{array}\right) \\
& =\left(\begin{array}{ll}
-1 & 2 \\
-2 & 1
\end{array}\right)\left(\begin{array}{l}
6 \\
6
\end{array}\right)+\left(\begin{array}{c}
-6 \\
3
\end{array}\right) \\
& =\left(\begin{array}{c}
0 \\
-3
\end{array}\right)
\end{aligned}
$
Hence the coordinates of $\mathrm{A}^{\prime}$ are $(0,-3)$.
Using the position vector of $\mathrm{B}$, we obtain
$
\begin{aligned}
\overrightarrow{\mathrm{OB}^{\prime}} & =\left(\begin{array}{ll}
-1 & 2 \\
-2 & 1
\end{array}\right) \overrightarrow{\mathrm{OB}}+\left(\begin{array}{c}
-6 \\
3
\end{array}\right) \\
& =\left(\begin{array}{ll}
-1 & 2 \\
-2 & 1
\end{array}\right)\left(\begin{array}{l}
3 \\
1
\end{array}\right)+\left(\begin{array}{c}
-6 \\
3
\end{array}\right) \\
& =\left(\begin{array}{l}
-7 \\
-2
\end{array}\right)
\end{aligned}
$
Hence the coordinates of $\mathrm{B}^{\prime}$ are $(-7,-2)$.
Using the position vector of $\mathrm{C}$, we find
$
\begin{aligned}
\overrightarrow{\mathrm{OC}^{\prime}} & =\left(\begin{array}{ll}
-1 & 2 \\
-2 & 1
\end{array}\right) \overrightarrow{\mathrm{OC}}+\left(\begin{array}{c}
-6 \\
3
\end{array}\right) \\
& =\left(\begin{array}{ll}
-1 & 2 \\
-2 & 1
\end{array}\right)\left(\begin{array}{l}
1 \\
3
\end{array}\right)+\left(\begin{array}{c}
-6 \\
3
\end{array}\right) \\
& =\left(\begin{array}{c}
-1 \\
4
\end{array}\right)
\end{aligned}
$
Hence the coordinates of $\mathrm{C}^{\prime}$ are $(-1,4)$.
Question
[Maximum mark: 6]
The Voronoi diagram below shows the fitness studios A, B and C, located in a particular district.
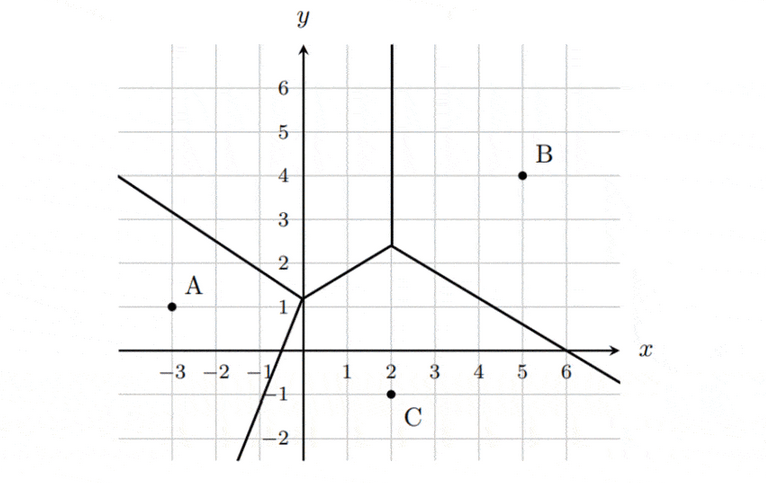
(a) On the diagram, shade the cell with the missing fitness studio. [2]
(b) Determine the coordinates of the missing fitness studio, D. [2]
(c) Jennifer lives an equal distance from fitness studios A and D. Find the shortest possible distance Jennifer’s house could be from fitness studios A and D. [2]
Answer/Explanation
(a) 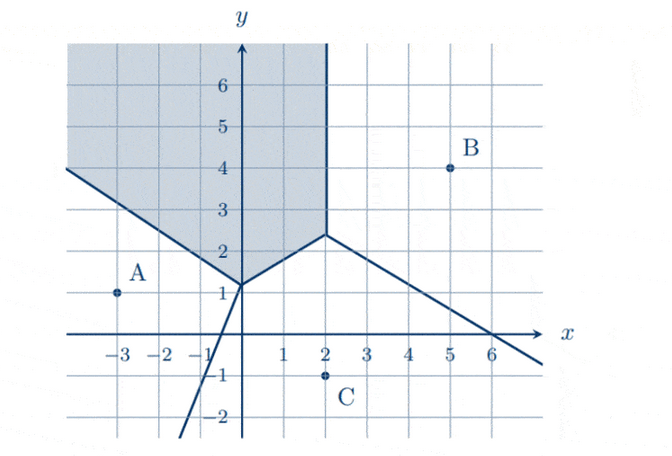
(b) The missing studio $\mathrm{D}$ will be the same distance from the line $x=2$ as studio $\mathrm{B}$, since the perpendicular bisector $\mathrm{BD}$ is vertical. The distance between $x=2$ and $\mathrm{B}$ is $3 \mathrm{~km}$. Hence the missing fitness studio D is located at $\mathrm{D}(-1,4)$
(c) Jennifer’s house is at the midpoint of [AD]. Hence,
$
\begin{aligned}
d & =\frac{1}{2}[\mathrm{AD}] \\
& =\frac{1}{2} \sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2} \\
& =\frac{1}{2} \sqrt{(-3-(-1))^2+(1-4)^2} \\
& =\frac{1}{2} \sqrt{4+9} \\
& \approx 1.80 \mathrm{~km}
\end{aligned}
$
