Question
Use the trapezoidal rule with 6 subintervals to estimate the area between $f(x)=\sqrt{6-x^2}$ and the $x$-axis from $x=1$ to $x=2$.
▶️Answer/Explanation
Sol:
$\begin{aligned} & n=6, a=1, b=2, \quad f(x)=\sqrt{6-x^2} \\ & h=\frac{b-a}{n}=\frac{1}{6} \\ & x_i=1+\frac{1}{6} i\end{aligned}$
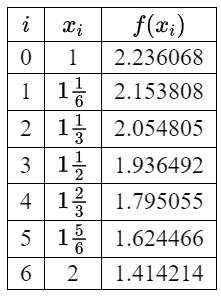
Using the trapezoidal rule, the area
$$
\begin{aligned}
& \approx \frac{h}{2}\left(f\left(x_0\right)+2 f\left(x_1\right)+2 f\left(x_2\right)+\ldots .+2 f\left(x_5\right)+f\left(x_6\right)\right) \\
& \approx 1.8983 \text { units }^2
\end{aligned}
$$
Question
Charles has set a goal for his New Year’s resolution to complete 100 pushups without a break. He begins with a training routine where he starts with 20 pushups on the first day and adds 5 more pushups each day.
(a) What is the total number of pushups Charles completes on the 4th training day and on the nth training day?
(b) On which day of training does Charles first complete 100 pushups in one go?
(c) How many pushups does Charles complete in the first 10 days of training?
Additionally, Charles is preparing for an Iron Man event in 12 weeks and wants to improve his long-distance swimming. He starts by swimming 10,000 meters in the first week and plans to increase this distance by 10% each week until the event.
(d) What distance will Charles swim in the 6th week of training?
Answer/Explanation
(a) We can represent the number of pushups Charles completes on the $n$th day as an arithmetic sequence with the first term $u_1=20$ and the common difference $d=5$. Using the $n$th term formula $u_n=u_1+(n-1) d$, we can find the number of pushups Charles completes on the 4th training day by substituting $n=4$ into the formula:
$$
u_4 = u_1 + (4-1)d = 20 + (4-1)(5) = 35.
$$
To find the number of pushups Charles completes on the $n$th training day, we can use the same formula:
$$
u_n = u_1 + (n-1)d = 20 + (n-1)(5) = 5n + 15.
$$
(b) To find the day of training when Charles first completes 100 pushups in one go, we need to solve the equation $u_k = 100$ for $k$. Substituting $u_k = 20 + (k-1)(5)$ and solving for $k$, we get:
$$
20 + (k-1)(5) = 100 \quad \Rightarrow \quad k = 17.
$$
Therefore, Charles completes 100 pushups for the first time on the 17th day of training.
(c) The total number of pushups Charles completes in the first 10 days of training can be found using the sum of $n$ terms formula for an arithmetic sequence, which is $S_n = \frac{n}{2}(2u_1 + (n-1)d)$. Substituting $n=10$, $u_1=20$, and $d=5$, we get:
$$
S_{10} = \frac{10}{2}(2 \times 20 + (10-1) \times 5) = 425.
$$
Therefore, Charles completes a total of 425 pushups in the first 10 days of training.
(d) The distance Charles swims in the $n$th week of training can be represented as a geometric sequence with the first term $v_1=10000$ and the common ratio $r=1.1$. Using the $n$th term formula $v_n = v_1 r^{n-1}$, we can find the distance Charles swims in the 6th week of training by substituting $n=6$:
$$
v_6 = v_1 r^{6-1} = 10000 (1.1)^{5} \approx 16100\mathrm{~m}.
$$
Therefore, Charles swims approximately 16100 meters in the 6th week of training.
