Question
A group of 130 applicants applied for admission into either the Arts programme or the Sciences programme at a iuniversity. The outcomes of their applications are shown in the following table.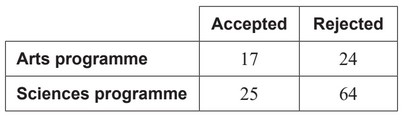
(a) Find the probability that a randomly chosen applicant from this group was accepted by
the university.
An applicant is chosen at random from this group. It is found that they were accepted into the
programme of their choice.
(b) Find the probability that the applicant applied for the Arts programme.
Two different applicants are chosen at random from the original group.
(c) Find the probability that both applicants applied to the Arts programme.
Answer/Explanation
Ans:
(a) \((\frac{17+25}{130}=)\) \(\frac{42}{130} (\frac{21}{65},0.323076…)\)
(b) \((\frac{17}{17+25}=) \frac{17}{42} (0.404761…)\)
(c) \(\frac{41}{130} \times \frac{40}{129}\)
\(=\frac{1640}{16770} \approx 0.0978 (0.0977936…, \frac{164}{1677})\)
Question
A vertical pole stands on horizontal ground. The bottom of the pole is taken as the origin, O,
of a coordinate system in which the top, F, of the pole has coordinates (0, 0, 5.8). All units
are in metres.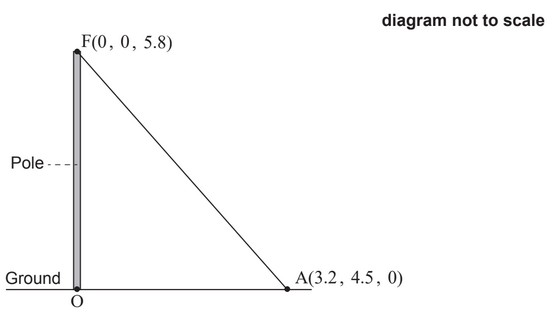
The pole is held in place by ropes attached at F.
One of the ropes is attached to the ground at a point A with coordinates (3.2, 4.5, 0).
The rope forms a straight line from A to F.
(a) Find the length of the rope connecting A to F.
(b) Find \(F \widehat{A} O\), the angle the rope makes with the ground.
Answer/Explanation
Ans:
(a) \(\sqrt{3.2^2 + 4.5^2 +5.8^2}\)
=8.01 (8.00812…) m
(b) \(F\widehat{A} O = sin^{-1} (\frac{5.8}{8.00812…})\) OR \(cos^{-1}(\frac{5.52177…}{8.00812…})\) OR \(tan^{-1}(\frac{5.8}{5.52177…})\)
\(46.4^o (46.4077…^o)\)
