Question
A sector of a circle, centre O and radius 4.5m, is shown in the following diagram.
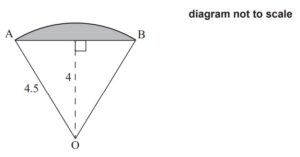
(a) (i) Find the angle AÔB.
(ii) Find the area of the shaded segment. [8]
A square field with side 8m has a goat tied to a post in the centre by a rope such that the
goat can reach all parts of the field up to 4.5m from the post.
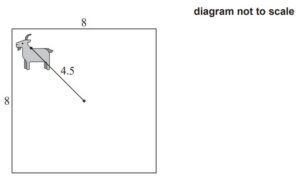
(b) (i) Find the area of a circle with radius 4.5m.
(ii) Find the area of the field that can be reached by the goat. [5]
Let V be the volume of grass eaten by the goat, in cubic metres, and t be the length of time,
in hours, that the goat has been in the field.
The goat eats grass at the rate of \(\frac{dV}{dt}=0.3te^{-t}\).
(c) Find the value of t at which the goat is eating grass at the greatest rate. [2]
Answer/Explanation
Ans
4. (a) (i) \(\left ( \frac{1}{2}A\hat{O}B= \right )\arccos \left ( \frac{4}{4.5} \right )=27.266…\) (M1)(A1)
AOB 54.532… ≈ 54.5 o = ( 0.951764…≈ 0.952 radians) A1
Note: Other methods may be seen; award (M1)(A1) for use of a correct trigonometric
method to find an appropriate angle and then A1 for the correct answer.
(ii) finding area of triangle
EITHER
area of triangle \(=\frac{1}{2}\times 4.5^{2}\times \sin (54.532…)\) (M1)
Note: Award M1 for correct substitution into formula.
= 8.24621…≈ 8.25 m2
OR
\(AB=2\times \sqrt{4.5^{2}-4^{2}}=4.1231…\) (M1)
\(area\ triangle=\frac{4.12131…\times 4}{2}\) (A1)
= 8.24621…≈ 8.25 m2
EITHER
\(area\ of \ sector=\frac{54.532…}{360}\times \pi \times 4.5^{2}\) (M1)
= 9.63661… ≈ 9.64 m2
OR
\(area\ of \ sector=\frac{1}{2}\times 0.9517641.. \times 4.5^{2}\) (M1)
= 9.63661… ≈ 9.64 m2 (A1)
THEN
area of segment = 9.63661… 8.24621… −
=1.39 m2 (1.39040…) A1
[8 marks]
(b) (i) 2 π× 4.5 (M1)
63.6 m2 (63.6172… m2 ) A1
(ii) METHOD 1
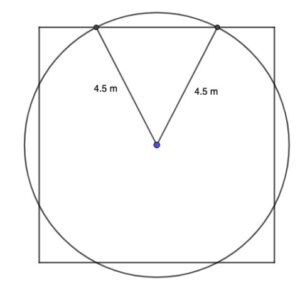
4 1.39040… × (5.56160) (A1)
subtraction of four segments from area of circle (M1)
= 58.1 m2 (58.055…) A1
METHOD 2
\(4(0.5\times 4.5^{2} \times\sin 54.532… )+4\left ( \frac{35.4679}{360}\times\pi \times 4.5^{2} \right )\) (M1)
= 32.9845… + 25.0707 (A1)
= 58.1 m2 (58.055 …) A1
[5 marks]
(c) sketch of \(\frac{dV}{dt}\) OR \(\frac{dV}{dt}=0.110363…\) OR attempt to find where \(\frac{d^{2}V}{dt^{2}}=0\) (M1)
t =1 hour A1
[2 marks]
[Total 15 marks]
Question
Find the equation of the normal to $f(x)=x^2-4 x+3$ at the point where $x=4$.
▶️Answer/Explanation
Sol:
Since $f(4)=(4)^2-4(4)+3=3$, the point of contact is $(4,3)$.
$$
\text { Now } \begin{aligned}
f(x) & =x^2-4 x+3 \\
\therefore \quad f^{\prime}(x) & =2 x-4 \\
\therefore \quad f^{\prime}(4) & =2(4)-4 \\
& =4
\end{aligned}
$$
So, the normal at $(4,3)$ has gradient $-\frac{1}{4}$.
$\therefore$ the normal has equation
$$
y=-\frac{1}{4}(x-4)+3
$$
which is
$$
y=-\frac{1}{4} x+1+3
$$
or $y=-\frac{1}{4} x+4$
The normal is perpendicular to the tangent.
