Question
[Maximum mark: 14]
Georgia is on vacation in Costa Rica. She is in a hot air balloon over a lush jungle in Muelle.
When she leans forward to see the treetops, she accidentally drops her purse. The purse falls down a distance of 4 metres during the first second, 12 metres during the next second, 20 metres during the third second and continues in this way. The distances that the purse falls during each second forms an arithmetic sequence.
(a) (i) Write down the common difference, $d$, of this arithmetic sequence.
(ii) Write down the distance the purse falls during the fourth second. [2]
(b) Calculate the distance the purse falls during the 13th second. [2]
(c) Calculate the total distance the purse falls in the first 13 seconds. [2]
Georgia drops the purse from a height of 1250 metres above the ground.
(d) Calculate the time, to the nearest second, the purse will take to reach the ground. [3]
Georgia visits a national park in Muelle. It is opened at the start of 2019 and in the first year there were 20000 visitors. The number of people who visit the national park is expected to increase by $8 \%$ each year.
(e) Calculate the number of people expected to visit the national park in 2020. [2]
(f) Calculate the total number of people expected to visit the national park by the end of 2028 . [3]
Answer/Explanation
(a) (i) We have $u_1=4$ and $u_2=12$.
Hence the common difference is
$
\begin{aligned}
d & =u_2-u_1 \\
& =12-4 \\
& =8
\end{aligned}
$
(ii) Using the $n$th term formula $u_n=u_1+(n-1) d$ with $n=4$, we get
$
\begin{aligned}
u_4 & =u_1+(4-1) d \\
& =4+(4-1)(8) \\
& =28 \mathrm{~m}
\end{aligned}
$
(b) Using the $n$th term formula $u_n=u_1+(n-1) d$ with $n=13$, we obtain
$
\begin{aligned}
u_{13} & =u_1+(13-1) d \\
& =4+(13-1)(8) \\
& =100 \mathrm{~m}
\end{aligned}
$
(c) Using the sum of $n$ terms formula $S_n=\frac{n}{2}\left(2 u_1+(n-1) d\right)$ with $n=13$, we get
$
\begin{aligned}
S_{13} & =\frac{13}{2}\left(2 u_1+(13-1) d\right) \\
& =\frac{13}{2}(2(4)+(13-1)(8)) \\
& =676 \mathrm{~m}
\end{aligned}
$
Question
[Maximum mark: 17]
A High School in Auckland, New Zealand, conducted a study on the relationship between teaching experience, in years, and teaching performance. There were 8 teachers involved in the study (labelled A to H). Teaching performances were assessed by the commission board of the school on a scale out of 100 . The data is shown in the following table.
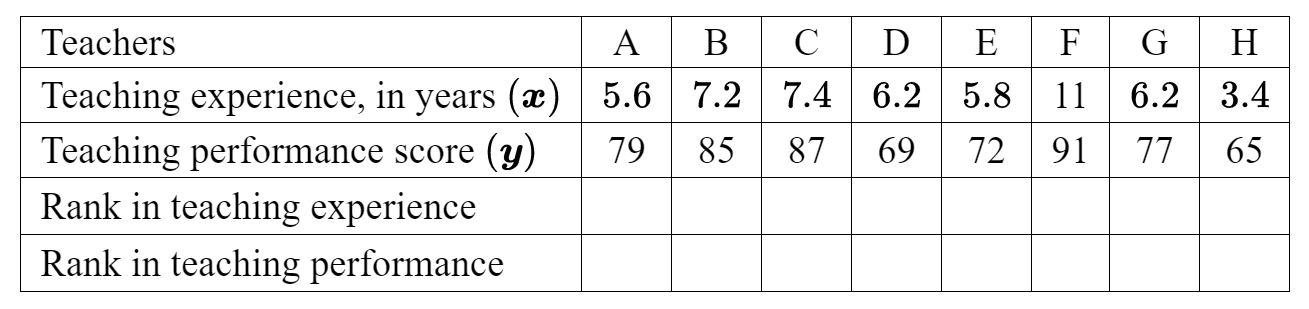
(a) (i) Find the Pearson’s product-moment correlation coefficient, $r$.
(ii) Using the value of $r$, interpret the relationship between teaching performance and teaching experience of these teachers. [4]
(b) Write down the equation of the regression line $y$ on $x$. [2]
(c) (i) Use your regression equation from part (b) to estimate the teaching performance score of a teacher who has 8 years of teaching at the school.
(ii) State whether this estimate is reliable. Justify your answer. [4]
(d) Complete the two empty rank rows in the table above. [2]
(e) (i) Find the value of the Spearman’s rank correlation coeffcient, $r_s$.
(ii) Interpret the result obtained for $r_s$. [4]
This data collected excluded the Teachers first year of teaching, as they were on probation and not fully registered yet. The commission board decided to include this period to the working experience.
(f) Explain why the value of the Spearman’s rank correlation coefficient $r_s$ does not change when this first year is included. [1]
Answer/Explanation
(a) (i) $r \approx 0.854$ $\text{[by using G.D.C.]}$
(ii) Since the correlation coefficient is positive and fairly close to 1 , there is a strong positive correlation between teaching experience and teaching performance.
(b) $y=3.62 x+54.2$ $\text{[by using G.D.C.]}$
(c) (i) Substituting $x=8$ into the equation of the regression line, we get
$
\begin{gathered}
y=3.62(8)+54.2 \\
\approx 83.1
\end{gathered}
$
(ii) The estimate is reliable as $x=8$ falls within the data range $[3.4,11]$ and the correlation is quite strong.
