Question 3 [Maximum mark: 7]
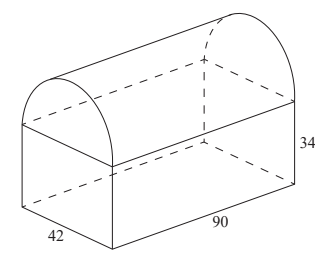
A storage container consists of a box of length 90 cm, width 42 cm and height 34 cm, and a lid in the shape of a half-cylinder, as shown in the diagram. The lid fits the top of the box exactly. The
total exterior surface of the storage container is to be painted.
Find the area to be painted. diagram not to scale
Answer/Explanation
\(2\times 90\times\times 34 =6120\) AND \(2\times 42\times 34=2856\)
\(r=21\)
\(21\Pi \times 90 =(1890\Pi , 5937.61..)\rightarrow 20100 cm2 (20079.0…)\)
use of curved surface area formula
\(\Pi \times 21^{2}\rightarrow (441\Pi ,1385.44..)\)
Question 2. [Maximum mark: 5]
An inclined railway travels along a straight track on a steep hill, as shown in the diagram.
diagram not to scale
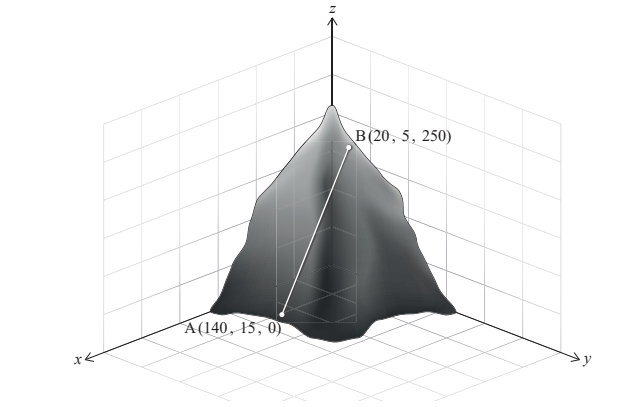
The locations of the stations on the railway can be described by coordinates in reference to x , y , and z-axes, where the x and y axes are in the horizontal plane and the z-axis is vertical.
The ground level station A has coordinates (140 , 15 , 0) and station B, located near the top of the hill, has coordinates (20 , 5 , 250). All coordinates are given in metres.
a. Find the distance between stations A and B. [2] Station M is to be built halfway between stations A and B.
b. Find the coordinates of station M. [2]
c. Write down the height of station M, in metres, above the ground. [1]
Answer/Explanation
(a) 3D distance formula \(AB= \sqrt{(140-20)^{2}+ (15-5)^{2}+250^{2}}= (\sqrt{77000})=277m (10\sqrt{770, 277.488..})\)
(b) midpoint formula \((\frac{140+20}{2},\frac{15+5}{2},\frac{0+250}{2})\) \(80, 10, 125\)
(c) 125 m
Question 3 [Maximum mark: 6]
A piece of candy is made in the shape of a solid hemisphere. The radius of the hemisphere is 6 mm.
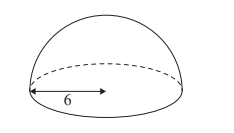
a. Calculate the total surface area of one piece of candy. [4]
The total surface of the candy is coated in chocolate. It is known that 1 gram of the chocolate covers an area of 240 mm2.
b. Calculate the weight of chocolate required to coat one piece of candy. [2]
Answer/Explanation
(a)\(\frac{1}{2}\times 4\times \pi \times 6^{2}+\pi \times 6^{2} OR \(3 \times \pi \times 6^{2}\)
\(= 339 mm^{2}(108\pi ,339.292..)\)
(b)\(\frac{339.292..}{240}=1.41g\)
\(\frac{9\pi }{20}0.45\pi ,1.41371…)\)
Question
The front view of a doghouse is made up of a square with an isosceles triangle on top.
The doghouse is 1.35 m high and 0.9m wide, and sits on a square base.
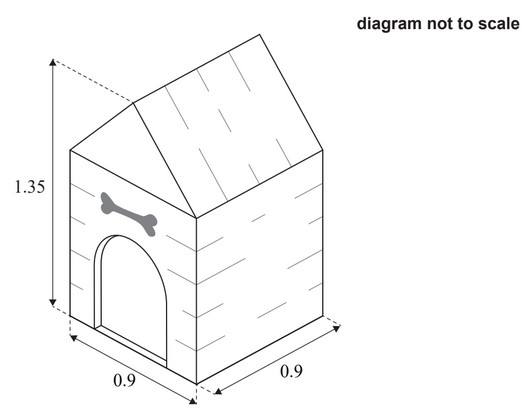
The top of the rectangular surfaces of the roof of the doghouse are to be painted
Find the area to be painted.
Answer/Explanation
Ans:
height of triangle at roof = 1.35 – 0.9 = 0.45
slant height = \(\sqrt{0.45^2 + 0.45^2}\) OR \(sin(45^o)=\frac{0.45}{slant height}\)
\(=\sqrt{0.405}(0.636396…, 0.45 \sqrt{2}\)
area of one rectangle on roof = \(\sqrt{0.405} \times 0.9 (=0.572756…)\)
area painted = \((2 \times \sqrt{0.405} \times 0.9 = 2 \times 0.572756…)\)
1.15 \(m^2\) (1.14551… \(m^2\), 0.81 \(\sqrt{2} m^2 \))
Question
P (4, 1) and Q (0, –5) are points on the coordinate plane.
Determine the
(i) coordinates of M, the midpoint of P and Q.
(ii) gradient of the line drawn through P and Q.
(iii) gradient of the line drawn through M, perpendicular to PQ.[4]
The perpendicular line drawn through M meets the y-axis at R (0, k).
Find k.[2]
Answer/Explanation
Markscheme
(i) (2, – 2) parentheses not required. (A1)
(ii) gradient of PQ \( = \left( {\frac{{ – 5 – 1}}{{0 – 4}}} \right) = \frac{6}{4} = \frac{3}{2}(1.5)\) (M1)(A1)
(M1) for gradient formula with correct substitution
Award (A1) for \(y = \frac{3}{2}x – 5\) with no other working
(iii) gradient of perpendicular is \( – \frac{2}{3}\) (A1)(ft) (C4)[4 marks]
\(\left( {\frac{{k + 2}}{{0 – 2}}} \right) = – \frac{2}{3}\), \(k = – \frac{2}{3}\) or \(y = – \frac{2}{3}x + c\), \(c = – \frac{2}{3}\therefore k = – \frac{2}{3}\) (M1)(A1)(ft)
Allow (\(0, – \frac{2}{3}\))
(M1) is for equating gradients or substituting gradient into \(y = mx + c\) (C2)[2 marks]
