Question
The function \(f(x)\) is such that \(f'(x) < 0\) for \(1 < x < 4\). At the point \({\text{P}}(4{\text{, }}2)\) on the graph of \(f(x)\) the gradient is zero.
a.Write down the equation of the tangent to the graph of \(f(x)\) at \({\text{P}}\).[2]
b.State whether \(f(4)\) is greater than, equal to or less than \(f(2)\).[2]
c.Given that \(f(x)\) is increasing for \(4 \leqslant x < 7\), what can you say about the point \({\text{P}}\)?[2]
▶️Answer/Explanation
Markscheme
\(y = 2\). (A1)(A1) (C2)
Note: Award (A1) for \(y = \ldots \), (A1) for \(2\).
Accept \(f(x) = 2\) and \(y = 0x + 2\)
Less (than). (A2) (C2)[2 marks]
Local minimum (accept minimum, smallest or equivalent) (A2) (C2)
Note: Award (A1) for stationary or turning point mentioned.
No mark is awarded for \({\text{gradient}} = 0\) as this is given in the question.
Question
The table given below describes the behaviour of f ′(x), the derivative function of f (x), in the domain −4 < x < 2.
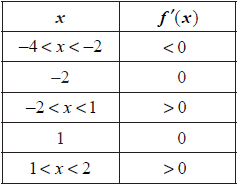
a.State whether f (0) is greater than, less than or equal to f (−2). Give a reason for your answer.[2]
b.The point P(−2, 3) lies on the graph of f (x).
Write down the equation of the tangent to the graph of f (x) at the point P.[2]
c.The point P(−2, 3) lies on the graph of f (x).
From the information given about f ′(x), state whether the point (−2, 3) is a maximum, a minimum or neither. Give a reason for your answer.[2]
▶️Answer/Explanation
Markscheme
greater than (A1)
Gradient between x = −2 and x = 0 is positive. (R1)
OR
The function is increased between these points or equivalent. (R1) (C2)
Note: Accept a sketch. Do not award (A1)(R0).[2 marks]
y = 3 (A1)(A1) (C2)
Note: Award (A1) for y = a constant, (A1) for 3.[2 marks]
minimum (A1)
Gradient is negative to the left and positive to the right or equivalent. (R1) (C2)
Note: Accept a sketch. Do not award (A1)(R0).[2 marks]
Question
\[f(x) = \frac{1}{3}{x^3} + 2{x^2} – 12x + 3\]
a.Find \(f'(x)\) .[3]
b.Find the interval of \(x\) for which \(f(x)\) is decreasing.[3]
▶️Answer/Explanation
Markscheme
\(f'(x) = {x^2} + 4x – 12\) (A1)(A1)(A1) (C3)
Notes: Award (A1) for each term. Award at most (A1)(A1)(A0) if other terms are seen.[3 marks]
\( – 6 \leqslant x \leqslant 2\) OR \( – 6 < x < 2\) (A1)(ft)(A1)(ft)(A1) (C3)
Notes: Award (A1)(ft) for \( – 6\), (A1)(ft) for \(2\), (A1) for consistent use of strict (\(<\)) or weak (\(\leqslant\)) inequalities. Final (A1) for correct interval notation (accept alternative forms). This can only be awarded when the left hand side of the inequality is less than the right hand side of the inequality. Follow through from their solutions to their \(f'(x) = 0\) only if working seen.[3 marks]
Question
Consider the graph of the function \(f(x) = {x^3} + 2{x^2} – 5\).
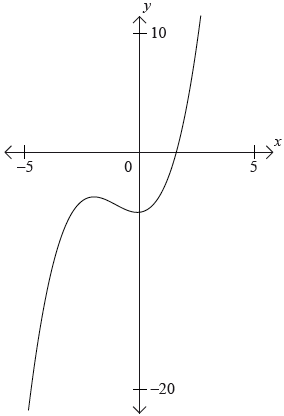
a.Label the local maximum as \({\text{A}}\) on the graph.[1]
b.Label the local minimum as B on the graph.[1]
c.Write down the interval where \(f'(x) < 0\).[1]
d.Draw the tangent to the curve at \(x = 1\) on the graph.[1]
e.Write down the equation of the tangent at \(x = 1\).[2]
▶️Answer/Explanation
Markscheme
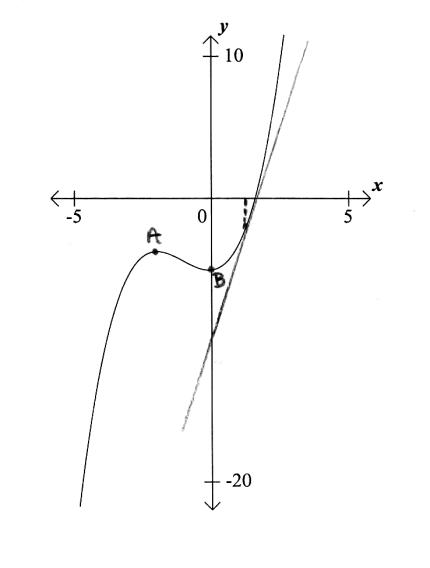
correct label on graph (A1) (C1)[1 mark]
correct label on graph (A1) (C1)[1 mark]
\( – 1.33 < x < 0\) \(\left( { – \frac{4}{3} < x < 0} \right)\) (A1) (C1)[1 mark]
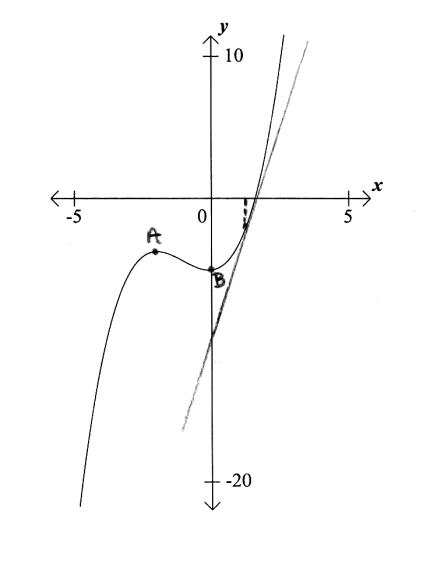
tangent drawn at \(x = 1\) on graph (A1) (C1)[1 mark]
\(y = 7x – 9\) (A1)(A1) (C2)
Notes: Award (A1) for \(7\), (A1) for \(-9\).
If answer not given as an equation award at most (A1)(A0).[2 marks]
