Question
The angle θ satisfies the equation tanθ + cotθ = 3. Find all the possible values of θ in \([0^o, 90^o]\).
▶️Answer/Explanation
Ans
METHOD 1
\(tanθ + \frac{1}{tanθ}=3 \Rightarrow tan^2θ-3 tanθ + 1 = 0\)
\(tanθ=\frac{3\pm\sqrt{5}}{2}\)
=0.382, 2.618
θ = 20.9o, 69.1o
METHOD 2
\(\frac{sinθ}{sinθ}+\frac{cosθ}{sinθ}=3\Rightarrow \frac{1}{sinθcosθ}=3\)
\(\Rightarrow \frac{1}{sin 2θ}=\frac{3}{2}\)
\(\Rightarrow sin 2θ=\frac{2}{3}\)
\(\Rightarrow θ=20.9^o, 69.1^o\)
Question
(a) Sketch the graph of y = cos(4x), in the interval 0≤x≤\(\pi\),
(b) On the same diagram sketch the graph of y=sec(4x), for 0≤x≤\(\pi\),
by indicating clearly the equations of any asymptotes.
(c) Use your sketch to solve
(i) the equation sec(4x)=-1, for 0≤x≤\(\pi\).
(ii) the inequality cos(4x)≤0, for 0≤x≤\(\pi\).
▶️Answer/Explanation
Ans
(a) and (b)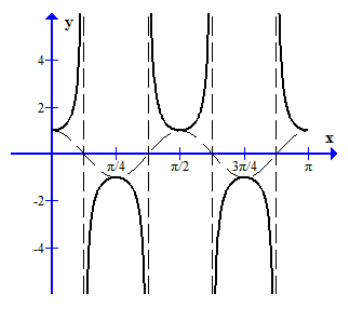
(c) (i) \(x=\frac{\pi}{4}, x=\frac{3\pi}{4}\) (ii) \(\frac{\pi}{8}≤x≤\frac{3\pi}{8}\) or \(\frac{5\pi}{8}≤x≤\frac{7\pi}{8}\).
Question
The diagram below shows the boundary of the cross-section of a water channel.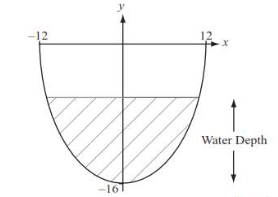
The equation that represents this boundary is y=16sec(\(\frac{\pi x}{36}\))-32 where x and y are both measured in cm.
The top of the channel is level with the ground and has a width of 24cm. The maximum depth of the channel is 16 cm.
Find the width of the water surface in the channel when the water depth is 10 cm. Give your answer in the form a arccosb where a,b ∈\(\mathbb{R}\).
▶️Answer/Explanation
Ans
10 cm water depth corresponds to 16sec(\(\frac{\pi x}{36}\)0=k or equivalent i.e. making a trigonometrical function the subject of the equation.
\(cos(\frac{\pi x}{36})=\frac{8}{13}\)
\(\frac{\pi x}{36}=\pm arccos\frac{8}{13}\)
Width of water surface is \(\frac{72}{\pi}\) arccos \(\frac{8}{13}\) (cm)
Question
Let f be the function f(x) = x arccos x + \(\frac{1}{2}x\) for -1≤x≤1 and g the funtion g(x) = cos 2x for -1≤x≤1.
(a) On the grid below, sketch the graph of f and of g.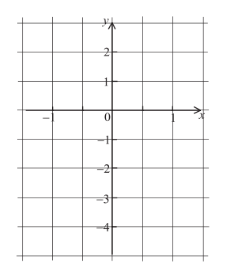
(b) Write down the solution of the equation f(x) = g(x). _______
(c) Write down the range of g. _______________
▶️Answer/Explanation
Ans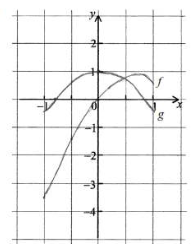
(b) x = 0.412
(c) Accept [-0.416,1] or [-0.416,1] or [cos2,1],[cos(-2),1].
Question
(a) Show that \(\arctan \left( {\frac{1}{2}} \right) + \arctan \left( {\frac{1}{3}} \right) = \frac{\pi }{4}\) .
(b) Hence, or otherwise, find the value of \(\arctan (2) + \arctan (3)\) .
▶️Answer/Explanation
Markscheme
(a) METHOD 1
let \(x = \arctan \frac{1}{2} \Rightarrow \tan x = \frac{1}{2}\) and \(y = \arctan \frac{1}{3} \Rightarrow \tan y = \frac{1}{3}\)
\(\tan (x + y) = \frac{{\tan x + \tan y}}{{1 – \tan x\tan y}} = \frac{{\frac{1}{2} + \frac{1}{3}}}{{1 – \frac{1}{2} \times \frac{1}{3}}} = 1\) M1
so, \(x + y = \arctan 1 = \frac{\pi }{4}\) A1AG
METHOD 2
for \(x,{\text{ }}y > 0\) , \(\arctan x + \arctan y = \arctan \left( {\frac{{x + y}}{{1 – xy}}} \right)\) if \(xy < 1\) M1
so, \(\arctan \frac{1}{2} + \arctan \frac{1}{3} = \arctan \left( {\frac{{\frac{1}{2} + \frac{1}{3}}}{{1 – \frac{1}{2} \times \frac{1}{3}}}} \right) = \frac{\pi }{4}\) A1AG
METHOD 3
an appropriate sketch M1
e.g. 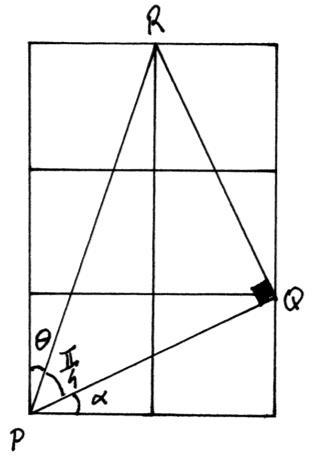
correct reasoning leading to \(\frac{\pi }{4}\) R1AG
(b) METHOD 1
\(\arctan (2) + \arctan (3) = \frac{\pi }{2} – \arctan \left( {\frac{1}{2}} \right) + \frac{\pi }{2} – \arctan \left( {\frac{1}{3}} \right)\) (M1)
\( = \pi – \left( {\arctan \left( {\frac{1}{2}} \right) + \arctan \left( {\frac{1}{3}} \right)} \right)\) (A1)
Note: Only one of the previous two marks may be implied.
\( = \pi – \frac{\pi }{4} = \frac{{3\pi }}{4}\) A1 N1
METHOD 2
let \(x = \arctan 2 \Rightarrow \tan x = 2\) and \(y = \arctan 3 \Rightarrow \tan y = 3\)
\(\tan (x + y) = \frac{{\tan x + \tan y}}{{1 – \tan x\tan y}} = \frac{{2 + 3}}{{1 – 2 \times 3}} = – 1\) (M1)
as \(\frac{\pi }{4} < x < \frac{\pi }{2}\,\,\,\,\,\left( {{\text{accept }}0 < x < \frac{\pi }{2}} \right)\)
and \(\frac{\pi }{4} < y < \frac{\pi }{2}\,\,\,\,\,\left( {{\text{accept }}0 < y < \frac{\pi }{2}} \right)\)
\(\frac{\pi }{2} < x + y < \pi \,\,\,\,\,{\text{(accept }}0 < x + y < \pi )\) (R1)
Note: Only one of the previous two marks may be implied.
so, \(x + y = \frac{{3\pi }}{4}\) A1 N1
METHOD 3
for \(x,{\text{ }}y > 0\) , \(\arctan x + \arctan y = \arctan \left( {\frac{{x + y}}{{1 – xy}}} \right) + \pi {\text{ if }}xy > 1\) (M1)
so, \(\arctan 2 + \arctan 3 = \arctan \left( {\frac{{2 + 3}}{{1 – 2 \times 3}}} \right) + \pi \) (A1)
Note: Only one of the previous two marks may be implied.
\( = \frac{{3\pi }}{4}\) A1 N1
METHOD 4
an appropriate sketch M1
e.g. 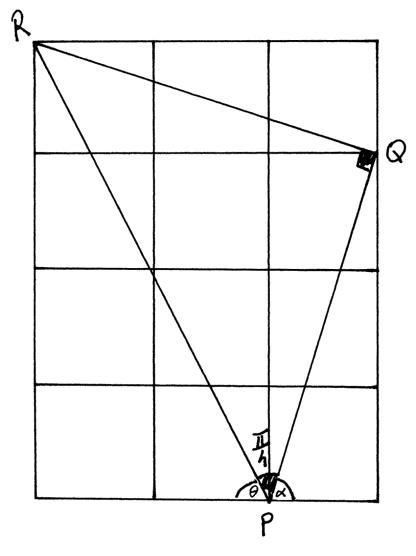
correct reasoning leading to \(\frac{{3\pi }}{4}\) R1A1
[5 marks]
Question
a.Consider the following functions:
\(h(x) = \arctan (x),{\text{ }}x \in \mathbb{R}\)
\(g(x) = \frac{1}{x}\), \(x\in \mathbb{R}\), \({\text{ }}x \ne 0\)
Sketch the graph of \(y = h(x)\).[2]
b.Find an expression for the composite function \(h \circ g(x)\) and state its domain.[2]
Given that \(f(x) = h(x) + h \circ g(x)\),
(i) find \(f'(x)\) in simplified form;
(ii) show that \(f(x) = \frac{\pi }{2}\) for \(x > 0\).[7]
Nigel states that \(f\) is an odd function and Tom argues that \(f\) is an even function.
(i) State who is correct and justify your answer.
(ii) Hence find the value of \(f(x)\) for \(x < 0\).[3]
▶️Answer/Explanation
Markscheme
a.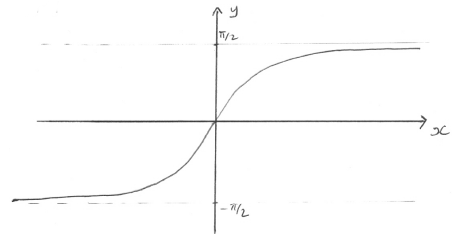 A1A1
A1A1
Note: A1 for correct shape, A1 for asymptotic behaviour at \(y = \pm \frac{\pi }{2}\).
[2 marks]
\(h \circ g(x) = \arctan \left( {\frac{1}{x}} \right)\) A1
domain of \(h \circ g\) is equal to the domain of \(g:x \in \circ ,{\text{ }}x \ne 0\) A1
[2 marks]
(i) \(f(x) = \arctan (x) + \arctan \left( {\frac{1}{x}} \right)\)
\(f'(x) = \frac{1}{{1 + {x^2}}} + \frac{1}{{1 + \frac{1}{{{x^2}}}}} \times – \frac{1}{{{x^2}}}\) M1A1
\(f'(x) = \frac{1}{{1 + {x^2}}} + \frac{{ – \frac{1}{{{x^2}}}}}{{\frac{{{x^2} + 1}}{{{x^2}}}}}\) (A1)
\( = \frac{1}{{1 + {x^2}}} – \frac{1}{{1 + {x^2}}}\)
\( = 0\) A1
(ii) METHOD 1
f is a constant R1
when \(x > 0\)
\(f(1) = \frac{\pi }{4} + \frac{\pi }{4}\) M1A1
\( = \frac{\pi }{2}\) AG
METHOD 2
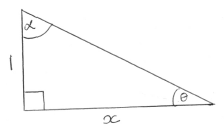
from diagram
\(\theta = \arctan \frac{1}{x}\) A1
\(\alpha = \arctan x\) A1
\(\theta + \alpha = \frac{\pi }{2}\) R1
hence \(f(x) = \frac{\pi }{2}\) AG
METHOD 3
\(\tan \left( {f(x)} \right) = \tan \left( {\arctan (x) + \arctan \left( {\frac{1}{x}} \right)} \right)\) M1
\( = \frac{{x + \frac{1}{x}}}{{1 – x\left( {\frac{1}{x}} \right)}}\) A1
denominator = 0, so \(f(x) = \frac{\pi }{2}{\text{ (for }}x > 0)\) R1
[7 marks]
(i) Nigel is correct. A1
METHOD 1
\(\arctan (x)\) is an odd function and \(\frac{1}{x}\) is an odd function
composition of two odd functions is an odd function and sum of two odd functions is an odd function R1
METHOD 2
\(f( – x) = \arctan ( – x) + \arctan \left( { – \frac{1}{x}} \right) = – \arctan (x) – \arctan \left( {\frac{1}{x}} \right) = – f(x)\)
therefore f is an odd function. R1
(ii) \(f(x) = – \frac{\pi }{2}\) A1
[3 marks]
Question
Solve the equations
(a) \(cos(2arcsinx)=0.68\), by applying a double angle identity.
(b) arctan x + arctan 2x = arctan \(\sqrt{2}\), by applying tan(A+B)
▶️Answer/Explanation
Ans
(a) \(1-2x^2=0.68 \Rightarrow … \Rightarrow x=0.4\) (b) \(\frac{2+2x}{1-2x^2}=\sqrt{2} \Rightarrow … \Rightarrow x=\frac{\sqrt{2}}{4}\)
Question
(a) Write down the domain and the range of the function f(x) = arctan x.
(b) By applying tan, find the values of
\(A=arctan\frac{1}{3}+arctan\frac{1}{2},\) \(B=arctan 2 + arctan 3\)
\(C=arctan\frac{1}{3}-arctan2\) \(D=arctan\frac{2}{3}+arctan\frac{3}{2}\)
▶️Answer/Explanation
Ans
(a) x∈R, \(-\frac{\pi}{2}<y<\frac{\pi}{2}\)
(b) \(tan A = 1 \Rightarrow A=\frac{\pi}{4}\) \(tan B=-1 \Rightarrow B=\frac{3\pi}{4}\) (B is +tive)
\(tan C=-1\Rightarrow C=-\frac{\pi}{4}\), (C is -tive) tan D not defined \(\Rightarrow D=\frac{\pi}{2}\)Questions 23-25 : without GDC.
Question
Solve \(tan^22θ=1\), in the interval \(-\frac{\pi}{2}≤θ≤\frac{\pi}{2}\)
▶️Answer/Explanation
Ans
\(tan^22\theta = 1\)
\(\Rightarrow tan 2\theta=\pm 1\)
\(\theta = \pm \frac{3\pi}{4},\pm \frac{\pi}{4}\)
\(\Rightarrow = \pm\frac{3\pi}{8},\pm\frac{\pi}{8}\) or \(\pm 1.18, \pm 0.393\)
Question
The function f is defined by f(x)=cosec x + tan 2x.
(a) Sketch the graph of f for \(-\frac{\pi}{2}≤x≤\frac{\pi}{2}\). Hence state
(i) the x-intercepts;
(ii) the equations of the asymtotes;
(ii) the coordinates of the maximum and minimum points.
(b) Show that the roots of f(x) = 0 satisfy the equation
\(2cos^3x-2cos^2x-2cos x+1=0\)
(c) Show that \(f(\pi-x)+f(\pi+x)=0\)
▶️Answer/Explanation
Ans
(a)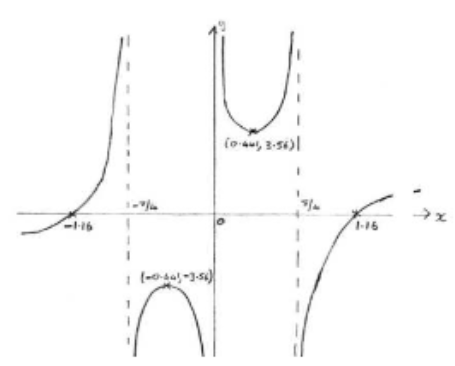
(i) x intercepts: -1.16, 1.16
(ii) Asymptotes: \(x=-\frac{\pi}{4},0,\frac{\pi}{4}\)
(iii) Max. point (-0.441,-3.56)
Min. point (0.441, 3.56)
(b) cosec x + tan 2x = 0
\(\Rightarrow \frac{1}{sin x}+\frac{sin 2x}{cos 2x}=0\)
\(\Rightarrow \frac{1}{sin x}+\frac{2sinx cosx}{2cos^2x-1}=0\)
\(\Rightarrow 2 cos^2x-1+2sin^2xcosx=0\)
\(\Rightarrow 2 cos^2x -1 +2cos x – 2cos^3 x=0\)
\(\Rightarrow 2 cos^3 x – 2cos%2x- 2 cosx + 1=0\)
(c)
\(f(\pi-x)=\frac{1}{sin(\pi-x)}+ tan (2\pi-2x)\)
\(=\frac{1}{sin x}- tan 2x\)
\(f(\pi+x)=\frac{1}{sin(\pi+x)}+tan(2\pi+2x)\)
\(=-\frac{1}{sin x}+tan 2x\)
Hence \(f(\pi-x)+f(\pi+x)=\frac{1}{sin x}-tan 2x-\frac{1}{sinx}+tan2=0\)
Question
(a) Sketch the curve f(x) = sin 2x, 0≤x≤\(\pi\).
(b) Hence sketch on a separate diagram the graph of g(x) = csc 2x, 0≤x≤\(\pi\), clearly stating the coordinates of any local maximum or minimum points and the equations of any asymptotes.
(c) Show that tan x + cot x = 2 csc 2x.
(d) Hence or otherwise, find the coordinates of the local maximum and local minimum ooints onthe graph of y = tan 2x + cot 2x, 0≤x≤\(\frac{\pi}{2}\).
(e) Find the solution of the equation csc 2x = 1.5 tan x – 0.5, 0≤x≤\(\frac{\pi}{2}\).
▶️Answer/Explanation
Ans
(a)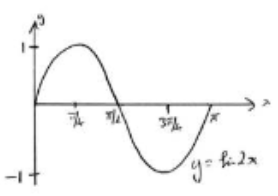
(b)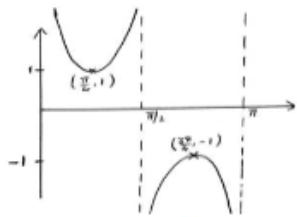
Asymptotes: \(x-0, x-\frac{\pi}{2},x-\pi\)
Max (\(\frac{3\pi}{4},-1\)), Min (\(\frac{\pi}{4},1\))
(c) \(tan x + cot x = \frac{sin x }{cos x}+\frac{cos x}{sin x}\)
\(=\frac{sin^2 x+ cos^2 x}{sinx cos x}\)
\(=\frac{1}{\frac{1}{2}sin2x}\)
\(=2csc2x\)
(d) tan 2x + cot 2x = 2 csc 4x
Max is at \((\frac{3\pi}{8},-2\))
Min is at (\(\frac{\pi}{8},2\))
(c) csc 2x = 1.5tan x – 0.5
\(\frac{1}{2} tan x+\frac{1}{2} cot x =\frac{3}{2} tanx – \frac{1}{2}\)
\(tan x + cot x = 3 tan x – 1\)
\(2 tan^2 x – tan x – 1=0\)
\((2 tan x + 1)(tan x – 1)=0\)
\(tan x = – \frac{1}{2}\) or 1
\(x=\frac{\pi}{4}\)
Question
(a) Sketch the graph of the function
\(C(x)=cos x +\frac{1}{2}cos 2x\) for -2\(\pi\)≤x≤2\(\pi\)
(b) Prove that the funciton C(x) is periodic and state its period
(c) For what values of x, 2\(\pi\)≤x≤2\(\pi\), is C(x) a maximum?
(d) Let x = xo be the smallest positive value of x for which C(x)=0. Find an approximate value of xo which is correct to two significant figures.
(e) (i) Prove that C(x) = C(-x) for all x.
(ii) Let x=x1 be that value of x,\(\pi\)<x<2\(\pi\), for which C(x) = 0. Find the value of x1 in terms of xo.
▶️Answer/Explanation
Ans
(a)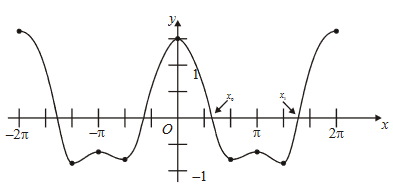
(b) \(C(x)=cos x +\frac{1}{2} cos 2x\)
\(C(x+2\pi)=cos(x+2\pi)+\frac{1}{2}cos(2x+4\pi)\)
\(=cos x+\frac{1}{2}cos2x\)
\(=C(x)\)
Therefore, C(x) is periodic with period 2\(\pi\).
(c) C(x) is a maximum for x = -2\(\pi\), 0, 2\(\pi\).
(d) \(x_0=1.2\) (using a graph display calculator)
(e) (i) \(C(-x)=cos(-x)+cos\frac{1}{2}(-2x)\)
\(=cos x +\frac{1}{2}cos2x\)
\(=C(x)\) for all x
(ii) \(C(x_o)=0\) so \(C(-x_o)=0[C(x)=C(-x)]\)
\(C(2\pi-x_o)=C(-x_o)=0\) [C(x) is periodic, period 2\(\pi\)]
Therefore, \(x_1=2\pi-x_o\)
Question
The function f with domain \([0,\frac{\pi}{2}]\) is defined by f(x) = cos x + \(\sqrt{3}\) sin x.
This function may also be expressed in the form \( R cos(x-\alpha)\) where R>0 and 0<\(\alpha <\frac{\pi}{2}\).
(a) Find the exact value of R and of \(\alpha\). [Hint: expand \(Rcos(x-\alpha)\) and compare with f]
(b) Find the range of the funciton f.
(c) Find the exact value of x satisfying the equation f(x)=\(\sqrt{2}\).
▶️Answer/Explanation
Ans
(a) \(cosx+\sqrt{3} sinx=Rcos \alpha cos x+R sin\alpha sin x\)
\(=>R cos\alpha = 1, R sin \alpha = \sqrt{3} = > R = 2, \alpha =\frac{\pi}{3}\)
(b) (i) Since f(x) = 2cos (x-\(\frac{\pi}{3})\).
\(f_{max}=2\) (when x = \(\frac{\pi}{3}\)); \(f_{min}=1\) (when x = 0)
Range is [1,2]
(c) \(f(x) = \sqrt{2}\) = > cos (x-\(\frac{\pi}{3})=\frac{\sqrt{2}{2}\)
\(x-\frac{\pi}{3}=\pm\frac{\pi}{4}\)
\(x=\frac{\pi}{12}\)
OR
\(f(x)=\sqrt{2}\)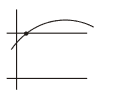
\(x=0.262 => x=\frac{\pi}{12}\)
