Question
Consider the complex numbers z1 = 1 + bi and z2 = (1 – b2) – 2bi, where b ∈ R, b ≠ 0.
(a) Find an expression for z1z2 in terms of b.
(b) Hence, given that arg (z1 z2) = \(\frac{\pi }{4}\) , find the value of b.
▶️Answer/Explanation
Ans:
(a)
z1z2 = (1 + bi) ((1-b2) – (2b)i)
= (1-b2 – 2i2b2) + i (-2b + b – b3)
= (1 + b2) + i (-b – b3)
Note: Award A1 for 1+ b2 and A1 for − bi – b3i .
(b) arg (z1z2) = arctan \(\left ( \frac{-b-b^{3}}{1 + b^{2}} \right )= \frac{\pi }{4}\)
EITHER
arctan (-b) = \(\frac{\pi }{4}\) (since 1+b2 ≠, 0 for b ∈ R)
OR
-b – b3 = 1 + b2 (or equivalent)
THEN
b =−1
Question
In the following Argand diagram, the points Z1 , O and Z2 are the vertices of triangle Z1OZ2 described anticlockwise.
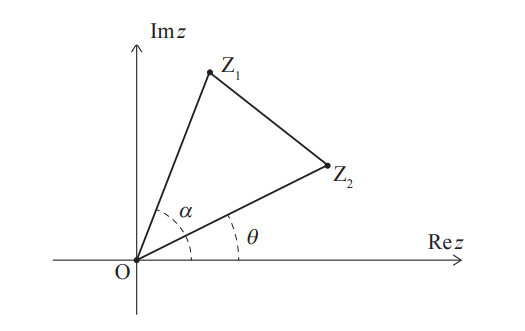
The point Z1 represents the complex number z1 = r1eiα , where r1 > 0. The point Z2 represents the complex number z2 = r2eiθ , where r2 > 0.
Angles α, θ are measured anticlockwise from the positive direction of the real axis such that 0 ≤ α, θ < 2π and 0 < α – θ < π.
(a) Show that z1z2 * = r1r2e i(α – θ) where z2* is the complex conjugate of z2 .
(b) Given that Re (z1 z2*) = 0, show that Z1OZ2 is a right-angled triangle.
In parts (c), (d) and (e), consider the case where Z1OZ2 is an equilateral triangle.
(c) (i) Express z1 in terms of z2 .
(ii) Hence show that z12 + z22 = z1 z2 .
Let z1 and z2 be the distinct roots of the equation z2 + az + b = 0 where z ∈ C and a , b ∈ R.
(d) Use the result from part (c)(ii) to show that a2 – 3b = 0.
Consider the equation z2 + az + 12 = 0, where z ∈ C and a ∈ R.
(e) Given that 0 < α – θ < π, deduce that only one equilateral triangle Z1OZ2 can be formed from the point O and the roots of this equation.
▶️Answer/Explanation
Ans:
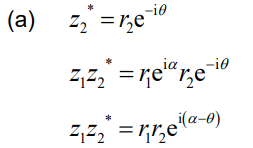
Note: Accept working in modulus-argument form
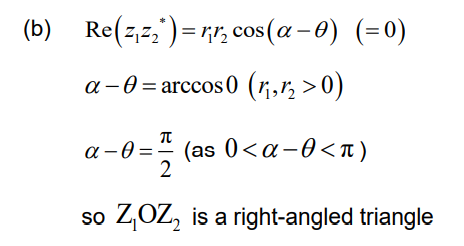
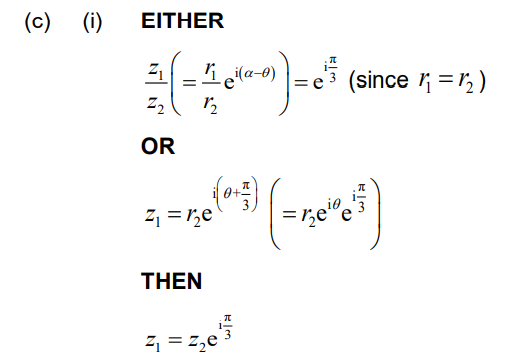
Note: Accept working in either modulus-argument form to obtain \(z_{1} = z_{2}\left ( cos\frac{\pi }{3} + isin\frac{\pi }{3} \right )\) or in Cartesian form to obtain \(z_{1} = z_{2}\left ( \frac{1}{2} + \frac{\sqrt{3}}{2} \right )i\)




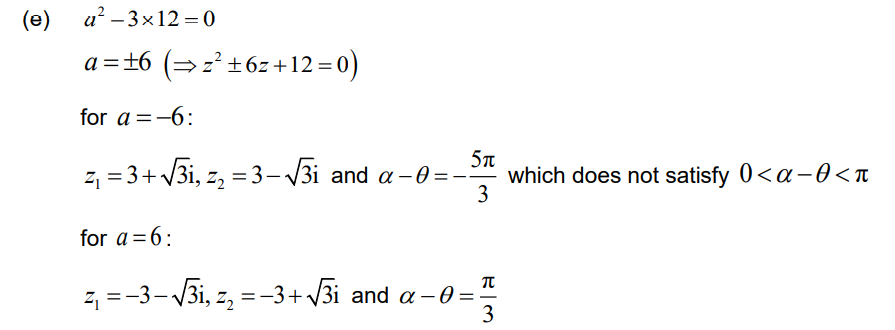
so (for 0 < α – θ < π), only one equilateral triangle can be formed from point O and the two roots of this equation
Question
Consider the complex numbers z1 = 1 + bi and z2 = (1 – b2) – 2bi, where b ∈ R, b ≠ 0.
(a) Find an expression for z1z2 in terms of b.
(b) Hence, given that arg (z1 z2) = \(\frac{\pi }{4}\) , find the value of b.
▶️Answer/Explanation
Ans:
(a)
z1z2 = (1 + bi) ((1-b2) – (2b)i)
= (1-b2 – 2i2b2) + i (-2b + b – b3)
= (1 + b2) + i (-b – b3)
Note: Award A1 for 1+ b2 and A1 for − bi – b3i .
(b) arg (z1z2) = arctan \(\left ( \frac{-b-b^{3}}{1 + b^{2}} \right )= \frac{\pi }{4}\)
EITHER
arctan (-b) = \(\frac{\pi }{4}\) (since 1+b2 ≠, 0 for b ∈ R)
OR
-b – b3 = 1 + b2 (or equivalent)
THEN
b =−1
Question
If \({z_1} = a + a\sqrt 3 i\) and \({z_2} = 1 – i\), where a is a real constant, express \({z_1}\) and \({z_2}\) in the form \(r\,{\text{cis}}\,\theta \), and hence find an expression for \({\left( {\frac{{{z_1}}}{{{z_2}}}} \right)^6}\) in terms of a and i.
▶️Answer/Explanation
Markscheme
\({z_1} = 2a{\text{cis}}\left( {\frac{\pi }{3}} \right){\text{, }}{z_2} = \sqrt 2 {\text{ cis}}\left( { – \frac{\pi }{4}} \right)\) M1 A1 A1
EITHER
\({\left( {\frac{{{z_1}}}{{{z_2}}}} \right)^6} = \frac{{{2^6}{a^6}{\text{cis(0)}}}}{{{{\sqrt 2 }^6}{\text{cis}}\left( {\frac{\pi }{2}} \right)}}\left( { = 8{a^6}{\text{cis}}\left( { – \frac{\pi }{2}} \right)} \right)\) M1 A1 A1
OR
\({\left( {\frac{{{z_1}}}{{{z_2}}}} \right)^6} = {\left( {\frac{{2a}}{{\sqrt 2 }}{\text{cis}}\left( {\frac{{7\pi }}{{12}}} \right)} \right)^6}\) M1 A1
\( = 8{a^6}{\text{cis}}\left( { – \frac{\pi }{2}} \right)\) A1
THEN
\( = – 8{a^6}{\text{i}}\) A1
Note: Accept equivalent angles, in radians or degrees.
Accept alternate answers without cis e.g. \({\text{ = }}\frac{{8{a^6}}}{{\text{i}}}\)
[7 marks]
Question
Given that z is the complex number \(x + {\text{i}}y\) and that \(\left| {\,z\,} \right| + z = 6 – 2{\text{i}}\) , find the value of x
and the value of y .
▶️Answer/Explanation
Markscheme
\(\sqrt {{x^2} + {y^2}} + x + y{\text{i}} = 6 – 2{\text{i}}\) (A1)
equating real and imaginary parts M1
\(y = – 2\) A1
\(\sqrt {{x^2} + 4} + x = 6\) A1
\({x^2} + 4 = {(6 – x)^2}\) M1
\( – 32 = – 12x \Rightarrow x = \frac{8}{3}\) A1
[6 marks]
Question
Given that \((4 – 5{\text{i}})m + 4n = 16 + 15{\text{i}}\) , where \({{\text{i}}^2} = – 1\), find m and n if
a.m and n are real numbers;[3]
b.m and n are conjugate complex numbers.[4]
▶️Answer/Explanation
Markscheme
attempt to equate real and imaginary parts M1
equate real parts: \(4m + 4n = 16\); equate imaginary parts: \( -5m = 15\) A1
\( \Rightarrow m = -3,{\text{ }}n = 7\) A1
[3 marks]
let \(m = x + {\text{i}}y,{\text{ }}n = x – {\text{i}}y\) M1
\( \Rightarrow (4 – 5{\text{i}})(x + {\text{i}}y) + 4(x – {\text{i}}y) = 16 + 15{\text{i}}\)
\( \Rightarrow 4x – 5{\text{i}}x + 4{\text{i}}y + 5y + 4x – 4{\text{i}}y = 16 + 15{\text{i}}\)
attempt to equate real and imaginary parts M1
\(8x + 5y = 16,{\text{ }} -5x = 15\) A1
\( \Rightarrow x = -3,{\text{ }}y = 8\) A1
\(( \Rightarrow m = -3 + 8{\text{i}},{\text{ }}n = -3 – 8{\text{i}})\)
[4 marks]
Question
a. Factorize \({z^3} + 1\) into a linear and quadratic factor.[2]
b. Let \(\gamma = \frac{{1 + {\text{i}}\sqrt 3 }}{2}\).
(i) Show that \(\gamma \) is one of the cube roots of −1.
(ii) Show that \({\gamma ^2} = \gamma – 1\).
(iii) Hence find the value of \({(1 – \gamma )^6}\).[9]
▶️Answer/Explanation
Markscheme
a.using the factor theorem z +1 is a factor (M1)
\({z^3} + 1 = (z + 1)({z^2} – z + 1)\) A1
[2 marks]
(i) METHOD 1
\({z^3} = – 1 \Rightarrow {z^3} + 1 = (z + 1)({z^2} – z + 1) = 0\) (M1)
solving \({z^2} – z + 1 = 0\) M1
\(z = \frac{{1 \pm \sqrt {1 – 4} }}{2} = \frac{{1 \pm {\text{i}}\sqrt 3 }}{2}\) A1
therefore one cube root of −1 is \(\gamma \) AG
METHOD 2
\({\gamma ^2} = \left( {{{\frac{{1 + i\sqrt 3 }}{2}}^2}} \right) = \frac{{ – 1 + i\sqrt 3 }}{2}\) M1A1
\({\gamma ^2} = \frac{{ – 1 + i\sqrt 3 }}{2} \times \frac{{1 + i\sqrt 3 }}{2} = \frac{{ – 1 – 3}}{4}\) A1
= −1 AG
METHOD 3
\(\gamma = \frac{{1 + i\sqrt 3 }}{2} = {e^{i\frac{\pi }{3}}}\) M1A1
\({\gamma ^3} = {e^{i\pi }} = – 1\) A1
(ii) METHOD 1
as \(\gamma \) is a root of \({z^2} – z + 1 = 0\) then \({\gamma ^2} – \gamma + 1 = 0\) M1R1
\(\therefore {\gamma ^2} = \gamma – 1\) AG
Note: Award M1 for the use of \({z^2} – z + 1 = 0\) in any way.
Award R1 for a correct reasoned approach.
METHOD 2
\({\gamma ^2} = \frac{{ – 1 + i\sqrt 3 }}{2}\) M1
\(\gamma – 1 = \frac{{1 + i\sqrt 3 }}{2} – 1 = \frac{{ – 1 + i\sqrt 3 }}{2}\) A1
(iii) METHOD 1
\({(1 – \gamma )^6} = {( – {\gamma ^2})^6}\) (M1)
\( = {(\gamma )^{12}}\) A1
\( = {({\gamma ^3})^4}\) (M1)
\( = {( – 1)^4}\)
\( = 1\) A1
METHOD 2
\({(1 – \gamma )^6}\)
\( = 1 – 6\gamma + 15{\gamma ^2} – 20{\gamma ^3} + 15{\gamma ^4} – 6{\gamma ^5} + {\gamma ^6}\) M1A1
Note: Award M1 for attempt at binomial expansion.
use of any previous result e.g. \( = 1 – 6\gamma + 15{\gamma ^2} + 20 – 15\gamma + 6{\gamma ^2} + 1\) M1
= 1 A1
Note: As the question uses the word ‘hence’, other methods that do not use previous results are awarded no marks.
[9 marks]
