Question
Consider the function f defined by f (x) = ln (x2 – 16) for x > 4 .
The following diagram shows part of the graph of f which crosses the x-axis at point A, with
coordinates ( a , 0 ). The line L is the tangent to the graph of f at the point B.
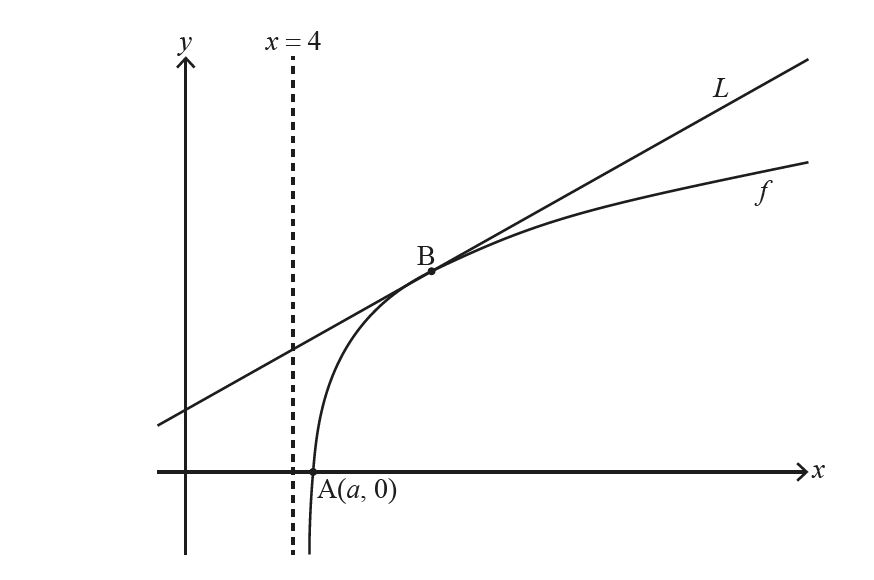
(a) Find the exact value of a . [3]
(b) Given that the gradient of L is \(\frac{1}{3}\) , find the x-coordinate of B. [6]
▶️Answer/Explanation
Ans:
(a) When f(x)=0, we have
ln(x2−16)=0
x2−16=1
x=±√17
However, since x>4, we have x=√17
(b) Differentiating f(x) with respect to x, we have f′(x)= \(\frac{2x}{x^2-16}\)
At B, f′(x)=\(\frac{1}{3}\) , i.e., we have
x2−16=6x
x2−6x−16=0
(x+2)(x−8)=0.
Thus, x=−2 (reject) or x=8.
Question
Solve the equation \(2 – {\log _3}(x + 7) = {\log _{\tfrac{1}{3}}}2x\) .
▶️Answer/Explanation
Markscheme
\({\log _3}\left( {\frac{9}{{x + 7}}} \right) = {\log _3}\frac{1}{{2x}}\) M1M1A1
Note: Award M1 for changing to single base, M1 for incorporating the 2 into a log and A1 for a correct equation with maximum one log expression each side.
\(x + 7 = 18x\) M1
\(x = \frac{7}{{17}}\) A1 [5 marks]
Question
The first terms of an arithmetic sequence are \(\frac{1}{{{{\log }_2}x}},{\text{ }}\frac{1}{{{{\log }_8}x}},{\text{ }}\frac{1}{{{{\log }_{32}}x}},{\text{ }}\frac{1}{{{{\log }_{128}}x}},{\text{ }} \ldots \)
Find x if the sum of the first 20 terms of the sequence is equal to 100.
▶️Answer/Explanation
Markscheme
METHOD 1
\(d = \frac{1}{{{{\log }_8}x}} – \frac{1}{{{{\log }_2}x}}\) (M1)
\( = \frac{{{{\log }_2}8}}{{{{\log }_2}x}} – \frac{1}{{{{\log }_2}x}}\) (M1)
Note: Award this M1 for a correct change of base anywhere in the question.
\( = \frac{2}{{{{\log }_2}x}}\) (A1)
\(\frac{{20}}{2}\left( {2 \times \frac{1}{{{{\log }_2}x}} + 19 \times \frac{2}{{{{\log }_2}x}}} \right)\) M1
\( = \frac{{400}}{{{{\log }_2}x}}\) (A1)
\(100 = \frac{{400}}{{{{\log }_2}x}}\)
\({\log _2}x = 4 \Rightarrow x = {2^4} = 16\) A1
METHOD 2
\({20^{{\text{th}}}}{\text{ term}} = \frac{1}{{{{\log }_{{2^{39}}}}x}}\) A1
\(100 = \frac{{20}}{2}\left( {\frac{1}{{{{\log }_2}x}} + \frac{1}{{{{\log }_{{2^{39}}}}x}}} \right)\) M1
\(100 = \frac{{20}}{2}\left( {\frac{1}{{{{\log }_2}x}} + \frac{{{{\log }_2}{2^{39}}}}{{{{\log }_2}x}}} \right)\) M1(A1)
Note: Award this M1 for a correct change of base anywhere in the question.
\(100 = \frac{{400}}{{{{\log }_2}x}}\) (A1)
\({\log _2}x = 4 \Rightarrow x = {2^4} = 16\) A1
METHOD 3
\(\frac{1}{{{{\log }_2}x}} + \frac{1}{{{{\log }_8}x}} + \frac{1}{{{{\log }_{32}}x}} + \frac{1}{{{{\log }_{128}}x}} + \ldots \)
\(\frac{1}{{{{\log }_2}x}} + \frac{{{{\log }_2}8}}{{{{\log }_2}x}} + \frac{{{{\log }_2}32}}{{{{\log }_2}x}} + \frac{{{{\log }_2}128}}{{{{\log }_2}x}} + \ldots \) (M1)(A1)
Note: Award this M1 for a correct change of base anywhere in the question.
\( = \frac{1}{{{{\log }_2}x}}(1 + 3 + 5 + \ldots )\) A1
\( = \frac{1}{{{{\log }_2}x}}\left( {\frac{{20}}{2}(2 + 38)} \right)\) (M1)(A1)
\(100 = \frac{{400}}{{{{\log }_2}x}}\)
\({\log _2}x = 4 \Rightarrow x = {2^4} = 16\) A1 [6 marks]
Question
Solve the equation \({4^{x – 1}} = {2^x} + 8\).
▶️Answer/Explanation
Markscheme
\({2^{2x – 2}} = {2^x} + 8\) (M1)
\(\frac{1}{4}{2^{2x}} = {2^x} + 8\) (A1)
\({2^{2x}} – 4 \times {2^x} – 32 = 0\) A1
\(({2^x} – 8)({2^x} + 4) = 0\) (M1)
\({2^x} = 8 \Rightarrow x = 3\) A1
Notes: Do not award final A1 if more than 1 solution is given.
[5 marks]
Question
Consider \(a = {\log _2}3 \times {\log _3}4 \times {\log _4}5 \times \ldots \times {\log _{31}}32\). Given that \(a \in \mathbb{Z}\), find the value of a.
▶️Answer/Explanation
Markscheme
\(\frac{{\log 3}}{{\log 2}} \times \frac{{\log 4}}{{\log 3}} \times \ldots \times \frac{{\log 32}}{{\log 31}}\) M1A1
\( = \frac{{\log 32}}{{\log 2}}\) A1
\( = \frac{{5\log 2}}{{\log 2}}\) (M1)
\( = 5\) A1
hence \(a = 5\)
Note: Accept the above if done in a specific base eg \({\log _2}x\).
[5 marks]
