Question: [Maximum mark: 6]
Consider the function f(x) = \(2^{x} – \frac{1}{2^{x}},\) x ∈ R.
(a) Show that f is an odd function.
The function g is given by g(x) = \(\frac{x-1}{x^{2}-2x-3},\) where x ∈ R, x ≠ -1 , x ≠ 3.
(b) Solve the inequality f (x) ≥ g(x).
▶️Answer/Explanation
Ans:
(a) attempt to replace x with −x
f(-x) = \(2^{-x}-\frac{1}{2^{-x}}\)
EITHER
\(=\frac{1}{2^{x}}-2^{x} = -f(x)\)
OR
\(=-\left (2^{x} \frac{1}{2^{x}} \right )\left ( =-f(x) \right )\)
Note: Award M1A0 for a graphical approach including evidence that either the graph is invariant after rotation by 180°about the origin or the graph is invariant after a reflection in the
y -axis and then in the x -axis (or vice versa).
so f is an odd function
(b) attempt to find at least one intersection point
x = -1.26686….., x = 0.177935…..,x = 3.06167
x = -1.27, x = 0.178, x = 3.06
-1.27 ≤ x < – 1,
0.178 ≤ x < 3,
x ≥ 3.06
Question: [Maximum mark: 8]
A function f is defined by f ( x ) = \(x\sqrt{1-x^{2}} where -1\leq x\leq 1.\)
The graph of y = f (x) is shown below.
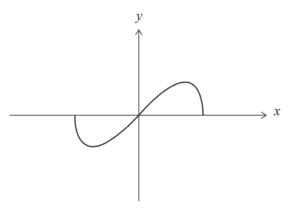
(a) Show that f is an odd function.
The range of f is a ≤ y ≤ b , where a, b ∈ R.
(b) Find the value of a and the value of b.
▶️Answer/Explanation
Ans:
(a) attempts to replace x with –x
\(f(-x) = -x\sqrt{1-(-x)^{2}}\)
\(= -x\sqrt{1-(-x)^{2}} \left ( =-f(x) \right )\)
Note: Award M1A1 for an attempt to calculate both f (-x ) and – f (-x) independently, showing that they are equal.
Note: Award M1A0 for a graphical approach including evidence that either the graph is invariant after rotation by 180° about the origin or the graph is invariant after a reflection in the y-axis and then in the x-axis (or vice versa).
so f is an odd function
(b) attempts both product rule and chain rule differentiation to find f¢(x)
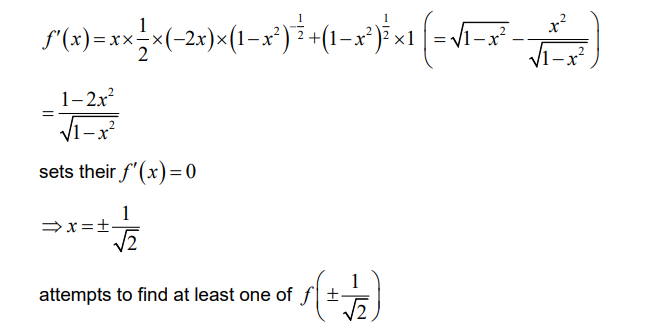
Note: Award M1 for an attempt to evaluate f(x) at least at one of their f¢(x) = 0 roots.
\(a = -\frac{1}{2} and b = \frac{1}{2}\)
Note: Award A1 for \(-\frac{1}{2}\leq y\leq \frac{1}{2}.\)
Question: [Maximum mark: 8]
A function f is defined by f ( x ) = \(x\sqrt{1-x^{2}} where -1\leq x\leq 1.\)
The graph of y = f (x) is shown below.

(a) Show that f is an odd function.
The range of f is a ≤ y ≤ b , where a, b ∈ R.
(b) Find the value of a and the value of b.
▶️Answer/Explanation
Ans:
(a) attempts to replace x with –x
\(f(-x) = -x\sqrt{1-(-x)^{2}}\)
\(= -x\sqrt{1-(-x)^{2}} \left ( =-f(x) \right )\)
Note: Award M1A1 for an attempt to calculate both f (-x ) and – f (-x) independently, showing that they are equal.
Note: Award M1A0 for a graphical approach including evidence that either the graph is invariant after rotation by 180° about the origin or the graph is invariant after a reflection in the y-axis and then in the x-axis (or vice versa).
so f is an odd function
(b) attempts both product rule and chain rule differentiation to find f¢(x)
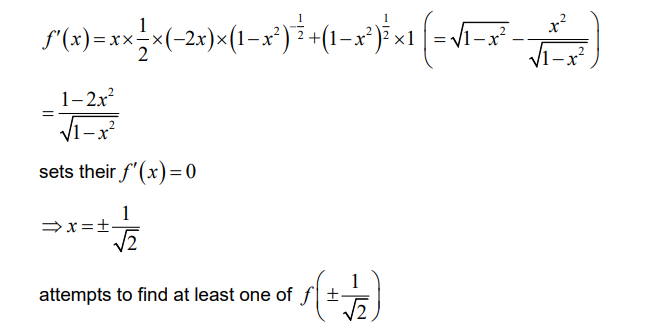
Note: Award M1 for an attempt to evaluate f(x) at least at one of their f¢(x) = 0 roots.
\(a = -\frac{1}{2} and b = \frac{1}{2}\)
Note: Award A1 for \(-\frac{1}{2}\leq y\leq \frac{1}{2}.\)
Question
A function f is defined by \(f(x)=arcsin\frac{x^2-1}{x^2+1},\;x\in \mathbb{R}\)
(a) Show that f is an even function. [1]
(b) By considering limits, show that the graph of y = f (x) has a horizontal asymptote and state its equation. [2]
(c) (i) Show that \(f{}'(x)=\frac{2x}{\sqrt{x^2}(x^2+1)} \; for\; x\in \mathbb{R},\;x\neq 0\)
(ii) By using the expression for f ′(x) and the result \(\sqrt{x^2}=\left | x \right |\) show that f is decreasing for x < 0 . [9]
A function g is defined by \(g(x)=arcsin\frac{x^2-1}{x^2+1},\;x\in \mathbb{R},\;x\geq 0.\)
(d) Find an expression for g-1(x) , justifying your answer. [5]
(e) State the domain of g-1 . [1]
(f) Sketch the graph of y = g-1(x) , clearly indicating any asymptotes with their equations and stating the values of any axes intercepts. [3]
▶️Answer/Explanation
Ans:
(a) Since $$\begin{eqnarray} f\left(-x\right) &=& \arcsin\left[\frac{\left(-x\right)^2-1}{\left(-x\right)^2+1}\right] \nonumber \\ &=& \arcsin\left(\frac{x^2-1}{x^2+1}\right) \nonumber \\ &=& f\left(x\right), \nonumber \\ \end{eqnarray}$$ $f$ is an even function.
(b) Consider $\lim_{x\to\infty} \arcsin\left(\frac{x^2-1}{x^2+1}\right)$, we have $$\begin{eqnarray} \lim_{x\to\infty} \arcsin\left(\frac{x^2-1}{x^2+1}\right) &=& \lim_{x\to\infty} \arcsin\left(\frac{1-\frac{1}{x^2}}{1+\frac{1}{x^2}}\right) \nonumber \\ &=& \arcsin\left(1\right) \nonumber \\ &=& \frac{\pi}{2}, \end{eqnarray}$$ i.e., $y=\frac{\pi}{2}$ is a horizontal asymptote.
(c)(i) Taking sine on both sides of $\arcsin\left(\frac{x^2-1}{x^2+1}\right)$, we have $\sin\left[f\left(x\right)\right]=\frac{x^2-1}{x^2+1}$.
Differentiating both sides with respect to $x$, we have $$\begin{eqnarray} f’\left(x\right)\cos\left[f\left(x\right)\right]=\frac{2x\left(x^2+1\right)-2x\left(x^2-1\right)}{\left(x^2+1\right)^2}. \end{eqnarray}$$ Rearranging, we have $$\begin{eqnarray} f’\left(x\right) &=& \frac{4x}{\left(x^2+1\right)^2}\times\frac{1}{\cos\left[f\left(x\right)\right]} \nonumber \\ &=& \frac{4x}{\left(x^2+1\right)^2}\times\frac{x^2+1}{2\sqrt{x^2}} \nonumber \\ &=& \frac{2x}{\sqrt{x^2}\left(x^2+1\right)}, \end{eqnarray}$$ since by Pythagoras’ Theorem, we can find $\cos\left[f\left(x\right)\right]=\frac{2\sqrt{x^2}}{x^2+1}$.
(c)(ii) When $x\lt 0$, $\sqrt{x^2}=\left|x\right|\gt 0$ and $x^2+1\gt 0$. Thus, $$\begin{eqnarray} \frac{2x}{\sqrt{x^2}\left(x^2+1\right)} \lt 0, \end{eqnarray}$$ i.e., $f$ is decreasing for $x\lt 0$.
(d) Let $y=\arcsin\left(\frac{x^2-1}{x^2+1}\right)$, then making $x$ the subject, we have $$\begin{eqnarray} \sin y=\frac{x^2-1}{x^2+1} \nonumber \\ \sin y\left(x^2+1\right) = x^2-1 \nonumber \\ x^2\left(\sin y-1\right) = -1-\sin y \nonumber \\ x^2 = \frac{1+\sin y}{1-\sin y} \nonumber \\ x = \pm\sqrt{\frac{1+\sin y}{1-\sin y}}. \end{eqnarray}$$ Since $x\geq 0$, $g^{-1}\left(x\right)=\sqrt{\frac{1+\sin x}{1-\sin x}}$.
(e) $\text{D}_{g^{-1}}=\text{R}_g=\left[-\frac{\pi}{2},\frac{\pi}{2}\right)$.
(f) (graph to be added in later)
Question
Consider the following functions:
\(h(x) = \arctan (x),{\text{ }}x \in \mathbb{R}\)
\(g(x) = \frac{1}{x}\), \(x\in \mathbb{R}\), \({\text{ }}x \ne 0\)
Sketch the graph of \(y = h(x)\).[2]
Find an expression for the composite function \(h \circ g(x)\) and state its domain.[2]
Given that \(f(x) = h(x) + h \circ g(x)\),
(i) find \(f'(x)\) in simplified form;
(ii) show that \(f(x) = \frac{\pi }{2}\) for \(x > 0\).[7]
Nigel states that \(f\) is an odd function and Tom argues that \(f\) is an even function.
(i) State who is correct and justify your answer.
(ii) Hence find the value of \(f(x)\) for \(x < 0\).[3]
▶️Answer/Explanation
Markscheme
A1A1
Note: A1 for correct shape, A1 for asymptotic behaviour at \(y = \pm \frac{\pi }{2}\).
[2 marks]
\(h \circ g(x) = \arctan \left( {\frac{1}{x}} \right)\) A1
domain of \(h \circ g\) is equal to the domain of \(g:x \in \circ ,{\text{ }}x \ne 0\) A1
[2 marks]
(i) \(f(x) = \arctan (x) + \arctan \left( {\frac{1}{x}} \right)\)
\(f'(x) = \frac{1}{{1 + {x^2}}} + \frac{1}{{1 + \frac{1}{{{x^2}}}}} \times – \frac{1}{{{x^2}}}\) M1A1
\(f'(x) = \frac{1}{{1 + {x^2}}} + \frac{{ – \frac{1}{{{x^2}}}}}{{\frac{{{x^2} + 1}}{{{x^2}}}}}\) (A1)
\( = \frac{1}{{1 + {x^2}}} – \frac{1}{{1 + {x^2}}}\)
\( = 0\) A1
(ii) METHOD 1
f is a constant R1
when \(x > 0\)
\(f(1) = \frac{\pi }{4} + \frac{\pi }{4}\) M1A1
\( = \frac{\pi }{2}\) AG
METHOD 2
from diagram
\(\theta = \arctan \frac{1}{x}\) A1
\(\alpha = \arctan x\) A1
\(\theta + \alpha = \frac{\pi }{2}\) R1
hence \(f(x) = \frac{\pi }{2}\) AG
METHOD 3
\(\tan \left( {f(x)} \right) = \tan \left( {\arctan (x) + \arctan \left( {\frac{1}{x}} \right)} \right)\) M1
\( = \frac{{x + \frac{1}{x}}}{{1 – x\left( {\frac{1}{x}} \right)}}\) A1
denominator = 0, so \(f(x) = \frac{\pi }{2}{\text{ (for }}x > 0)\) R1
[7 marks]
(i) Nigel is correct. A1
METHOD 1
\(\arctan (x)\) is an odd function and \(\frac{1}{x}\) is an odd function
composition of two odd functions is an odd function and sum of two odd functions is an odd function R1
METHOD 2
\(f( – x) = \arctan ( – x) + \arctan \left( { – \frac{1}{x}} \right) = – \arctan (x) – \arctan \left( {\frac{1}{x}} \right) = – f(x)\)
therefore f is an odd function. R1
(ii) \(f(x) = – \frac{\pi }{2}\) A1
[3 marks]
Question
The functions \(f\) and \(g\) are defined by \(f(x) = a{x^2} + bx + c,{\text{ }}x \in \mathbb{R}\) and \(g(x) = p\sin x + qx + r,{\text{ }}x \in \mathbb{R}\) where \(a,{\text{ }}b,{\text{ }}c,{\text{ }}p,{\text{ }}q,{\text{ }}r\) are real constants.
Given that \(f\) is an even function, show that \(b = 0\).[2]
Given that \(g\) is an odd function, find the value of \(r\).[2]
The function \(h\) is both odd and even, with domain \(\mathbb{R}\).
Find \(h(x)\).[2]
▶️Answer/Explanation
Markscheme
EITHER
\(f( – x) = f(x)\) M1
\( \Rightarrow a{x^2} – bx + c = a{x^2} + bx + c \Rightarrow 2bx = 0,{\text{ }}(\forall x \in \mathbb{R})\) A1
OR
\(y\)-axis is eqn of symmetry M1
so \(\frac{{ – b}}{{2a}} = 0\) A1
THEN
\( \Rightarrow b = 0\) AG
[2 marks]
\(g( – x) = – g(x) \Rightarrow p\sin ( – x) – qx + r = – p\sin x – qx – r\)
\( \Rightarrow – p\sin x – qx + r = – p\sin x – qx – r\) M1
Note: M1 is for knowing properties of sin.
\( \Rightarrow 2r = 0 \Rightarrow r = 0\) A1
Note: In (a) and (b) allow substitution of a particular value of \(x\)
[2 marks]
\(h( – x) = h(x) = – h(x) \Rightarrow 2h(x) = 0 \Rightarrow h(x) = 0,{\text{ }}(\forall x)\) M1A1
Note: Accept geometrical explanations.
[2 marks]
Total [6 marks]
