Question
Consider the function f defined by f (x) = 90e-0.5x for x ∈ R+ The graph of f and the line y = x intersect at point P.
Find the x-coordinate of P. [2]
The line L has a gradient of –1 and is a tangent to the graph of f at the point Q.
Find the exact coordinates of Q. [4]
Show that the equation of L is y = -x + 2ln45 + 2 . [2]
The shaded region A is enclosed by the graph of f and the lines y = x and L .
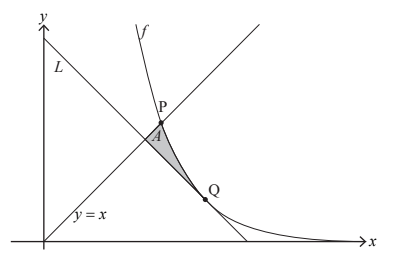
(i) Find the x-coordinate of the point where L intersects the line y = x .
(ii) Hence, find the area of A . [5]
The line L is tangent to the graphs of both f and the inverse function f –1 .
Find the shaded area enclosed by the graphs of f and f –1 and the line L . [2]
▶️Answer/Explanation
Ans:
(a)
attempt to find the point of intersection of the graph of f and the line y = x
x = 5.56619… = 5.57
(b)
\(f'(x)=-45e^{-0.5x}\)
attempt to set the gradient of equal to -1
-45e -0.5x = -1
Q has coordinates \((2ln45,2) \)or \((-2 ln\frac{1}{45},2)\)
(c)
attempt to substitute coordinates of Q ( in any order) into an appropriate equation
y-2= -(x-2ln45)
OR
2= – 2 ln 45 + C
equation of L is y = – x+ 2ln 45 + 2
(d)
(i) x= ln45 + 1 (=4.81)
(ii) appropriate method to find the sum of two areas using integrals of the difference of two functions 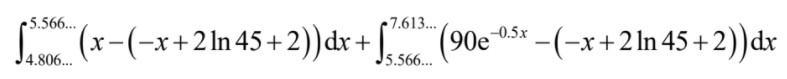
=1.51965… =1.52
(e) by symmetry 2 ×1.52
= 3.03930… = 3.04
Question
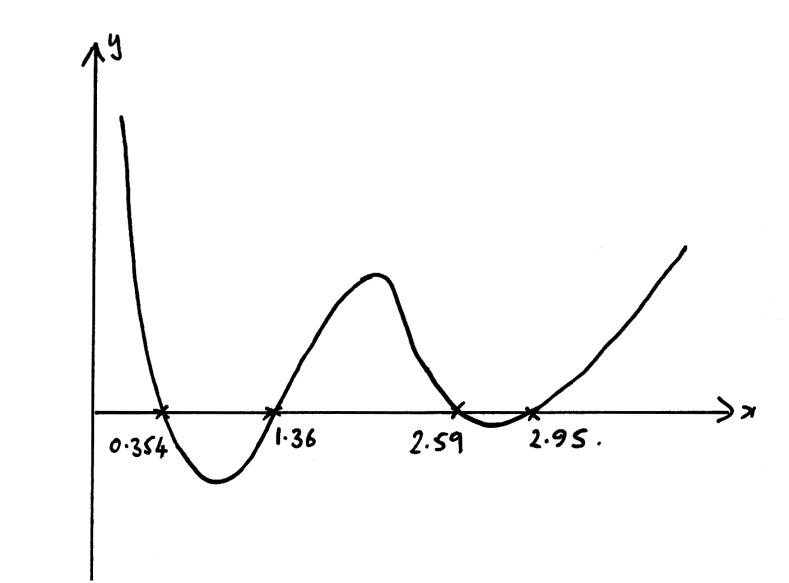
(a) Sketch the curve \(y = \left| {\ln x} \right| – \left| {\cos x} \right| – 0.1\) , \(0 < x < 4\) showing clearly the coordinates of the points of intersection with the x-axis and the coordinates of any local maxima and minima.
(b) Find the values of x for which \(\left| {\ln x} \right| > \left| {\cos x} \right| + 0.1\), \(0 < x < 4\) .
▶️Answer/Explanation
Markscheme
(a)
 A1
A1
Note: Award A1 for shape.
x-intercepts 0.354, 1.36, 2.59, 2.95 A2
Note: Award A1 for three correct, A0 otherwise.
maximum = (1.57, 0.352) = \(\left( {\frac{\pi }{2},0.352} \right)\) A1
minimum = (1, – 0.640) and (2.77, – 0.0129) A1
(b) \(0 < x < 0.354,{\text{ }}1.36 < x < 2.59,{\text{ }}2.95 < x < 4\) A2
Note: Award A1 if two correct regions given.
[7 marks]
Examiners report
Solutions to this question were extremely disappointing with many candidates doing the sketch in degree mode instead of radian mode. The two adjacent intercepts at 2.59 and 2.95 were often missed due to an unsatisfactory window. Some sketches were so small that a magnifying glass was required to read some of the numbers; candidates would be well advised to draw sketches large enough to be easily read.
Question
The diagram shows the graphs of a linear function f and a quadratic function g.
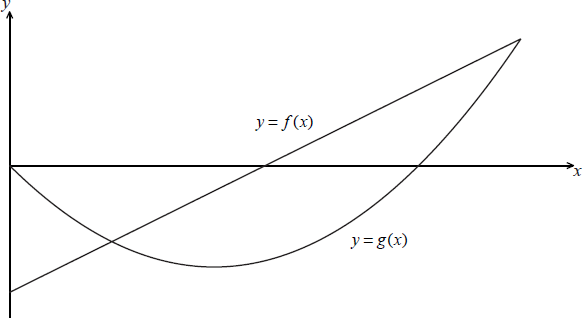
On the same axes sketch the graph of \(\frac{f}{g}\). Indicate clearly where the x-intercept and the asymptotes occur.
▶️Answer/Explanation
Markscheme
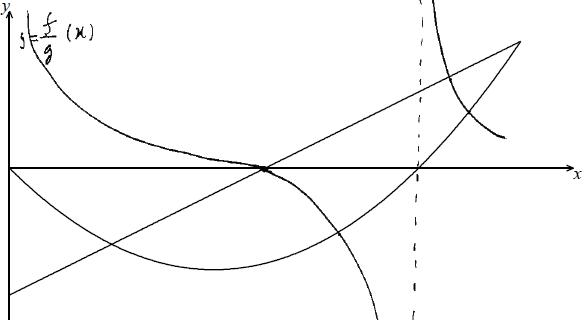
correct concavities A1A1
Note: Award A1 for concavity of each branch of the curve.
correct x-intercept of \(\frac{f}{g}\) (which is EXACTLY the x-intercept of f) A1
correct vertical asymptotes of \(\frac{f}{g}\) (which ONLY occur when x equals the x-intercepts of g) A1A1
[5 marks]
Examiners report
Many candidates answered well this question. Full marks were often achieved. Many other candidates did not attempt it at all.
Question
The function \(f(x) = 3\sin x + 4\cos x\) is defined for \(0 < x < 2\pi \) .
a.Write down the coordinates of the minimum point on the graph of f .[1]
b.The points \({\text{P}}(p,{\text{ }}3)\) and \({\text{Q}}(q,{\text{ }}3){\text{, }}q > p\), lie on the graph of \(y = f(x)\) .
Find p and q .[2]
c.Find the coordinates of the point, on \(y = f(x)\) , where the gradient of the graph is 3.[4]
d.Find the coordinates of the point of intersection of the normals to the graph at the points P and Q.[7]
▶️Answer/Explanation
Markscheme
\((3.79, – 5)\) A1
[1 mark]
\(p = 1.57{\text{ or }}\frac{\pi }{2},{\text{ }}q = 6.00\) A1A1
[2 marks]
\(f'(x) = 3\cos x – 4\sin x\) (M1)(A1)
\(3\cos x – 4\sin x = 3 \Rightarrow x = 4.43…\) (A1)
\((y = -4)\) A1
Coordinates are \((4.43, -4)\)
[4 marks]
\({m_{{\text{normal}}}} = \frac{1}{{{m_{{\text{tangent}}}}}}\) (M1)
gradient at P is \( – 4\) so gradient of normal at P is \(\frac{1}{4}\) (A1)
gradient at Q is 4 so gradient of normal at Q is \( – \frac{1}{4}\) (A1)
equation of normal at P is \(y – 3 = \frac{1}{4}(x – 1.570…){\text{ }}({\text{or }}y = 0.25x + 2.60…)\) (M1)
equation of normal at Q is \(y – 3 = \frac{1}{4}(x – 5.999…){\text{ }}({\text{or }}y = -0.25x + \underbrace {4.499…}_{})\) (M1)
Note: Award the previous two M1 even if the gradients are incorrect in \(y – b = m(x – a)\) where \((a,b)\) are coordinates of P and Q (or in \(y = mx + c\) with c determined using coordinates of P and Q.
intersect at \((3.79,{\text{ }}3.55)\) A1A1
Note: Award N2 for 3.79 without other working.
[7 marks]
