Question: [Maximum mark: 8]
A function f is defined by f(x) = \(\frac{2x – 1}{x + 1}\), where x ∈ R, x ≠ -1.
(a) The graph of y = f (x) has a vertical asymptote and a horizontal asymptote.
Write down the equation of
(i) the vertical asymptote;
(ii) the horizontal asymptote.
(b) On the set of axes below, sketch the graph of y = f (x) .
On your sketch, clearly indicate the asymptotes and the position of any points of intersection with the axes.
(c) Hence, solve the inequality \(0<\frac{2x – 1}{x + 1} <2.\)
(d) Solve the inequality \(0<\frac{2|x|-1}{|x| + 1} <2.\)
▶️Answer/Explanation
Ans:
(a) (i) x =−1
(ii) y = 2
(b)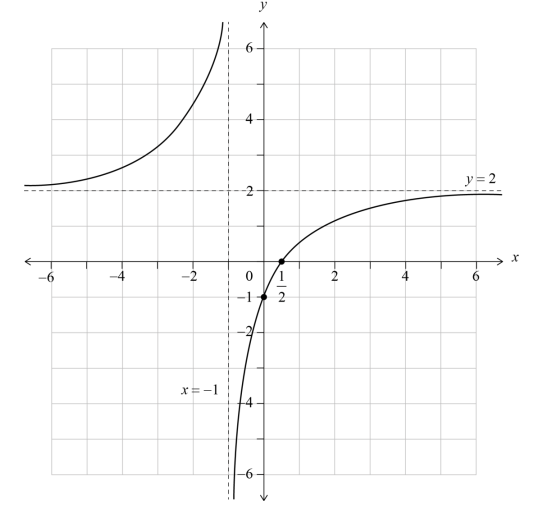 
rational function shape with two branches in opposite quadrants, with two correctly positioned asymptotes and asymptotic behaviour shown axes intercepts clearly shown at \(x = \frac{1}{2} and y = -1\)
(c) x > \(\frac{1}{2}\)
Note: Accept correct alternative correct notation, such as \(\left ( \frac{1}{2}, \infty \right ) and ]\frac{1}{2}, \infty [.\)
(d) EITHER
attempts to sketch \(y = \frac{2|x| – 1}{|x|+1}\)
OR
attempts to solve 2|x| – 1 = 0
Note: Award the (M1) if \(x = \frac{1}{2} and x = -\frac{1}{2}\) are identified.
THEN
\(x <-\frac{1}{2} and x >\frac{1}{2}\)
Note: Accept the use of a comma. Condone the use of ‘and’. Accept correct alternative notation.
Question
The graphs of \(y = \left| {x + 1} \right|\) and \(y = \left| {x – 3} \right|\) are shown below.
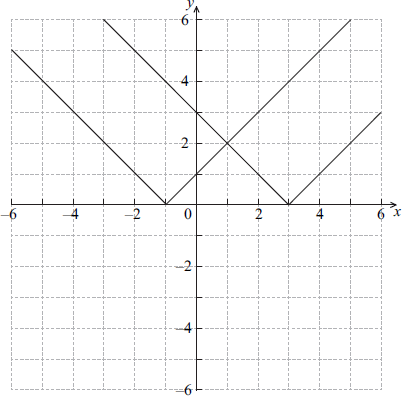
Let f (x) = \(\left| {\,x + 1\,} \right| – \left| {\,x – 3\,} \right|\).
Draw the graph of y = f (x) on the blank grid below.
[4]
Hence state the value of
(i) \(f'( – 3)\);
(ii) \(f'(2.7)\);
(iii) \(\int_{ – 3}^{ – 2} {f(x)dx} \).[4]
▶️Answer/Explanation
Markscheme
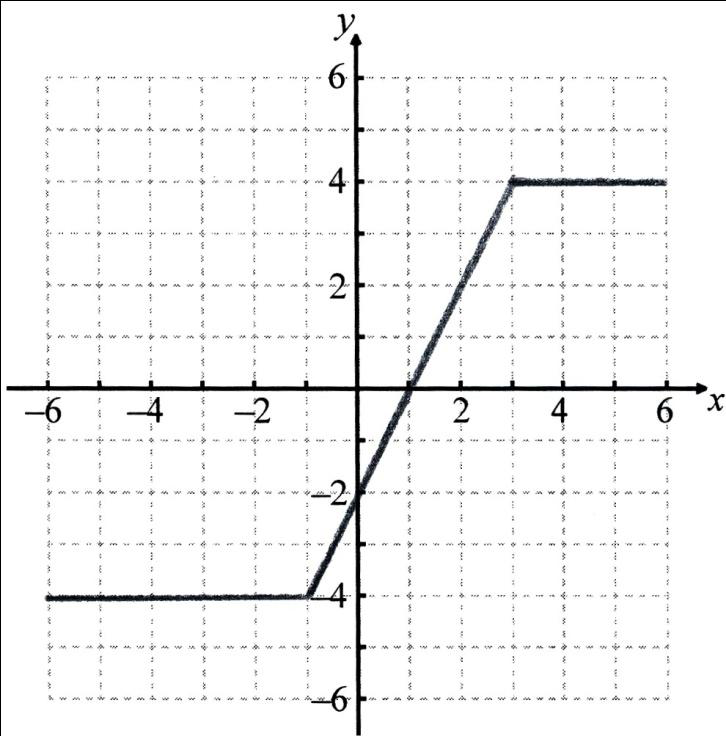M1A1A1A1
Note: Award M1 for any of the three sections completely correct, A1 for each correct segment of the graph.
[4 marks]
(i) 0 A1
(ii) 2 A1
(iii) finding area of rectangle (M1)
\( – 4\) A1
Note: Award M1A0 for the answer 4.
[4 marks]
Question
A rational function is defined by \(f(x) = a + \frac{b}{{x – c}}\) where the parameters \(a,{\text{ }}b,{\text{ }}c \in \mathbb{Z}\) and \(x \in \mathbb{R}\backslash \{ c\} \). The following diagram represents the graph of \(y = f(x)\).
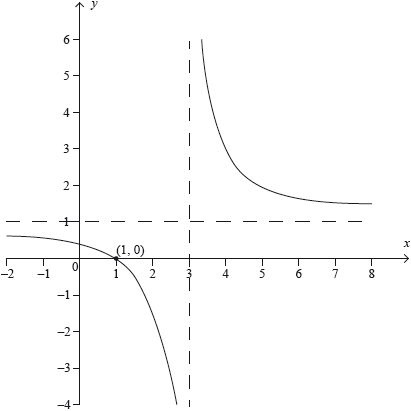
Using the information on the graph,
state the value of \(a\) and the value of \(c\);[2]
find the value of \(b\).[2]
▶️Answer/Explanation
Markscheme
\(a = 1\) A1
\(c = 3\) A1
[2 marks]
use the coordinates of \((1,{\text{ }}0)\) on the graph M1
\(f(1) = 0 \Rightarrow 1 + \frac{b}{{1 – 3}} = 0 \Rightarrow b = 2\) A1
[2 marks]
Question
Sketch the graphs of \(y = \frac{x}{2} + 1\) and \(y = \left| {x – 2} \right|\) on the following axes.
[3]
Solve the equation \(\frac{x}{2} + 1 = \left| {x – 2} \right|\).[4]
▶️Answer/Explanation
Markscheme
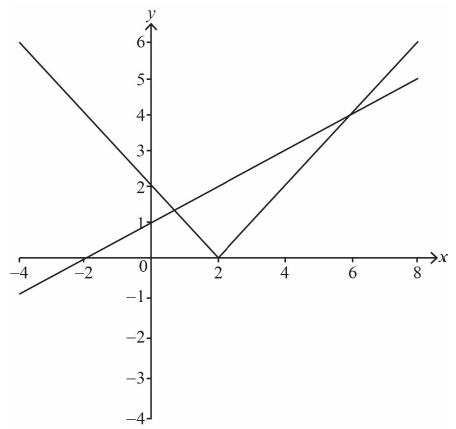
straight line graph with correct axis intercepts A1
modulus graph: V shape in upper half plane A1
modulus graph having correct vertex and y-intercept A1
[3 marks]
METHOD 1
attempt to solve \(\frac{x}{2} + 1 = x – 2\) (M1)
\(x = 6\) A1
Note: Accept \(x = 6\) using the graph.
attempt to solve (algebraically) \(\frac{x}{2} + 1 = 2 – x\) M1
\(x = \frac{2}{3}\) A1
[4 marks]
METHOD 2
\({\left( {\frac{x}{2} + 1} \right)^2} = {\left( {x – 2} \right)^2}\) M1
\(\frac{{{x^2}}}{4} + x + 1 = {x^2} – 4x + 4\)
\(0 = \frac{{3{x^2}}}{4} – 5x + 3\)
\(3{x^2} – 20x + 12 = 0\)
attempt to factorise (or equivalent) M1
\(\left( {3x – 2} \right)\left( {x – 6} \right) = 0\)
\(x = \frac{2}{3}\) A1
\(x = 6\) A1
[4 marks]