Question
The graph below shows \(y = f(x)\) , where \(f(x) = x + \ln x\) .
(a) On the graph below, sketch the curve \(y = {f^{ – 1}}(x)\) .
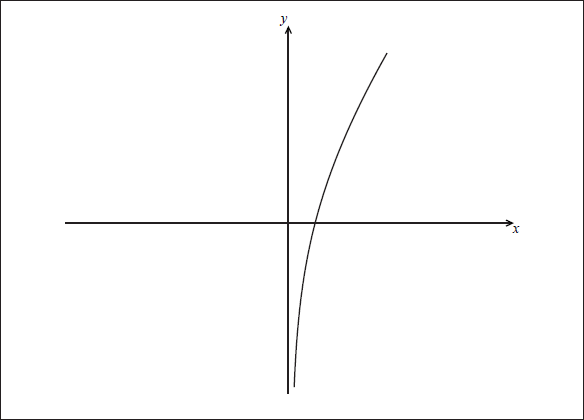
(b) Find the coordinates of the point of intersection of the graph of \(y = f(x)\) and the graph of \(y = {f^{ – 1}}(x)\) .
▶️Answer/Explanation
Markscheme
(a)
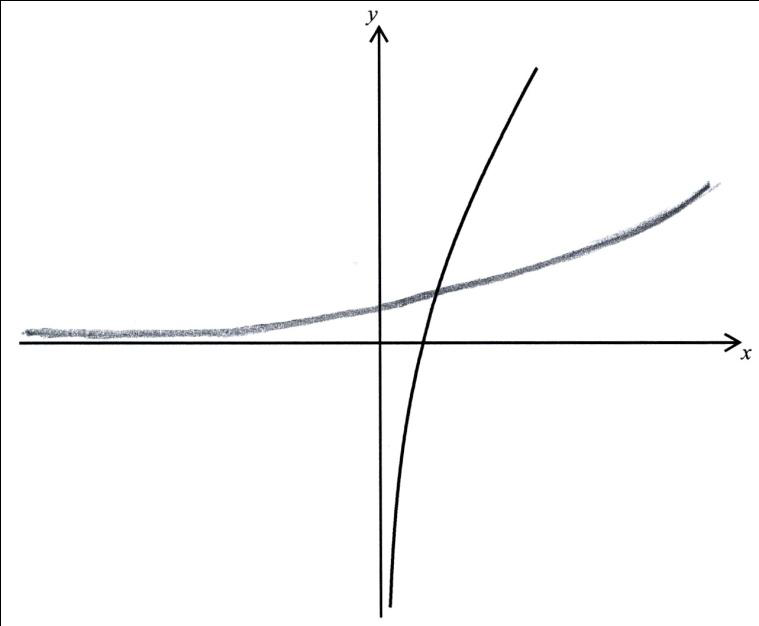A1A1
Note: Award A1 for correct asymptote with correct behaviour and A1 for shape.
[2 marks]
(b) intersect on \(y = x\) (M1)
\(x + \ln x = x \Rightarrow \ln x = 0\) (A1)
intersect at (1, 1) A1 A1
[4 marks]
Total [6 marks]
Question
The function f is defined by \(f(x) = \frac{{2x – 1}}{{x + 2}}\), with domain \(D = \{ x: – 1 \leqslant x \leqslant 8\} \).
a. Express \(f(x)\) in the form \(A + \frac{B}{{x + 2}}\), where \(A\) and \(B \in \mathbb{Z}\).[2]
b. Hence show that \(f'(x) > 0\) on D.[2]
c. State the range of f.[2]
(i) Find an expression for \({f^{ – 1}}(x)\).
(ii) Sketch the graph of \(y = f(x)\), showing the points of intersection with both axes.
(iii) On the same diagram, sketch the graph of \(y = f'(x)\).[8]
(i) On a different diagram, sketch the graph of \(y = f(|x|)\) where \(x \in D\).
(ii) Find all solutions of the equation \(f(|x|) = – \frac{1}{4}\).[7]
▶️Answer/Explanation
Markscheme
a.by division or otherwise
\(f(x) = 2 – \frac{5}{{x + 2}}\) A1A1
[2 marks]
\(f'(x) = \frac{5}{{{{(x + 2)}^2}}}\) A1
> 0 as \({(x + 2)^2} > 0\) (on D) R1AG
Note: Do not penalise candidates who use the original form of the function to compute its derivative.
[2 marks]
\(S = \left[ { – 3,\frac{3}{2}} \right]\) A2
Note: Award A1A0 for the correct endpoints and an open interval.
[2 marks]
(i) EITHER
rearrange \(y = f(x)\) to make x the subject M1
obtain one-line equation, e.g. \(2x – 1 = xy + 2y\) A1
\(x = \frac{{2y + 1}}{{2 – y}}\) A1
OR
interchange x and y M1
obtain one-line equation, e.g. \(2y – 1 = xy + 2x\) A1
\(y = \frac{{2x + 1}}{{2 – x}}\) A1
THEN
\({f^{ – 1}}(x) = \frac{{2x + 1}}{{2 – x}}\) A1
Note: Accept \(\frac{5}{{2 – x}} – 2\)
(ii), (iii)
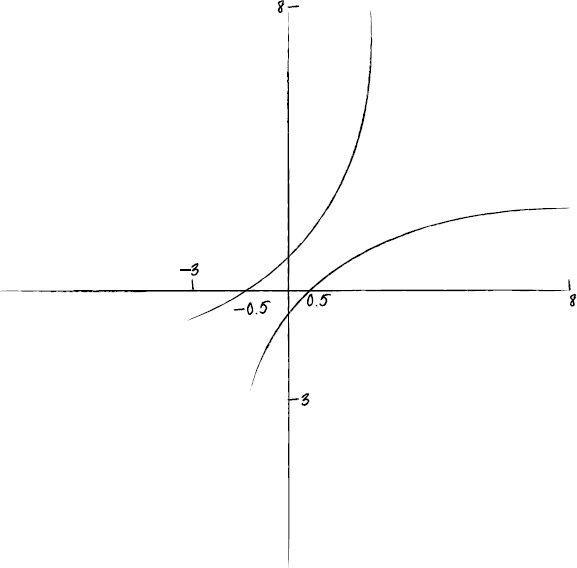A1A1A1A1
[8 marks]
Note: Award A1 for correct shape of \(y = f(x)\).
Award A1 for x intercept \(\frac{1}{2}\) seen. Award A1 for y intercept \( – \frac{1}{2}\) seen.
Award A1 for the graph of \(y = {f^{ – 1}}(x)\) being the reflection of \(y = f(x)\) in the line \(y = x\). Candidates are not required to indicate the full domain, but \(y = f(x)\) should not be shown approaching \(x = – 2\). Candidates, in answering (iii), can FT on their sketch in (ii).
(i)
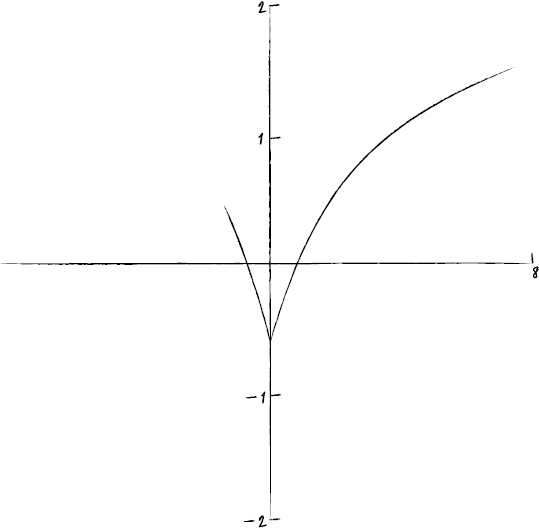A1A1A1
Note: A1 for correct sketch \(x > 0\), A1 for symmetry, A1 for correct domain (from –1 to +8).
Note: Candidates can FT on their sketch in (d)(ii).
(ii) attempt to solve \(f(x) = – \frac{1}{4}\) (M1)
obtain \(x = \frac{2}{9}\) A1
use of symmetry or valid algebraic approach (M1)
obtain \(x = – \frac{2}{9}\) A1
[7 marks]
Question
The diagram below shows a sketch of the graph of \(y = f(x)\).
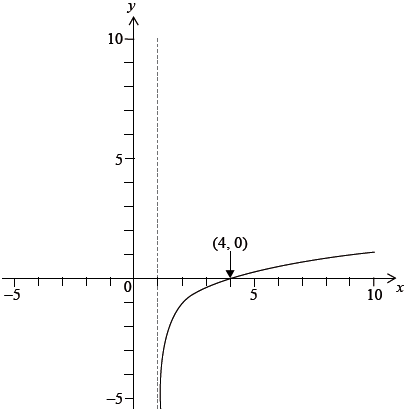
a.Sketch the graph of \(y = {f^{ – 1}}(x)\) on the same axes.[2]
b. State the range of \({f^{ – 1}}\).[1]
c. Given that \(f(x) = \ln (ax + b),{\text{ }}x > 1\), find the value of \(a\) and the value of \(b\).[4]
▶️Answer/Explanation
Markscheme
(a)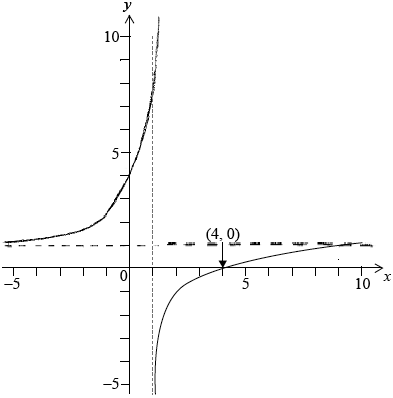 
a.shape with y-axis intercept (0, 4) A1
Note: Accept curve with an asymptote at \(x = 1\) suggested.
correct asymptote \(y = 1\) A1
[2 marks]
range is \({f^{ – 1}}(x) > 1{\text{ (or }}\left] {1,{\text{ }}\infty } \right[)\) A1
Note: Also accept \(\left] {1,{\text{ 10}}} \right]\) or \(\left] {1,{\text{ 10}}} \right[\).
Note: Do not allow follow through from incorrect asymptote in (a).
[1 mark]
\((4,{\text{ }}0) \Rightarrow \ln (4a + b) = 0\) M1
\( \Rightarrow 4a + b = 1\) A1
asymptote at \(x = 1 \Rightarrow a + b = 0\) M1
\( \Rightarrow a = \frac{1}{3},{\text{ }}b = – \frac{1}{3}\) A1
[4 marks]