(a) Minimum Value and Inequality:

(i) To find the minimum value of \( f(x) = e^x – 1 – x \), compute the derivative:
\( f'(x) = e^x – 1 \). Set \( f'(x) = 0 \): \( e^x – 1 = 0 \), so \( e^x = 1 \), thus \( x = 0 \).
Check the second derivative: \( f”(x) = e^x \), and at \( x = 0 \), \( f”(0) = e^0 = 1 > 0 \), indicating a local minimum.
Evaluate \( f(0) = e^0 – 1 – 0 = 1 – 1 = 0 \).
The graph of \( y = f(x) \):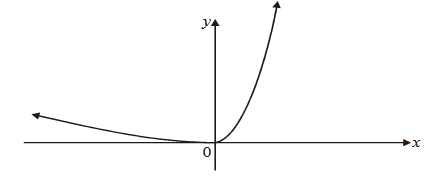

Since \( f”(x) > 0 \) for all \( x \), the function is concave up, and \( x = 0 \) is the global minimum. Thus, the minimum value is \( 0 \).
Answer: \( \boxed{0} \)

(ii) From part (i), \( f(x) = e^x – 1 – x \geq 0 \) for all \( x \), with equality at \( x = 0 \).
Thus, \( e^x – 1 – x \geq 0 \implies e^x \geq 1 + x \).
Answer: \( \boxed{e^x \geq 1 + x} \)

(b) Mathematical Induction:

Let \( P(n) \) be the proposition: \( \left( 1 + 1 \right) \left( 1 + \frac{1}{2} \right) \left( 1 + \frac{1}{3} \right) \dots \left( 1 + \frac{1}{n} \right) = n + 1 \).
Base Case: For \( n = 1 \), \( 1 + 1 = 2 \), and \( n + 1 = 1 + 1 = 2 \). Thus, \( P(1) \) is true.
Inductive Step: Assume \( P(k) \) is true for some integer \( k \geq 1 \), i.e.,
\( \left( 1 + 1 \right) \left( 1 + \frac{1}{2} \right) \left( 1 + \frac{1}{3} \right) \dots \left( 1 + \frac{1}{k} \right) = k + 1 \).
Prove \( P(k + 1) \):
\( \left( 1 + 1 \right) \left( 1 + \frac{1}{2} \right) \left( 1 + \frac{1}{3} \right) \dots \left( 1 + \frac{1}{k} \right) \left( 1 + \frac{1}{k + 1} \right) = (k + 1) \cdot \left( 1 + \frac{1}{k + 1} \right) \).
Simplify: \( (k + 1) \cdot \frac{k + 2}{k + 1} = k + 2 \).
Thus, \( P(k) \implies P(k + 1) \). By the principle of mathematical induction, \( P(n) \) is true for all integers \( n \geq 1 \).
Answer: \( \boxed{\left( 1 + 1 \right) \left( 1 + \frac{1}{2} \right) \left( 1 + \frac{1}{3} \right) \dots \left( 1 + \frac{1}{n} \right) = n + 1} \)

(c) Exponential Inequality:

We need to prove \( e^{1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n}} > n \).
Rewrite the exponent: \( e^{1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n}} = e^1 \cdot e^{\frac{1}{2}} \cdot e^{\frac{1}{3}} \dots e^{\frac{1}{n}} \).
From part (a)(ii), \( e^x \geq 1 + x \), so for each term:
\( e^1 \geq 1 + 1 = 2 \), \( e^{\frac{1}{2}} \geq 1 + \frac{1}{2} \), …, \( e^{\frac{1}{n}} \geq 1 + \frac{1}{n} \).
Thus, \( e^1 \cdot e^{\frac{1}{2}} \cdot e^{\frac{1}{3}} \dots e^{\frac{1}{n}} \geq \left( 1 + 1 \right) \left( 1 + \frac{1}{2} \right) \left( 1 + \frac{1}{3} \right) \dots \left( 1 + \frac{1}{n} \right) \).
From part (b), \( \left( 1 + 1 \right) \left( 1 + \frac{1}{2} \right) \left( 1 + \frac{1}{3} \right) \dots \left( 1 + \frac{1}{n} \right) = n + 1 \).
Hence, \( e^{1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n}} \geq n + 1 > n \).
Answer: \( \boxed{e^{1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n}} > n} \)

(d) Harmonic Sum:

We need \( 1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n} > 100 \).
From part (c), \( e^{1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n}} > n \).
If \( 1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n} > 100 \), then \( e^{1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n}} > e^{100} \).
Since \( e^{100} \approx 2.688 \times 10^{43} \), choose \( n > e^{100} \).
For example, \( n = \lceil e^{100} \rceil \approx 2.689 \times 10^{43} \) ensures the harmonic sum exceeds 100, as \( e^{1 + \frac{1}{2} + \dots + \frac{1}{n}} > n > e^{100} \).
Answer: \( \boxed{n > e^{100}} \)