Question: [Maximum mark: 8]
A function f is defined by f(x) = \(\frac{2x – 1}{x + 1}\), where x ∈ R, x ≠ -1.
(a) The graph of y = f (x) has a vertical asymptote and a horizontal asymptote.
Write down the equation of
(i) the vertical asymptote;
(ii) the horizontal asymptote.
(b) On the set of axes below, sketch the graph of y = f (x) .
On your sketch, clearly indicate the asymptotes and the position of any points of intersection with the axes.
(c) Hence, solve the inequality \(0<\frac{2x – 1}{x + 1} <2.\)
(d) Solve the inequality \(0<\frac{2|x|-1}{|x| + 1} <2.\)
▶️Answer/Explanation
Ans:
(a) (i) x =−1
(ii) y = 2
(b) 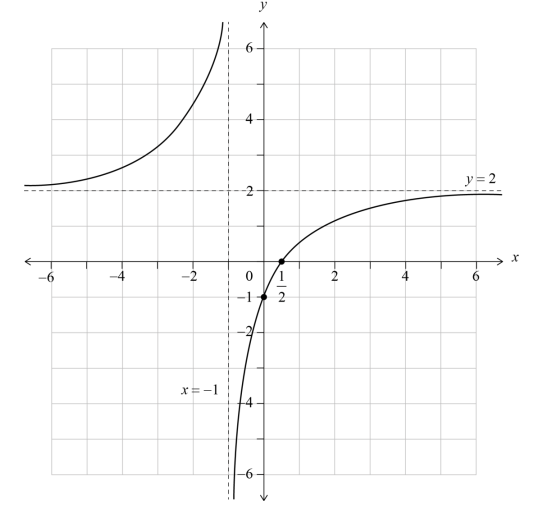
rational function shape with two branches in opposite quadrants, with two correctly positioned asymptotes and asymptotic behaviour shown axes intercepts clearly shown at \(x = \frac{1}{2} and y = -1\)
(c) x > \(\frac{1}{2}\)
Note: Accept correct alternative correct notation, such as \(\left ( \frac{1}{2}, \infty \right ) and ]\frac{1}{2}, \infty [.\)
(d) EITHER
attempts to sketch \(y = \frac{2|x| – 1}{|x|+1}\)
OR
attempts to solve 2|x| – 1 = 0
Note: Award the (M1) if \(x = \frac{1}{2} and x = -\frac{1}{2}\) are identified.
THEN
\(x <-\frac{1}{2} and x >\frac{1}{2}\)
Note: Accept the use of a comma. Condone the use of ‘and’. Accept correct alternative notation.
Question
[Maximum mark: 7]
The function \(f\) is defined by \(f(x)=\frac{7 x+7}{2 x-4}\) for \(x \in \mathbb{R}, x \neq 2\).
(a) Find the zero of \(f(x)\).[2]
(b) For the graph of \(y=f(x)\), write down the equation of
(i) the vertical asymptote;
(ii) the horizontal asymptote.[2]
(c) Find \(f^{-1}(x)\), the inverse function of \(f(x)\).[3]
▶️Answer/Explanation
Ans:
(a) recognizing \(f(x)=0\)
\(f(x)=\frac{7 x+7}{2 x-4}\) =0
$
x=-1
$
(b) (i) \(\quad x=2\) (must be an equation with \(x\) )
x=2.
(ii) \(y=\frac{7}{2}\) (must be an equation with \(y\) )
(c) EITHER
interchanging \(x\) and \(y\)
$
2 x y-4 x=7 y+7
$
correct working with \(\mathrm{y}\) terms on the same side: \(2 x y-7 y=4 x+7\)
OR
$
2 y x-4 y=7 x+7
$
correct working with \(x\) terms on the same side: \(2 y x-7 x=4 y+7\) interchanging \(x\) and \(y\) OR making \(x\) the subject \(x=\frac{4 y+7}{2 y-7}\)
THEN
$
f^{-1}(x)=\frac{4 x+7}{2 x-7} \text { (or equivalent) }\left(x \neq \frac{7}{2}\right)
$
Detailed Explanation:
a) f(x)=0
\(f(x)=\frac{7 x+7}{2 x-4}\) =0
7x+7=0
x=-1.
b) i) For vertical asymptote, set the denominator equal to zero and solve for x.
2x-4=0
x=2.
b) ii) For horizontal asymptote,
Degree of numerator, N =1, Degree of denominator, D =1,
Here, N=D so,
The equation of horizontal asymptote is y= ratio of leading coefficients i.e. \(y=\frac{7}{2}\)
c) To get \(f^{-1}(x)\) ,
interchange x and y,
i.e. 2 x y-4 x=7 y+7
2 x y-7 y=4 x+7
y= \(\frac{4 x+7}{2 x-7} \)
$
f^{-1}(x)=\frac{4 x+7}{2 x-7} \text { (or equivalent) }\left(x \neq \frac{7}{2}\right)
$
Question
Consider the function defined by f ( x ) = \(\frac{kx-5}{x-k}\), where x ∈ \(\mathbb{R}\) \ {k} and k2 ≠5 .
State the equation of the vertical asymptote on the graph of y = f ( x ) . [1]
State the equation of the horizontal asymptote on the graph of y = f ( x ) . [1]
Use an algebraic method to determine whether f is a self-inverse function. [4] Consider the case where k = 3 .
Sketch the graph of y = f ( x ) , stating clearly the equations of any asymptotes and the coordinates of any points of intersections with the coordinate axes. [3]
The region bounded by the x-axis, the curve y = f ( x ) , and the lines x = 5 and x = 7 is rotated through 2π about the x-axis. Find the volume of the solid generated, giving your answer in the form π ( a + b ln 2 ) , where a , b ∈ \(\mathbb{Z}\). [6]
▶️Answer/Explanation
Ans:
(a) x = k
(b) y = k
(c)
METHOD 1
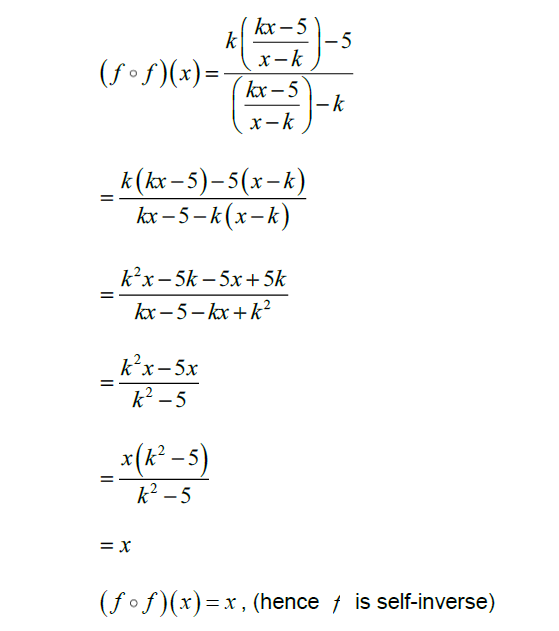
METHOD 2

(d)
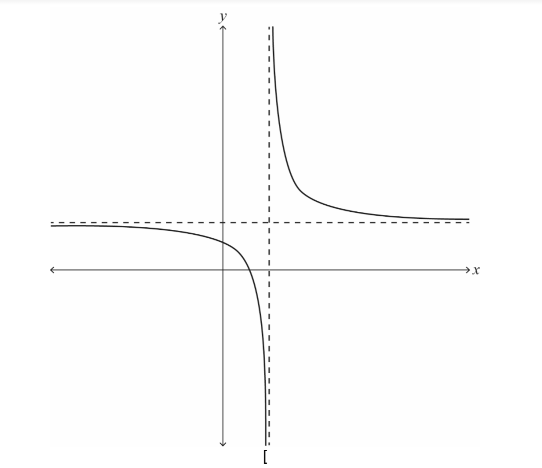
attempt to draw both branches of a rectangular hyperbola x=3 and y=3
(0,\(\frac{5}{3})and (\frac{5}{3}\),0)
(e)
METHOD 1
volume = \(\pi \int_{5}^{7}(\frac{3x-5}{x-3})^{2}\)dx
EITHER
attempt to express \(\frac{3x-5}{x-3} \)in the form \(p+ \frac{q}{x-3}\)
\(\frac{3x-5}{x-3}=3+\frac{4}{x-3}\)
OR attempt to expand
\((\frac{3x-5}{x-3})^{2}or (3x-5)^{2}\)and divide out
\((\frac{3x-5}{x-3})^{2} = 9+ \frac{24x-56}{(x-3)^{2}}\)
THEN
\((\frac{3x-5}{x-3})^{2}= 9+\frac{24}{x-3}+\frac{16}{(x-3)^{2}}\)
volume = \(\pi \int_{5}^{7}(9+\frac{24}{x-3}+\frac{16}{(x-3)^{2}})\)dx = \(\pi [9x+24ln(x-3)-\frac{16}{x-3}]^{7}_{5} =π [(63+ 24ln 4 − 4) − (45 + 24ln 2 −8)]=\pi (22+24ln2)\)
