a. Solutions of \( f(x) > 0 \):

Let \( f(x) = x^4 + 0.2x^3 – 5.8x^2 – x + 4 \). To find where \( f(x) > 0 \), solve \( f(x) = 0 \).
Using numerical methods or graphing (e.g., a calculator or software), find the roots of the quartic equation.
Approximate roots are \( x \approx -2.24 \), \( x \approx -1 \), \( x \approx 0.8 \), \( x \approx 2.24 \).
Test intervals: \( (-\infty, -2.24) \), \( (-2.24, -1) \), \( (-1, 0.8) \), \( (0.8, 2.24) \), \( (2.24, \infty) \).
Using test points or the graph, \( f(x) > 0 \) for \( x < -2.24 \), \( -1 < x < 0.8 \), and \( x > 2.24 \).
Note: Award M1 for a valid method (e.g., sketching the curve or finding critical values). Award M1A1A0 if correct intervals are given but with inclusive inequalities.
Answer: \( \boxed{x < -2.24, \, -1 < x < 0.8, \, x > 2.24} \)

b. Local Minima and Points of Inflection:

(i) Local Minima: Compute the derivative: \( f'(x) = 4x^3 + 0.6x^2 – 11.6x – 1 \).
Set \( f'(x) = 0 \). Solve numerically: roots at \( x \approx -1.74 \), \( x \approx 1.67 \).
Second derivative: \( f”(x) = 12x^2 + 1.2x – 11.6 \). At \( x = -1.74 \), \( f”(-1.74) > 0 \); at \( x = 1.67 \), \( f”(1.67) > 0 \), confirming minima.
Evaluate \( f(x) \): \( f(-1.74) \approx -3.71 \), \( f(1.67) \approx -5.14 \).
Note: Award A1A0 for any two correct terms (x or y coordinates).
Answer: \( \boxed{(1.67, -5.14), (-1.74, -3.71)} \)

(ii) Points of Inflection: Set \( f”(x) = 12x^2 + 1.2x – 11.6 = 0 \).
Solve: \( x = \frac{-1.2 \pm \sqrt{1.2^2 + 4 \cdot 12 \cdot 11.6}}{24} \approx -1.03, 0.934 \).
Note: Award M1 for graphical method or solving \( f”(x) = 0 \).
Answer: \( \boxed{x = -1.03, 0.934} \)

c. Inverse Function:

(i) Largest \( a \): For \( f \) to have an inverse on \( [0, a] \), it must be one-to-one. Since \( f'(x) = 0 \) at \( x \approx 1.67 \), and \( f'(x) > 0 \) for \( x > 1.67 \), \( f \) is increasing on \( [1.67, a] \). The largest \( a \) is at the local maximum, \( x \approx 1.67 \).
Answer: \( \boxed{1.67} \)

(ii) Sketch Graphs: For \( a = 1.67 \), \( f: [0, 1.67] \to [4, -5.14] \). End points of \( y = f(x) \): \( (0, 4) \), \( (1.67, -5.14) \).
For \( y = f^{-1}(x) \), reflect over \( y = x \): end points \( (4, 0) \), \( (-5.14, 1.67) \).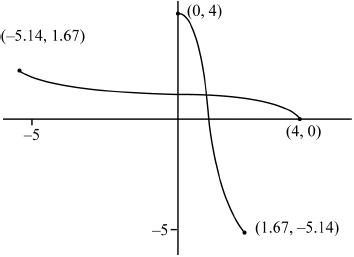

Note: Award M1 for reflection of \( y = f(x) \) in \( y = x \) if \( f \) is one-to-one. Award A1 for \( (0, 4) \), \( (4, 0) \), and A1 for other end points.
Answer: Graph with end points \( (0, 4) \), \( (1.67, -5.14) \) for \( f \), and \( (4, 0) \), \( (-5.14, 1.67) \) for \( f^{-1} \).

(iii) Solve \( f^{-1}(x) = 1 \): If \( f^{-1}(x) = 1 \), then \( x = f(1) \).
Compute: \( f(1) = 1^4 + 0.2 \cdot 1^3 – 5.8 \cdot 1^2 – 1 + 4 = 1 + 0.2 – 5.8 – 1 + 4 = -1.6 \).
Answer: \( \boxed{-1.6} \)

d. Inverse of \( g \) and Composition:

(i) Inverse of \( g \): Let \( y = g(x) = 2 \sin (x – 1) – 3 \). Solve for \( x \):
\( y = 2 \sin (x – 1) – 3 \implies y + 3 = 2 \sin (x – 1) \implies \sin (x – 1) = \frac{y + 3}{2} \).
\( x – 1 = \arcsin \left( \frac{y + 3}{2} \right) \implies x = \arcsin \left( \frac{y + 3}{2} \right) + 1 \).
Thus, \( g^{-1}(x) = \arcsin \left( \frac{x + 3}{2} \right) + 1 \).
Domain of \( g^{-1} \): Since \( g(x) = 2 \sin (x – 1) – 3 \), range of \( g \): \( \sin (x – 1) \in [-1, 1] \), so \( 2 \sin (x – 1) \in [-2, 2] \), and \( g(x) \in [-5, -1] \). Thus, domain of \( g^{-1} \) is \( [-5, -1] \).
Answer: \( \boxed{g^{-1}(x) = \arcsin \left( \frac{x + 3}{2} \right) + 1, \, -5 \leqslant x \leqslant -1} \)

(ii) Solve \( (f^{-1} \circ g)(x) < 1 \): This means \( f^{-1}(g(x)) < 1 \). From part c(iii), \( f^{-1}(-1.6) = 1 \), so we need \( g(x) < -1.6 \).
Solve: \( 2 \sin (x – 1) – 3 < -1.6 \implies 2 \sin (x – 1) < 1.4 \implies \sin (x – 1) < 0.7 \).
Since \( \arcsin(0.7) \approx 0.775 \), and \( \sin (x – 1) \) is increasing, \( x – 1 < 0.775 \implies x < 1.775 \).
Domain of \( g \): \( x \in \left[ -\frac{\pi}{2} + 1, \frac{\pi}{2} + 1 \right] \approx [-0.571, 2.571] \). Thus, solution is \( x < 1.775 \), and within domain, \( -\frac{\pi}{2} + 1 \leq x < 1.775 \).
Compute \( g^{-1}(-1.6) \): \( g^{-1}(-1.6) = \arcsin \left( \frac{-1.6 + 3}{2} \right) + 1 = \arcsin(0.7) + 1 \approx 0.775 + 1 = 1.775 \).
Note: Award M1 for setting \( g(x) > -1.6 \). Award A1 for \( x > 1.78 \), and A1 for \( x \leq \frac{\pi}{2} + 1 \). Accept equality in inequalities.
Answer: \( \boxed{1.78 < x \leqslant \frac{\pi}{2} + 1} \)