Question
Find the values of \(k\) such that the equation \({x^3} + {x^2} – x + 2 = k\) has three distinct real solutions.
▶️Answer/Explanation
Markscheme
from GDC, sketch a relevant graph A1
maximum: \(y = 3\) or (–1, 3) A1
minimum: \(y = 1.81\) or (0.333, 1.81) \(\left( {{\text{or }}y = \frac{{49}}{{27}}{\text{ or }}\left( {\frac{1}{3},\frac{{49}}{{27}}} \right)} \right)\) A1
hence, \(1.81 < k < 3\) A1A1 N3
Note: Award A1 for \(1.81 \leqslant k \leqslant 3\) .
[5 marks]
Examiners report
Responses to this question were surprisingly poor. Few candidates recognised that the easier way to answer the question was to use a graph on the GDC. Many candidates embarked on fruitless algebraic manipulation which led nowhere.
Question
The function f is defined by
\[f(x) = {({x^3} + 6{x^2} + 3x – 10)^{\frac{1}{2}}},{\text{ for }}x \in D,\]
where \(D \subseteq \mathbb{R}\) is the greatest possible domain of f.
(a) Find the roots of \(f(x) = 0\).
(b) Hence specify the set D.
(c) Find the coordinates of the local maximum on the graph \(y = f(x)\).
(d) Solve the equation \(f(x) = 3\).
(e) Sketch the graph of \(\left| y \right| = f(x),{\text{ for }}x \in D\).
(f) Find the area of the region completely enclosed by the graph of \(\left| y \right| = f(x)\)
▶️Answer/Explanation
Markscheme
(a) solving to obtain one root: 1, – 2 or – 5 A1
obtain other roots A1
[2 marks]
(b) \(D = x \in [ – 5,{\text{ }} – 2] \cup [1,{\text{ }}\infty {\text{)}}\) (or equivalent) M1A1
Note: M1 is for 1 finite and 1 infinite interval.
[2 marks]
(c) coordinates of local maximum \( – 3.73 – 2 – \sqrt 3 ,{\text{ }}3.22\sqrt {6\sqrt 3 } \) A1A1
[2 marks]
(d) use GDC to obtain one root: 1.41, – 3.18 or – 4.23 A1
obtain other roots A1
[2 marks]
(e)
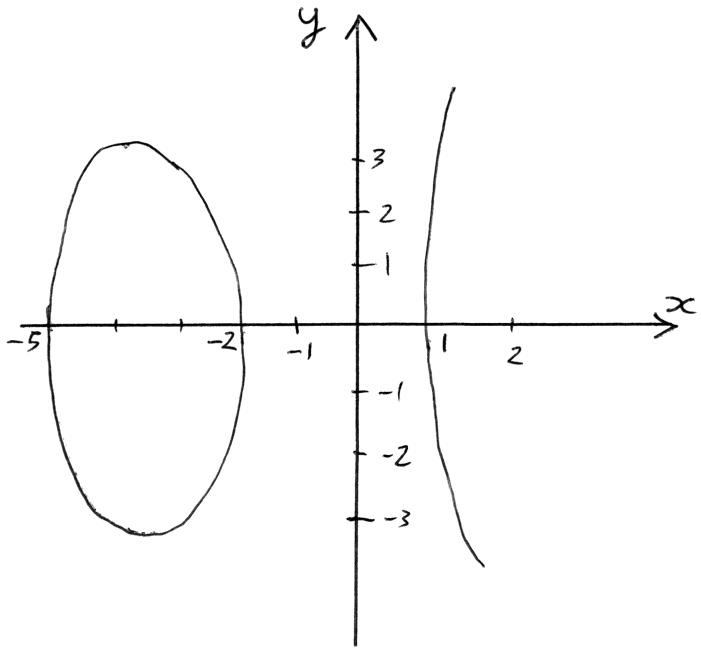A1A1A1
Note: Award A1 for shape, A1 for max and for min clearly in correct places, A1 for all intercepts.
Award A1A0A0 if only the complete top half is shown.
[3 marks]
(f) required area is twice that of \(y = f(x)\) between – 5 and – 2 M1A1
answer 14.9 A1 N3
Note: Award M1A0A0 for \(\int_{ – 5}^{ – 2} {f(x){\text{d}}x = 7.47 \ldots } \) or N1 for 7.47.
[3 marks]
Total [14 marks]
Examiners report
This was a multi-part question that was well answered by many candidates. The main difficulty was sketching the graph and this meant that the last part was not well answered.
Question
The vectors a and b are such that a \( = (3\cos \theta + 6)\)i \( + 7\) j and b \( = (\cos \theta – 2)\)i \( + (1 + \sin \theta )\)j.
Given that a and b are perpendicular,
a.show that \(3{\sin ^2}\theta – 7\sin \theta + 2 = 0\);[3]
b.find the smallest possible positive value of \(\theta \).[3]
▶️Answer/Explanation
Markscheme
attempting to form \((3\cos \theta + 6)(\cos \theta – 2) + 7(1 + \sin \theta ) = 0\) M1
\(3{\cos ^2}\theta – 12 + 7\sin \theta + 7 = 0\) A1
\(3\left( {1 – {{\sin }^2}\theta } \right) + 7\sin \theta – 5 = 0\) M1
\(3{\sin ^2}\theta – 7\sin \theta + 2 = 0\) AG
[3 marks]
attempting to solve algebraically (including substitution) or graphically for \(\sin \theta \) (M1)
\(\sin \theta = \frac{1}{3}\) (A1)
\(\theta = 0.340{\text{ }}( = 19.5^\circ )\) A1
[3 marks]
Examiners report
Part (a) was very well done. Most candidates were able to use the scalar product and \({\cos ^2}\theta = 1 – {\sin ^2}\theta \) to show the required result.
Part (b) was reasonably well done. A few candidates confused ‘smallest possible positive value’ with a minimum function value. Some candidates gave \(\theta = 0.34\) as their final answer.
Question
Let \(f(x) = {x^4} + 0.2{x^3} – 5.8{x^2} – x + 4,{\text{ }}x \in \mathbb{R}\).
The domain of \(f\) is now restricted to \([0,{\text{ }}a]\).
Let \(g(x) = 2\sin (x – 1) – 3,{\text{ }} – \frac{\pi }{2} + 1 \leqslant x \leqslant \frac{\pi }{2} + 1\).
a.Find the solutions of \(f(x) > 0\).[3]
b.For the curve \(y = f(x)\).
(i) Find the coordinates of both local minimum points.
(ii) Find the \(x\)-coordinates of the points of inflexion.[5]
c.i.Write down the largest value of \(a\) for which \(f\) has an inverse. Give your answer correct to 3 significant figures.[2]
c.ii.For this value of a sketch the graphs of \(y = f(x)\) and \(y = {f^{ – 1}}(x)\) on the same set of axes, showing clearly the coordinates of the end points of each curve.[2]
c.iii.Solve \({f^{ – 1}}(x) = 1\).[2]
d.i.Find an expression for \({g^{ – 1}}(x)\), stating the domain.[4]
d.ii.Solve \(({f^{ – 1}} \circ g)(x) < 1\).[4]
▶️Answer/Explanation
Markscheme
valid method eg, sketch of curve or critical values found (M1)
\(x < – 2.24,{\text{ }}x > 2.24,\) A1
\( – 1 < x < 0.8\) A1
Note: Award M1A1A0 for correct intervals but with inclusive inequalities.
[3 marks]
(i) \((1.67,{\text{ }} – 5.14),{\text{ }}( – 1.74,{\text{ }} – 3.71)\) A1A1
Note: Award A1A0 for any two correct terms.
(ii) \(f'(x) = 4{x^3} + 0.6{x^2} – 11.6x – 1\)
\(f”(x) = 12{x^2} + 1.2x – 11.6 = 0\) (M1)
\( – 1.03,{\text{ }}0.934\) A1A1
Note: M1 should be awarded if graphical method to find zeros of \(f”(x)\) or turning points of \(f'(x)\) is shown.
[5 marks]
1.67 A1
[2 marks]
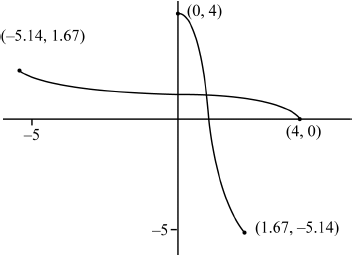M1A1A1
Note: Award M1 for reflection of their \(y = f(x)\) in the line \(y = x\) provided their \(f\) is one-one.
A1 for \((0,{\text{ }}4)\), \((4,{\text{ }}0)\) (Accept axis intercept values) A1 for the other two sets of coordinates of other end points
[2 marks]
\(x = f(1)\) M1
\( = – 1.6\) A1
[2 marks]
\(y = 2\sin (x – 1) – 3\)
\(x = 2\sin (y – 1) – 3\) (M1)
\(\left( {{g^{ – 1}}(x) = } \right){\text{ }}\arcsin \left( {\frac{{x + 3}}{2}} \right) + 1\) A1
\( – 5 \leqslant x \leqslant – 1\) A1A1
Note: Award A1 for −5 and −1, and A1 for correct inequalities if numbers are reasonable.
[8 marks]
\({f^{ – 1}}\left( {g(x)} \right) < 1\)
\(g(x) > – 1.6\) (M1)
\(x > {g^{ – 1}}( – 1.6) = 1.78\) (A1)
Note: Accept = in the above.
\(1.78 < x \leqslant \frac{\pi }{2} + 1\) A1A1
Note: A1 for \(x > 1.78\) (allow ≥) and A1 for \(x \leqslant \frac{\pi }{2} + 1\).
[4 marks]