Question: [Maximum mark: 4]
Consider the equation kx2 – (k + 3) x + 2k + 9 = 0, where k ∈ R.
(a) Write down an expression for the product of the roots, in terms of k .
(b) Hence or otherwise, determine the values of k such that the equation has one positive and one negative real root.
▶️Answer/Explanation
Ans:
(a) product of roots \(=\frac{2k+9}{k}\)
(b) recognition that the product of the roots will be negative
\(=\frac{2k+9}{k}\) < 0
critical values \(k = 0, -\frac{9}{2}\)
\(-\frac{9}{2}<k<0\)
Question
Consider the equation ax2 = bx + c + 0 , where a ≠ 0 . Given that the roots of this equation
are x = sinθ and x = cosθ , show that b2 = a2 + 2ac . [Maximum mark: 4]
▶️Answer/Explanation
Ans:
METHOD 1
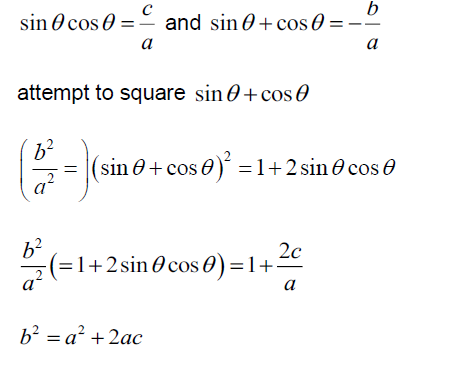
METHOD 2
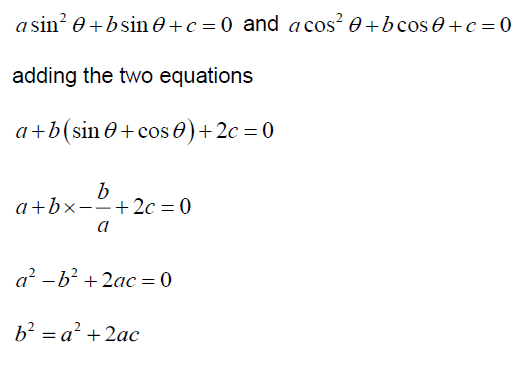
Question
Consider the equation \(y{x^2} + (y – 1)x + (y – 1) = 0\).
Find the set of values of y for which this equation has real roots.[4]
Hence determine the range of the function \(f:x \to \frac{{x + 1}}{{{x^2} + x + 1}}\).[3]
Explain why f has no inverse.[1]
▶️Answer/Explanation
Markscheme
for the equation to have real roots
\({(y – 1)^2} – 4y(y – 1) \geqslant 0\) M1
\( \Rightarrow 3{y^2} – 2y – 1 \leqslant 0\)
(by sign diagram, or algebraic method) M1
\( – \frac{1}{3} \leqslant y \leqslant 1\) A1A1
Note: Award first A1 for \( – \frac{1}{3}\) and 1, and second A1 for inequalities. These are independent marks.
[4 marks]
\(f:x \to \frac{{x + 1}}{{{x^2} + x + 1}} \Rightarrow x + 1 = y{x^2} + yx + y\) (M1)
\( \Rightarrow 0 = y{x^2} + (y – 1)x + (y – 1)\) A1
hence, from (a) range is \( – \frac{1}{3} \leqslant y \leqslant 1\) A1
[3 marks]
a value for y would lead to 2 values for x from (a) R1
Note: Do not award R1 if (b) has not been tackled.
[1 mark]
Question
Consider the graph G of the function f (x) = x2 and the point M(5,2) on the Cartesian plane (a)Find the coordinates of a point A on G and a point B on x-axis, given that M(5,2) is the midpoint of the line segment [AB] (b) Find the coordinates of a point C on G, given that the distance between M and C is 23.
▶️Answer/Explanation
Ans
Let A(a,a2) and B(b,0) be the points on the graph and on x-axis respectively. Then \(\frac{a+b}{2}=5\) and \(\frac{a^2+0}{2}=2\), hence a = ±2 and a = 8 or 12 respectively. Therefore, A(2,4), B(8,0) or A(-1,4), B(12,0) (b) Let C(c,c2) be on the graph. (c-5)2 + (c2 – 2(2 = 232 \(\Leftrightarrow \) c = 5 or c = -4.78 Therefore C(5,25) or C(-4.78,22.8)
Question
The equation kx2–3x+(k + 2) = 0 has two distinct real roots. Find the set of possible values of k.
▶️Answer/Explanation
Ans
For kx2 – 3x + (k + 2) = 0 to have two distinct real roots then k≠ 0 and 9 – 4k(k + 2) > 0 \(4k^2+8k-9< 0\), hence \(-2.803< k< 0.803\) Set of values of k is -2.80 < k < 0.803, k ≠ 0
Question
The function f is defined by f(x)=x2-2x+k(3k+2) where k ∈ \(\mathbb{R}\). Find the set of values of k for which f(x) = 0 has two distinct real roots.
▶️Answer/Explanation
Ans
METHOD 1 \(\Delta =4-4k(3k+2) (=-12k^2-8k+4, = -4(k+1)(3k-1))\) \(\Delta =0\Rightarrow k=-1, k=\frac{1}{3}\) For 2 distinct roots, \(\Delta > 0\) \(-1< k< \frac{1}{3}\) METHOD 2 For 2 distinct roots, Δ>0 \(\Delta =4-4k(3k+2) (=-12k^2-8k+4,–4(k+1)(3k-1))\) \(\Delta =0\Rightarrow k=-1, k=\frac{1}{3}\) \(-1< k< \frac{1}{3}\)
