Question: [Maximum mark: 6]
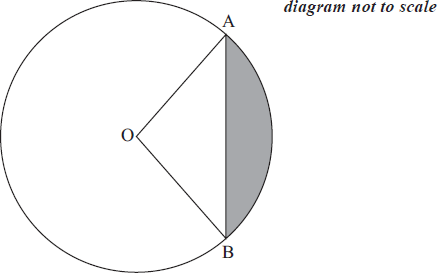
The following diagram shows a circle with centre O and radius 5 metres.
Points A and B lie on the circle and \(A\hat{O}B\) = 1.9 radians.
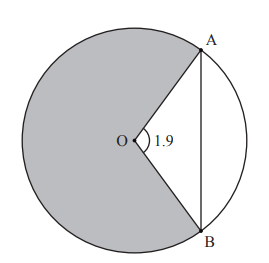
(a) Find the length of the chord [AB].
(b) Find the area of the shaded sector.
▶️Answer/Explanation
Ans:
(a) EITHER
uses the cosine rule
AB2 = 52 + 52 -2 × 5 × 5 × cos1.9
OR
uses right-angled trigonometry
\(\frac{\frac{AB}{2}}{5}= sin 0.95\)
OR
uses the sine rule
\(\alpha \frac{1}{2}(\pi -1.9)(=0.6207…)\)
\(\frac{AB}{sin1.9}= \frac{5}{sin0.6207….}\)
THEN
AB = 8.1341…
AB = 8.13 (m)
(b) let the shaded area be A
METHOD 1
Attempt at finding reflex angle
\(A\hat{O}B = 2\pi -1.9 (=4.3831….)\)
substitution into area formula
\(A = \frac{1}{2}\times 5^{2}\times 4.3831…. OR \left ( \frac{2\pi -1.9}{2\pi } \right )\times \pi \left ( 5^{2} \right )\)
= 54.7898…
= 54.8 (m2)
METHOD 2
let the area of the circle be AC and the area of the unshaded sector be AU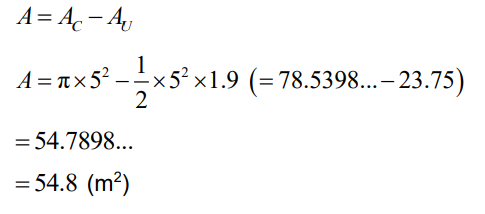
Question
The interior of a circle of radius 2 cm is divided into an infinite number of sectors. The areas of these sectors form a geometric sequence with common ratio k. The angle of the first sector is \(\theta \) radians.
(a) Show that \(\theta = 2\pi (1 – k)\).
(b) The perimeter of the third sector is half the perimeter of the first sector.
Find the value of k and of \(\theta \).
▶️Answer/Explanation
Markscheme
(a) the area of the first sector is \(\frac{1}{2}{2^2}\theta \) (A1)
the sequence of areas is \(2\theta ,{\text{ }}2k\theta ,{\text{ }}2{k^2}\theta \ldots \) (A1)
the sum of these areas is \(2\theta (1 + k + {k^2} + \ldots )\) (M1)
\( = \frac{{2\theta }}{{1 – k}} = 4\pi \) M1A1
hence \(\theta = 2\pi (1 – k)\) AG
Note: Accept solutions where candidates deal with angles instead of area.
[5 marks]
(b) the perimeter of the first sector is \(4 + 2\theta \) (A1)
the perimeter of the third sector is \(4 + 2{k^2}\theta \) (A1)
the given condition is \(4 + 2{k^2}\theta = 2 + \theta \) M1
which simplifies to \(2 = \theta (1 – 2{k^2})\) A1
eliminating \(\theta \), obtain cubic in k: \(\pi (1 – k)(1 – 2{k^2}) – 1 = 0\) A1
or equivalent
solve for k = 0.456 and then \(\theta = 3.42\) A1A1
[7 marks]
Total [12 marks]
Examiners report
This was a disappointingly answered question.
Part(a) – Many candidates correctly assumed that the areas of the sectors were proportional to their angles, but did not actually state that fact.
Part(b) – Few candidates seem to know what the term ‘perimeter’ means.
Question
The radius of the circle with centre C is 7 cm and the radius of the circle with centre D is 5 cm. If the length of the chord [AB] is 9 cm, find the area of the shaded region enclosed by the two arcs AB.
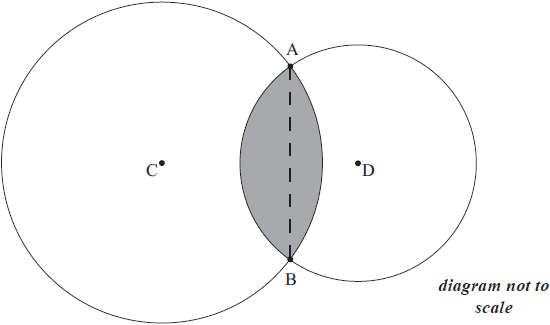
▶️Answer/Explanation
Markscheme

\(\alpha = 2\arcsin \left( {\frac{{4.5}}{7}} \right)\) (\( \Rightarrow \alpha = 1.396… = 80.010^\circ …\)) M1(A1)
\(\beta = 2\arcsin \left( {\frac{{4.5}}{5}} \right)\) (\( \Rightarrow \beta = 2.239… = 128.31^\circ …\)) (A1)
Note: Allow use of cosine rule.
area \(P = \frac{1}{2} \times {7^2} \times \left( {\alpha – \sin \alpha } \right) = 10.08…\) M1(A1)
area \(Q = \frac{1}{2} \times {5^2} \times \left( {\beta – \sin \beta } \right) = 18.18…\) (A1)
Note: The M1 is for an attempt at area of sector minus area of triangle.
Note: The use of degrees correctly converted is acceptable.
area = 28.3 (cm2) A1
[7 marks]
Examiners report
Whilst most candidates were able to make the correct construction to solve the problem some candidates seemed unable to find the area of a segment. In a number of cases candidates used degrees in a formula that required radians. There were a number of candidates who followed a completely correct method but due to premature approximation were unable to obtain a correct solution.
Question
A rectangle is drawn around a sector of a circle as shown. If the angle of the sector is 1 radian and the area of the sector is \(7{\text{ c}}{{\text{m}}^2}\), find the dimensions of the rectangle, giving your answers to the nearest millimetre.
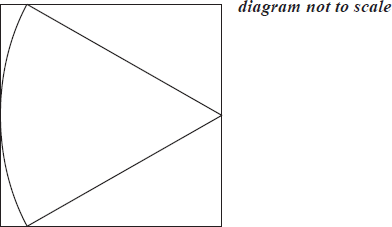
▶️Answer/Explanation
Markscheme
\(\frac{1}{2}{r^2} \times 1 = 7\) M1
\(r = 3.7 \ldots \left( { = \sqrt {14} } \right)\) (or 37… mm) (A1)
\({\text{height}} = 2r\cos \left( {\frac{{\pi – 1}}{2}} \right){\text{ }}\left( {{\text{or }}2r\sin \frac{1}{2}} \right)\) (M1)(A1)
3.59 or anything that rounds to 3.6 A1
so the dimensions are 3.7 by 3.6 (cm or 37 by 36 mm) A1
[6 marks]
Examiners report
Most students found the value of \(r\) , but a surprising number had difficulties finding the height of the rectangle by any one of the many methods possible. Those that did, frequently failed to round their final answer to the required accuracy leading to few students obtaining full marks on this question. A surprising number of students found the area – clearly misinterpreting the meaning of “dimensions”.
Question
A circle of radius 4 cm , centre O , is cut by a chord [AB] of length 6 cm.
a.Find \({\rm{A\hat OB}}\), expressing your answer in radians correct to four significant figures.[2]
b.Determine the area of the shaded region.[3]
▶️Answer/Explanation
Markscheme
EITHER
\({\rm{A\hat OB}} = 2\arcsin \left( {\frac{3}{4}} \right)\) or equivalent (eg \({\rm{A\hat OB}} = 2\arctan \left( {\frac{3}{{\sqrt 7 }}} \right),{\rm{ A\hat OB}} = 2\arccos \left( {\frac{{\sqrt 7 }}{4}} \right)\)) (M1)
OR
\(\cos {\rm{A\hat OB}} = \frac{{{4^2} + {4^2} – {6^2}}}{{2 \times 4 \times 4}}{\text{ }}\left( { = – \frac{1}{8}} \right)\) (M1)
THEN
\( = 1.696\) (correct to 4sf) A1
[2 marks]
use of area of segment = area of sector – area of triangle (M1)
\( = \frac{1}{2} \times {4^2} \times 1.696 – \frac{1}{2} \times {4^2} \times \sin 1.696\) (A1)
\( = 5.63{\text{ (c}}{{\text{m}}^2})\) A1
[3 marks]
Examiners report
This was generally well done. In part (a), a number of candidates expressed the required angle either in degrees or in radians stated to an incorrect number of significant figures.
This was generally well done. In part (b), some candidates demonstrated a correct method to calculate the shaded area using an incorrect formula for the area of a sector.
