Home / IBDP Maths AHL 3.10 Compound angle identities AA HL Paper 1- Exam Style Questions

IBDP Maths AHL 3.10 Compound angle identities AA HL Paper 1- Exam Style Questions- New Syllabus

IB DP Maths AA HL Papers All Topics

Question

The plane \( \Pi_1 \) is defined by the equation \( x + 2y + z = 0 \) and the plane \( \Pi_2 \) is defined by \( x – y – 2z = 0 \). Let \( \theta \) be the acute angle between \( \Pi_1 \) and \( \Pi_2 \).
(a) Show that \( \theta = 60^\circ \).
A third plane, \( \Pi_3 \), is perpendicular to both \( \Pi_1 \) and \( \Pi_2 \). The three planes have a unique point of intersection at \( R(5, -5, 5) \).
(b) Find the Cartesian equation of \( \Pi_3 \).
Reflecting surfaces are located on planes \( \Pi_1 \) and \( \Pi_2 \). A ray of light is directed toward the mirror on \( \Pi_1 \), meeting it at point \( P \) and forming an angle of \( 45^\circ \) with the plane. The ray is reflected toward the mirror on \( \Pi_2 \), where it meets the plane at point \( Q \). Points \( P \) and \( Q \) lie on plane \( \Pi_3 \). It is given that the distance \( PR = 5 \) cm.
(c) (i) Using an appropriate compound angle identity, show that \( \sin 75^\circ = \frac{\sqrt{2} + \sqrt{6}}{4} \). (ii) Find \( QR \), giving your answer in the form \( p\left( \sqrt{q} – 1 \right) \) cm, where \( p, q \in \mathbb{Z} \).

Most-appropriate topic codes (IB Mathematics Analysis and Approaches 2021):

AHL 3.17: Vector equations of a plane — parts (a), (b)
AHL 3.16: Vector product — part (b)
AHL 3.18: Angle between two planes — part (a)
AHL 3.10: Compound angle identities — part (c)(i)
SL 3.2: Sine rule — part (c)(ii)
▶️ Answer/Explanation

(a) Angle between planes:

Normal vectors:
\( \mathbf{n}_1 = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \), \( \mathbf{n}_2 = \begin{pmatrix} 1 \\ -1 \\ -2 \end{pmatrix} \)
Dot product: \( \mathbf{n}_1 \cdot \mathbf{n}_2 = 1 \cdot 1 + 2 \cdot (-1) + 1 \cdot (-2) = 1 – 2 – 2 = -3 \)
Magnitudes: \( |\mathbf{n}_1| = \sqrt{1 + 4 + 1} = \sqrt{6} \), \( |\mathbf{n}_2| = \sqrt{1 + 1 + 4} = \sqrt{6} \)
Let \( \phi \) be the angle between normals: \( \cos \phi = \frac{-3}{\sqrt{6} \cdot \sqrt{6}} = \frac{-3}{6} = -\frac{1}{2} \)
\( \phi = 120^\circ \) (since cosine negative in obtuse range)
Angle between planes is acute: \( \theta = 180^\circ – 120^\circ = 60^\circ \).

(b) Equation of \( \Pi_3 \):

\( \Pi_3 \) is perpendicular to \( \Pi_1 \) and \( \Pi_2 \) → normal vector of \( \Pi_3 \) is parallel to \( \mathbf{n}_1 \times \mathbf{n}_2 \).
Cross product:
\( \mathbf{n}_1 \times \mathbf{n}_2 = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & 2 & 1 \\ 1 & -1 & -2 \end{vmatrix} = \mathbf{i}(2\cdot(-2) – 1\cdot(-1)) – \mathbf{j}(1\cdot(-2) – 1\cdot1) + \mathbf{k}(1\cdot(-1) – 2\cdot1) \)
\( = \mathbf{i}(-4 + 1) – \mathbf{j}(-2 – 1) + \mathbf{k}(-1 – 2) = \begin{pmatrix} -3 \\ 3 \\ -3 \end{pmatrix} \)
Simplifies to \( \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} \) as a direction (or use \( -3 \) factor).
Equation: \( x – y + z = d \) (using simplified normal \( (1, -1, 1) \))
Substitute \( R(5, -5, 5) \): \( 5 – (-5) + 5 = 15 \) → \( d = 15 \)
Thus \( \Pi_3: x – y + z = 15 \).

(c)(i) Show \( \sin 75^\circ = \frac{\sqrt{2} + \sqrt{6}}{4} \):

\( \sin 75^\circ = \sin(30^\circ + 45^\circ) \)
\( = \sin 30^\circ \cos 45^\circ + \cos 30^\circ \sin 45^\circ \)
\( = \frac{1}{2} \cdot \frac{\sqrt{2}}{2} + \frac{\sqrt{3}}{2} \cdot \frac{\sqrt{2}}{2} \)
\( = \frac{\sqrt{2}}{4} + \frac{\sqrt{6}}{4} = \frac{\sqrt{2} + \sqrt{6}}{4} \)

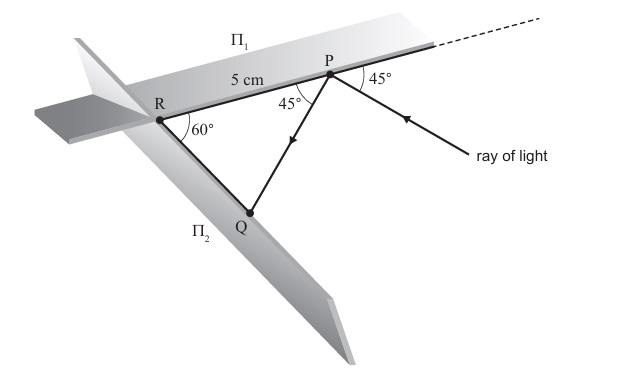
(ii) let \( x = QR \)

attempt to use the sine rule with the angles \( 75^\circ, 45^\circ \)
\(\frac{5}{\sin 75^\circ} = \frac{x}{\sin 45^\circ}\)
\(x = \frac{20}{\sqrt{2} (\sqrt{2} + \sqrt{6})} = \frac{20}{2 (1 + \sqrt{3})}\) or equivalent attempt to rationalise a denominator of the form \((\sqrt{a} + \sqrt{b})\) by multiplying numerator and denominator by \(\pm (\sqrt{a} – \sqrt{b})\) or equivalent
\(x = \frac{20 (\sqrt{2} – \sqrt{6})}{\sqrt{2} (\sqrt{2} + \sqrt{6}) (\sqrt{2} – \sqrt{6})} = \frac{20 (1 – \sqrt{3})}{2 (1 + \sqrt{3}) (1 – \sqrt{3})}\)
\(x = 5 (\sqrt{3} – 1) \, \text{cm} \quad (p = 5, \, q = 3)\)

More MAA HL Paper 1 Questions..
Scroll to Top