Question
In the diagram below, AD is perpendicular to BC.
CD = 4, BD = 2 and AD = 3. \({\rm{C}}\hat {\rm{A}}{\rm{D}} = \alpha \) and \({\rm{B}}\hat {\rm{A}}{\rm{D}} = \beta \) .
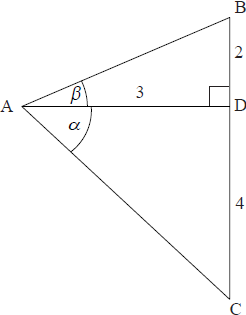
Find the exact value of \(\cos (\alpha – \beta )\) .
▶️Answer/Explanation
Markscheme
METHOD 1
\({\text{AC}} = 5\) and \(\text{AB} = \sqrt {13}\) (may be seen on diagram) (A1)
\(\cos \alpha = \frac{3}{5}\) and \(\sin \alpha = \frac{4}{5}\) (A1)
\(\cos \beta = \frac{3}{{\sqrt {13} }}\) and \(\sin \beta = \frac{2}{{\sqrt {13} }}\) (A1)
Note: If only the two cosines are correctly given award (A1)(A1)(A0).
Use of \(\cos (\alpha – \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \) (M1)
\( = \frac{3}{5} \times \frac{3}{{\sqrt {13} }} + \frac{4}{5} \times \frac{2}{{\sqrt {13} }}\) (substituting) M1
\( = \frac{{17}}{{5\sqrt {13} }}\) \(\left( { = \frac{{17\sqrt {13} }}{{65}}} \right)\) A1 N1
[6 marks]
METHOD 2
\({\text{AC}} = 5\) amd \({\text{AB}} = \sqrt {13} \) (may be seen on diagram) (A1)
Use of \(\cos (\alpha + \beta ) = \frac{{{\text{A}}{{\text{C}}^2} + {\text{A}}{{\text{B}}^2} – {\text{B}}{{\text{C}}^2}}}{{{\text{2(AC)(AB)}}}}\) (M1)
\( = \frac{{25 + 13 – 36}}{{2 \times 5 \times \sqrt {13} }}\,\,\,\,\,\left( { = \frac{1}{{5\sqrt {13} }}} \right)\) A1
Use of \(\cos (\alpha + \beta ) + \cos (\alpha – \beta ) = 2\cos \alpha \cos \beta \) (M1)
\(\cos \alpha = \frac{3}{5}\) and \(\cos \beta = \frac{3}{{\sqrt {13} }}\) (A1)
\(\cos (\alpha – \beta ) = \frac{{17}}{{5\sqrt {13} }}\,\,\,\,\,\left( { = 2 \times \frac{3}{5} \times \frac{3}{{\sqrt {13} }} – \frac{1}{{5\sqrt {13} }}} \right){\text{ }}\left( { = \frac{{17\sqrt {13} }}{{65}}} \right)\) A1 N1
[6 marks]
Question
(a) Show that \(\sin 2nx = \sin \left( {(2n + 1)x} \right)\cos x – \cos \left( {(2n + 1)x} \right)\sin x\).
(b) Hence prove, by induction, that
\[\cos x + \cos 3x + \cos 5x + \ldots + \cos \left( {(2n – 1)x} \right) = \frac{{\sin 2nx}}{{2\sin x}},\]
for all \(n \in {\mathbb{Z}^ + }{\text{, }}\sin x \ne 0\).
(c) Solve the equation \(\cos x + \cos 3x = \frac{1}{2},{\text{ }}0 < x < \pi \).
▶️Answer/Explanation
Markscheme
(a) \(\sin (2n + 1)x\cos x – \cos (2n + 1)x\sin x = \sin (2n + 1)x – x\) M1A1
\( = \sin 2nx\) AG
[2 marks]
(b) if n = 1 M1
\({\text{LHS}} = \cos x\)
\({\text{RHS}} = \frac{{\sin 2x}}{{2\sin x}} = \frac{{2\sin x\cos x}}{{2\sin x}} = \cos x\) M1
so LHS = RHS and the statement is true for n = 1 R1
assume true for n = k M1
Note: Only award M1 if the word true appears.
Do not award M1 for ‘let n = k’ only.
Subsequent marks are independent of this M1.
so \(\cos x + \cos 3x + \cos 5x + \ldots + \cos (2k – 1)x = \frac{{\sin 2kx}}{{2\sin x}}\)
if n = k + 1 then
\(\cos x + \cos 3x + \cos 5x + \ldots + \cos (2k – 1)x + \cos (2k + 1)x\) M1
\( = \frac{{\sin 2kx}}{{2\sin x}} + \cos (2k + 1)x\) A1
\( = \frac{{\sin 2kx + 2\cos (2k + 1)x\sin x}}{{2\sin x}}\) M1
\( = \frac{{\sin (2k + 1)x\cos x – \cos (2k + 1)x\sin x + 2\cos (2k + 1)x\sin x}}{{2\sin x}}\) M1
\( = \frac{{\sin (2k + 1)x\cos x + \cos (2k + 1)x\sin x}}{{2\sin x}}\) A1
\( = \frac{{\sin (2k + 2)x}}{{2\sin x}}\) M1
\( = \frac{{\sin 2(k + 1)x}}{{2\sin x}}\) A1
so if true for n = k, then also true for n = k + 1
as true for n = 1 then true for all \(n \in {\mathbb{Z}^ + }\) R1
Note: Final R1 is independent of previous work.
[12 marks]
(c) \(\frac{{\sin 4x}}{{2\sin x}} = \frac{1}{2}\) M1A1
\(\sin 4x = \sin x\)
\(4x = x \Rightarrow x = 0\) but this is impossible
\(4x = \pi – x \Rightarrow x = \frac{\pi }{5}\) A1
\(4x = 2\pi + x \Rightarrow x = \frac{{2\pi }}{3}\) A1
\(4x = 3\pi – x \Rightarrow x = \frac{{3\pi }}{5}\) A1
for not including any answers outside the domain R1
Note: Award the first M1A1 for correctly obtaining \(8{\cos ^3}x – 4\cos x – 1 = 0\) or equivalent and subsequent marks as appropriate including the answers \(\left( { – \frac{1}{2},\frac{{1 \pm \sqrt 5 }}{4}} \right)\).
[6 marks] Total [20 marks]
Question
If x satisfies the equation \(\sin \left( {x + \frac{\pi }{3}} \right) = 2\sin x\sin \left( {\frac{\pi }{3}} \right)\), show that \(11\tan x = a + b\sqrt 3 \), where a, b \( \in {\mathbb{Z}^ + }\).
▶️Answer/Explanation
Markscheme
\(\sin \left( {x + \frac{\pi }{3}} \right) = \sin x\cos \left( {\frac{\pi }{3}} \right) + \cos x\sin \left( {\frac{\pi }{3}} \right)\) (M1)
\(\sin x\cos \left( {\frac{\pi }{3}} \right) + \cos x\sin \left( {\frac{\pi }{3}} \right) = 2\sin x\sin \left( {\frac{\pi }{3}} \right)\)
\(\frac{1}{2}\sin x + \frac{{\sqrt 3 }}{2}\cos x = 2 \times \frac{{\sqrt 3 }}{2}\sin x\) A1
dividing by \(\cos x\) and rearranging M1
\(\tan x = \frac{{\sqrt 3 }}{{2\sqrt 3 – 1}}\) A1
rationalizing the denominator M1
\(11\tan x = 6 + \sqrt 3 \) A1
[6 marks]
Question
a.Show that \(\frac{{\sin 2\theta }}{{1 + \cos 2\theta }} = \tan \theta \) .[2]
b.Hence find the value of \(\cot \frac{\pi }{8}\) in the form \(a + b\sqrt 2 \) , where \(a,b \in \mathbb{Z}\). [3]
▶️Answer/Explanation
Markscheme
a.)
\(\frac{{\sin 2\theta }}{{1 + \cos 2\theta }} = \frac{{2\sin \theta \cos \theta }}{{1 + 2{{\cos }^2}\theta – 1}}\) M1
Note: Award M1 for use of double angle formulae.
\( = \frac{{2\sin \theta \cos \theta }}{{2{{\cos }^2}\theta }}\) A1
\( = \frac{{\sin \theta }}{{\cos \theta }}\)
\( = \tan \theta \) AG
[2 marks]
\(\tan \frac{\pi }{8} = \frac{{\sin \frac{\pi }{4}}}{{1 + \cos \frac{\pi }{4}}}\) (M1)
\(\cot \frac{\pi }{8} = \frac{{1 + \cos \frac{\pi }{4}}}{{\sin \frac{\pi }{4}}}\) M1
\( = \frac{{1 + \frac{{\sqrt 2 }}{2}}}{{\frac{{\sqrt 2 }}{2}}}\)
\( = 1 + \sqrt 2 \) A1
[3 marks]
Question
a.Show that \(\frac{{\sin 2\theta }}{{1 + \cos 2\theta }} = \tan \theta \) . [2]
b. Hence find the value of \(\cot \frac{\pi }{8}\) in the form \(a + b\sqrt 2 \) , where \(a,b \in \mathbb{Z}\).[3]
▶️Answer/Explanation
Markscheme
a.
\(\frac{{\sin 2\theta }}{{1 + \cos 2\theta }} = \frac{{2\sin \theta \cos \theta }}{{1 + 2{{\cos }^2}\theta – 1}}\) M1
Note: Award M1 for use of double angle formulae.
\( = \frac{{2\sin \theta \cos \theta }}{{2{{\cos }^2}\theta }}\) A1
\( = \frac{{\sin \theta }}{{\cos \theta }}\)
\( = \tan \theta \) AG
[2 marks]
\(\tan \frac{\pi }{8} = \frac{{\sin \frac{\pi }{4}}}{{1 + \cos \frac{\pi }{4}}}\) (M1)
\(\cot \frac{\pi }{8} = \frac{{1 + \cos \frac{\pi }{4}}}{{\sin \frac{\pi }{4}}}\) M1
\( = \frac{{1 + \frac{{\sqrt 2 }}{2}}}{{\frac{{\sqrt 2 }}{2}}}\)
\( = 1 + \sqrt 2 \) A1
[3 marks]
Question
Let \(f(x) = \frac{{\sin 3x}}{{\sin x}} – \frac{{\cos 3x}}{{\cos x}}\).
a. For what values of x does \(f(x)\) not exist?[2]
b. Simplify the expression \(\frac{{\sin 3x}}{{\sin x}} – \frac{{\cos 3x}}{{\cos x}}\). [5]
▶️Answer/Explanation
Markscheme
a.
\(\cos x = 0{\text{, }}\sin x = 0\) (M1)
\(x = \frac{{n\pi }}{2},n \in \mathbb{Z}\) A1
EITHER
\(\frac{{\sin 3x\cos x – \cos 3x\sin x}}{{\sin x\cos x}}\) M1 A1
\( = \frac{{\sin (3x – x)}}{{\frac{1}{2}\sin 2x}}\) A1 A1
\( = 2\) A1
OR
\(\frac{{\sin 2x\cos x + \cos 2x\sin x}}{{\sin x}} – \frac{{\cos 2x\cos x – \sin 2x\sin x}}{{\cos x}}\) M1
\( = \frac{{2\sin x{{\cos }^2}x + 2{{\cos }^2}x\sin x – \sin x}}{{\sin x}} – \frac{{2{{\cos }^3}x – \cos x – {{\sin }^2}x\cos x}}{{\cos x}}\) A1 A1
\( = 4{\cos ^2}x – 1 – 2{\cos ^2}x + 1 + 2{\sin ^2}x\) A1
\( = 2{\cos ^2}x + 2{\sin ^2}x\)
\( = 2\) A1
[5 marks]
Question
Show that \(\frac{{\cos A + \sin A}}{{\cos A – \sin A}} = \sec 2A + \tan 2A\) .
▶️Answer/Explanation
Markscheme
METHOD 1
\(\frac{{\cos A + \sin A}}{{\cos A – \sin A}} = \sec 2A + \tan 2A\)
consider right hand side
\(\sec 2A + \tan 2A = \frac{1}{{\cos 2A}} + \frac{{\sin 2A}}{{\cos 2A}}\) M1A1
\( = \frac{{{{\cos }^2}A + 2\sin A\cos A + {{\sin }^2}A}}{{{{\cos }^2}A – {{\sin }^2}A}}\) A1A1
Note: Award A1 for recognizing the need for single angles and A1 for recognizing \({\cos ^2}A + {\sin ^2}A = 1\) .
\( = \frac{{{{(\cos A + \sin A)}^2}}}{{(\cos A + \sin A)(\cos A – \sin A)}}\) M1A1
\( = \frac{{\cos A + \sin A}}{{\cos A – \sin A}}\) AG
METHOD 2
\(\frac{{\cos A + \sin A}}{{\cos A – \sin A}} = \frac{{{{(\cos A + \sin A)}^2}}}{{(\cos A + \sin A)(\cos A – \sin A)}}\) M1A1
\( = \frac{{{{\cos }^2}A + 2\sin A\cos A + {{\sin }^2}A}}{{{{\cos }^2}A – {{\sin }^2}A}}\) A1A1
Note: Award A1 for correct numerator and A1 for correct denominator.
\( = \frac{{1 + \sin 2A}}{{\cos 2A}}\) M1A1
\( = \sec 2A + \tan 2A\) AG
[6 marks]
Question
Consider the curve defined by the equation \({x^2} + \sin y – xy = 0\) .
a. Find the gradient of the tangent to the curve at the point \((\pi ,{\text{ }}\pi )\) . [6]
b. Hence, show that \(\tan \theta = \frac{1}{{1 + 2\pi }}\), where \(\theta \) is the acute angle between the tangent to the curve at \((\pi ,{\text{ }}\pi )\) and the line y = x . [3]
▶️Answer/Explanation
Markscheme
a.
attempt to differentiate implicitly M1
\(2x + \cos y\frac{{{\text{d}}y}}{{{\text{d}}x}} – y – x\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) A1A1
Note: A1 for differentiating \({x^2}\) and sin y ; A1 for differentiating xy.
substitute x and y by \(\pi \) M1
\(2\pi – \frac{{{\text{d}}y}}{{{\text{d}}x}} – \pi – \pi \frac{{{\text{d}}y}}{{{\text{d}}x}} = 0 \Rightarrow \frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{\pi }{{1 + \pi }}\) M1A1
Note: M1 for attempt to make dy/dx the subject. This could be seen earlier.
[6 marks]
\(\theta = \frac{\pi }{4} – \arctan \frac{\pi }{{1 + \pi }}\) (or seen the other way) M1
\(\tan \theta = \tan \left( {\frac{\pi }{4} – \arctan \frac{\pi }{{1 + \pi }}} \right) = \frac{{1 – \frac{\pi }{{1 + \pi }}}}{{1 + \frac{\pi }{{1 + \pi }}}}\) M1A1
\(\tan \theta = \frac{1}{{1 + 2\pi }}\) AG [3 marks]
Question
The function f is defined by \(f(x) = \frac{1}{{4{x^2} – 4x + 5}}\).
a. Express \(4{x^2} – 4x + 5\) in the form \(a{(x – h)^2} + k\) where a, h, \(k \in \mathbb{Q}\).[2]
b.The graph of \(y = {x^2}\) is transformed onto the graph of \(y = 4{x^2} – 4x + 5\). Describe a sequence of transformations that does this, making the order of transformations clear.[3]
c. Sketch the graph of \(y = f(x)\).[2]
d.Find the range of f.[2]
e. By using a suitable substitution show that \(\int {f(x){\text{d}}x = \frac{1}{4}\int {\frac{1}{{{u^2} + 1}}{\text{d}}u} } \). [3]
f. Prove that \(\int_1^{3.5} {\frac{1}{{4{x^2} – 4x + 5}}{\text{d}}x = \frac{\pi }{{16}}} \). [7]
▶️Answer/Explanation
Markscheme
a.
\(4{(x – 0.5)^2} + 4\) A1A1
Note: A1 for two correct parameters, A2 for all three correct.
[2 marks]
translation \(\left( {\begin{array}{*{20}{c}}
{0.5} \\
0
\end{array}} \right)\) (allow “0.5 to the right”) A1
stretch parallel to y-axis, scale factor 4 (allow vertical stretch or similar) A1
translation \(\left( {\begin{array}{*{20}{c}}
0 \\
4
\end{array}} \right)\) (allow “4 up”) A1
Note: All transformations must state magnitude and direction.
Note: First two transformations can be in either order.
It could be a stretch followed by a single translation of \(\left( {\begin{array}{*{20}{c}}
{0.5} \\
4
\end{array}} \right)\). If the vertical translation is before the stretch it is \(\left( {\begin{array}{*{20}{c}}
0 \\
1
\end{array}} \right)\).
[3 marks]
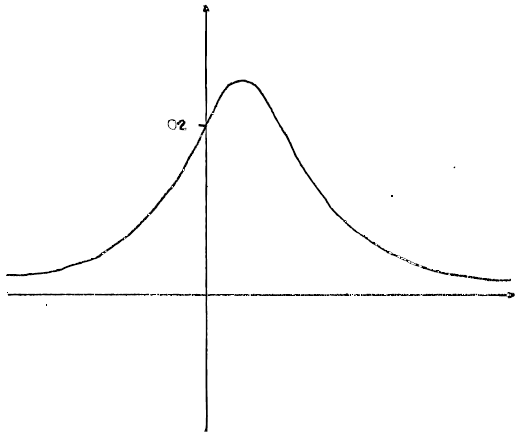
general shape (including asymptote and single maximum in first quadrant), A1
intercept \(\left( {0,\frac{1}{5}} \right)\) or maximum \(\left( {\frac{1}{2},\frac{1}{4}} \right)\) shown A1
[2 marks]
\(0 < f(x) \leqslant \frac{1}{4}\) A1A1
Note: A1 for \( \leqslant \frac{1}{4}\), A1 for \(0 < \).
[2 marks]
let \(u = x – \frac{1}{2}\) A1
\(\frac{{{\text{d}}u}}{{{\text{d}}x}} = 1\,\,\,\,\,{\text{(or d}}u = {\text{d}}x)\) A1
\(\int {\frac{1}{{4{x^2} – 4x + 5}}{\text{d}}x = \int {\frac{1}{{4{{\left( {x – \frac{1}{2}} \right)}^2} + 4}}{\text{d}}x} } \) A1
\(\int {\frac{1}{{4{u^2} + 4}}{\text{d}}u = \frac{1}{4}\int {\frac{1}{{{u^2} + 1}}{\text{d}}u} } \) AG
Note: If following through an incorrect answer to part (a), do not award final A1 mark.
[3 marks]
f. \(\int_1^{3.5} {\frac{1}{{4{x^2} – 4x + 5}}{\text{d}}x = \frac{1}{4}\int_{0.5}^3 {\frac{1}{{{u^2} + 1}}{\text{d}}u} } \) A1
Note: A1 for correct change of limits. Award also if they do not change limits but go back to x values when substituting the limit (even if there is an error in the integral).
\(\frac{1}{4}\left[ {\arctan (u)} \right]_{0.5}^3\) (M1)
\(\frac{1}{4}\left( {\arctan (3) – \arctan \left( {\frac{1}{2}} \right)} \right)\) A1
let the integral = I
\(\tan 4I = \tan \left( {\arctan (3) – \arctan \left( {\frac{1}{2}} \right)} \right)\) M1
\(\frac{{3 – 0.5}}{{1 + 3 \times 0.5}} = \frac{{2.5}}{{2.5}} = 1\) (M1)A1
\(4I = \frac{\pi }{4} \Rightarrow I = \frac{\pi }{{16}}\) A1AG
[7 marks]
Question
a. Given that \(\arctan \left( {\frac{1}{5}} \right) + \arctan \left( {\frac{1}{8}} \right) = \arctan \left( {\frac{1}{p}} \right)\), where \(p \in {\mathbb{Z}^ + }\), find p.[3]
b.Hence find the value of \(\arctan \left( {\frac{1}{2}} \right) + \arctan \left( {\frac{1}{5}} \right) + \arctan \left( {\frac{1}{8}} \right)\).[3]
▶️Answer/Explanation
Markscheme
a.)
attempt at use of \(\tan (A + B) = \frac{{\tan (A) + \tan (B)}}{{1 – \tan (A)\tan (B)}}\) M1
\(\frac{1}{p} = \frac{{\frac{1}{5} + \frac{1}{8}}}{{1 – \frac{1}{5} \times \frac{1}{8}}}{\text{ }}\left( { = \frac{1}{3}} \right)\) A1
\(p = 3\) A1
Note: the value of p needs to be stated for the final mark.
[3 marks]
\(\tan \left( {\arctan \left( {\frac{1}{2}} \right) + \arctan \left( {\frac{1}{5}} \right) + \arctan \left( {\frac{1}{8}} \right)} \right) = \frac{{\frac{1}{2} + \frac{1}{3}}}{{1 – \frac{1}{2} \times \frac{1}{3}}} = 1\) M1A1
\(\arctan \left( {\frac{1}{2}} \right) + \arctan \left( {\frac{1}{5}} \right) + \arctan \left( {\frac{1}{8}} \right) = \frac{\pi }{4}\) A1
[3 marks]
Question
a. Given that \(\arctan \left( {\frac{1}{5}} \right) + \arctan \left( {\frac{1}{8}} \right) = \arctan \left( {\frac{1}{p}} \right)\), where \(p \in {\mathbb{Z}^ + }\), find p.[3]
b. Hence find the value of \(\arctan \left( {\frac{1}{2}} \right) + \arctan \left( {\frac{1}{5}} \right) + \arctan \left( {\frac{1}{8}} \right)\). [3]
▶️Answer/Explanation
Markscheme
a.)
attempt at use of \(\tan (A + B) = \frac{{\tan (A) + \tan (B)}}{{1 – \tan (A)\tan (B)}}\) M1
\(\frac{1}{p} = \frac{{\frac{1}{5} + \frac{1}{8}}}{{1 – \frac{1}{5} \times \frac{1}{8}}}{\text{ }}\left( { = \frac{1}{3}} \right)\) A1
\(p = 3\) A1
Note: the value of p needs to be stated for the final mark. [3 marks]
\(\tan \left( {\arctan \left( {\frac{1}{2}} \right) + \arctan \left( {\frac{1}{5}} \right) + \arctan \left( {\frac{1}{8}} \right)} \right) = \frac{{\frac{1}{2} + \frac{1}{3}}}{{1 – \frac{1}{2} \times \frac{1}{3}}} = 1\) M1A1
\(\arctan \left( {\frac{1}{2}} \right) + \arctan \left( {\frac{1}{5}} \right) + \arctan \left( {\frac{1}{8}} \right) = \frac{\pi }{4}\) A1
Question
(a) Prove the trigonometric identity \(\sin (x + y)\sin (x – y) = {\sin ^2}x – {\sin ^2}y\).
(b) Given \(f(x) = \sin({x + \frac{\pi }{6}})\sin({x – \frac{\pi }{6}}),{\text{ }}x \in \left[ {0,{\text{ }}\pi } \right]\), find the range of \(f\).
(c) Given \(g(x) = \csc( {x + \frac{\pi }{6}})\csc( {x – \frac{\pi }{6}}),{\text{ }}x \in \left[ {0,{\text{ }}\pi } \right],{\text{ }}x \ne \frac{\pi }{6},{\text{ }}x \ne \frac{{5\pi }}{6}\), find the range of \(g\).
▶️Answer/Explanation
Markscheme
(a) \(\sin (x + y)\sin (x – y)\)
\( = (\sin x\cos y + \cos x\sin y)(\sin x\cos y – \cos x\sin y)\) M1A1
\( = {\sin ^2}x{\cos ^2}y + \sin x\sin y\cos x\cos y – \sin x\sin y\cos x\cos y – {\cos ^2}x{\sin ^2}y\)
\( = {\sin ^2}x{\cos ^2}y – {\cos ^2}x{\sin ^2}y\) A1
\( = {\sin ^2}x(1 – {\sin ^2}y) – {\sin ^2}y(1 – {\sin ^2}x)\) A1
\( = {\sin ^2}x – {\sin ^2}x{\sin ^2}y – {\sin ^2}y + {\sin ^2}x{\sin ^2}y\)
\( = {\sin ^2}x – {\sin ^2}y\) AG
[4 marks]
(b) \(f(x) = {\sin ^2}x – \frac{1}{4}\)
range is \(f \in \left[ { – \frac{1}{4},{\text{ }}\frac{3}{4}} \right]\) A1A1
Note: Award A1 for each end point. Condone incorrect brackets.
[2 marks]
(c) \(g(x) = \frac{1}{{{{\sin }^2}x – \frac{1}{4}}}\)
range is \(g \in \left] { – \infty ,{\text{ }} – 4} \right] \cup \left[ {\frac{4}{3},{\text{ }}\infty } \right[\) A1A1
Note: Award A1 for each part of range. Condone incorrect brackets.
[2 marks]
Total [8 marks]
Question
a.)
(i) Show that \({(1 + {\text{i}}\tan \theta )^n} + {(1 – {\text{i}}\tan \theta )^n} = \frac{{2\cos n\theta }}{{{{\cos }^n}\theta }},\;\;\;\cos \theta \ne 0\).
(ii) Hence verify that \({\text{i}}\tan \frac{{3\pi }}{8}\) is a root of the equation \({(1 + z)^4} + {(1 – z)^4} = 0,\;\;\;z \in \mathbb{C}\).
(iii) State another root of the equation \({(1 + z)^4} + {(1 – z)^4} = 0,\;\;\;z \in \mathbb{C}\). [10]
(i) Use the double angle identity \(\tan 2\theta = \frac{{2\tan \theta }}{{1 – {{\tan }^2}\theta }}\) to show that \(\tan \frac{\pi }{8} = \sqrt 2 – 1\).
(ii) Show that \(\cos 4x = 8{\cos ^4}x – 8{\cos ^2}x + 1\).
(iii) Hence find the value of \(\int_0^{\frac{\pi }{8}} {\frac{{2\cos 4x}}{{{{\cos }^2}x}}{\text{d}}x} \). [13]
▶️Answer/Explanation
Markscheme
(i) METHOD 1
\({(1 + {\text{i}}\tan \theta )^n} + {(1 – {\text{i}}\tan \theta )^n} = {\left( {1 + {\text{i}}\frac{{\sin \theta }}{{\cos \theta }}} \right)^n} + {\left( {1 – {\text{i}}\frac{{\sin \theta }}{{\cos \theta }}} \right)^n}\) M1
\( = {\left( {\frac{{\cos \theta + i\sin \theta }}{{\cos \theta }}} \right)^n} + {\left( {\frac{{\cos \theta – i\sin \theta }}{{\cos \theta }}} \right)^n}\) A1
by de Moivre’s theorem (M1)
\({\left( {\frac{{\cos \theta + i\sin \theta }}{{\cos \theta }}} \right)^n} = \frac{{\cos n\theta + i\sin n\theta }}{{{{\cos }^n}\theta }}\) A1
recognition that \(\cos \theta – i\sin \theta \) is the complex conjugate of \(\cos \theta + i\sin \theta \) (R1)
use of the fact that the operation of complex conjugation commutes with the operation of raising to an integer power:
\({\left( {\frac{{\cos \theta – i\sin \theta }}{{\cos \theta }}} \right)^n} = \frac{{\cos n\theta – i\sin n\theta }}{{{{\cos }^n}\theta }}\) A1
\({(1 + {\text{i}}\tan \theta )^n} + {(1 – {\text{i}}\tan \theta )^n} = \frac{{2\cos n\theta }}{{{{\cos }^n}\theta }}\) AG
METHOD 2
\({(1 + {\text{i}}\tan \theta )^n} + {(1 – {\text{i}}\tan \theta )^n} = {(1 + {\text{i}}\tan \theta )^n} + {\left( {1 + {\text{i}}\tan ( – \theta )} \right)^n}\) (M1)
\( = \frac{{{{(\cos \theta + i\sin \theta )}^n}}}{{{{\cos }^n}\theta }} + \frac{{{{\left( {\cos ( – \theta ) + i\sin ( – \theta )} \right)}^n}}}{{{{\cos }^n}\theta }}\) M1A1
Note: Award M1 for converting to cosine and sine terms.
use of de Moivre’s theorem (M1)
\( = \frac{1}{{{{\cos }^n}\theta }}\left( {\cos n\theta + {\text{i}}\sin n\theta + \cos ( – n\theta ) + {\text{i}}\sin ( – n\theta )} \right)\) A1
\( = \frac{{2\cos n\theta }}{{{{\cos }^2}\theta }}\;\;\;{\text{as}}\;\;\;\cos ( – n\theta ) = \cos n\theta \;\;\;{\text{and}}\;\;\;\sin ( – n\theta ) = – \sin n\theta \) R1AG
(ii) \({\left( {1 + {\text{i}}\tan \frac{{3\pi }}{8}} \right)^4} + {\left( {1 – {\text{i}}\tan \frac{{3\pi }}{8}} \right)^4} = \frac{{2\cos \left( {4 \times \frac{{3\pi }}{8}} \right)}}{{{{\cos }^4}\frac{{3\pi }}{8}}}\) (A1)
\( = \frac{{2\cos \frac{{3\pi }}{2}}}{{{{\cos }^4}\frac{{3\pi }}{8}}}\) A1
\( = 0\;\;\;{\text{as}}\;\;\;\cos \frac{{3\pi }}{2} = 0\) R1
Note: The above working could involve theta and the solution of \(\cos (4\theta ) = 0\).
so \({\text{i}}\tan \frac{{3\pi }}{8}\) is a root of the equation AG
(iii) either \( – {\text{i}}\tan \frac{{3\pi }}{8}\;\;\;{\text{or}}\;\;\; – {\text{i}}\tan \frac{\pi }{8}\;\;\;{\text{or}}\;\;\;{\text{i}}\tan \frac{\pi }{8}\) A1
Note: Accept \({\text{i}}\tan \frac{{5\pi }}{8}\;\;\;{\text{or}}\;\;\;{\text{i}}\tan \frac{{7\pi }}{8}\).
Accept \( – \left( {1 + \sqrt 2 } \right){\text{i}}\;\;\;{\text{or}}\;\;\;\left( {1 – \sqrt 2 } \right){\text{i}}\;\;\;{\text{or}}\;\;\;\left( { – 1 + \sqrt 2 } \right){\text{i}}\). [10 marks]
(i) \(\tan \frac{\pi }{4} = \frac{{2\tan \frac{\pi }{8}}}{{1 – {{\tan }^2}\frac{\pi }{8}}}\) (M1)
\({\tan ^2}\frac{\pi }{8} + 2\tan \frac{\pi }{8} – 1 = 0\) A1
let \(t = \tan \frac{\pi }{8}\)
attempting to solve \({t^2} + 2t – 1 = 0\;\;\;{\text{for}}\;\;\;t\) M1
\(t = – 1 \pm \sqrt 2 \) A1
\(\frac{\pi }{8}\) is a first quadrant angle and tan is positive in this quadrant, so
\(\tan \frac{\pi }{8} > 0\) R1
\(\tan \frac{\pi }{8} = \sqrt 2 – 1\) AG
(ii) \(\cos 4x = 2{\cos ^2}2x – 1\) A1
\( = 2{\left( {2{{\cos }^2}x – 1} \right)^2} – 1\) M1
\( = 2\left( {4{{\cos }^4}x – 4{{\cos }^2}x + 1} \right) – 1\) A1
\( = 8{\cos ^4}x – 8{\cos ^2}x + 1\) AG
Note: Accept equivalent complex number derivation.
(iii) \(\int_0^{\frac{\pi }{8}} {\frac{{2\cos 4x}}{{{{\cos }^2}x}}{\text{d}}x = 2} \int_0^{\frac{\pi }{8}} {\frac{{8{{\cos }^4}x – 8{{\cos }^2}x + 1}}{{{{\cos }^2}x}}{\text{d}}x} \)
\( = 2\int_0^{\frac{\pi }{8}} {8{{\cos }^2}x – 8 + {{\sec }^2}x{\text{d}}x} \) M1
Note: The M1 is for an integrand involving no fractions.
use of \({\cos ^2}x = \frac{1}{2}(\cos 2x + 1)\) M1
\( = 2\int_0^{\frac{\pi }{8}} {4\cos 2x – 4 + {{\sec }^2}x{\text{d}}x} \) A1
\( = [4\sin 2x – 8x + 2\tan x]_0^{\frac{\pi }{8}}\) A1
\( = 4\sqrt 2 – \pi – 2\;\;\;\)(or equivalent) A1
[13 marks] Total [23 marks]
Question
a.Show that \(\sin \left( {\theta + \frac{\pi }{2}} \right) = \cos \theta \). [1]
b.Consider \(f(x) = \sin (ax)\) where \(a\) is a constant. Prove by mathematical induction that \({f^{(n)}}(x) = {a^n}\sin \left( {ax + \frac{{n\pi }}{2}} \right)\) where \(n \in {\mathbb{Z}^ + }\) and \({f^{(n)}}(x)\) represents the \({{\text{n}}^{{\text{th}}}}\) derivative of \(f(x)\).[7]
▶️Answer/Explanation
Markscheme
a.
\(\sin \left( {\theta + \frac{\pi }{2}} \right) = \sin \theta \cos \frac{\pi }{2} + \cos \theta \sin \frac{\pi }{2}\) M1
\( = \cos \theta \) AG
Note: Accept a transformation/graphical based approach. [1 mark]
consider \(n = 1,{\text{ }}f'(x) = a\cos (ax)\) M1
since \(\sin \left( {ax + \frac{\pi }{2}} \right) = \cos ax\) then the proposition is true for \(n = 1\) R1
assume that the proposition is true for \(n = k\) so \({f^{(k)}}(x) = {a^k}\sin \left( {ax + \frac{{k\pi }}{2}} \right)\) M1
\({f^{(k + 1)}}(x) = \frac{{{\text{d}}\left( {{f^{(k)}}(x)} \right)}}{{{\text{d}}x}}\;\;\;\left( { = a\left( {{a^k}\cos \left( {ax + \frac{{k\pi }}{2}} \right)} \right)} \right)\) M1
\( = {a^{k + 1}}\sin \left( {ax + \frac{{k\pi }}{2} + \frac{\pi }{2}} \right)\) (using part (a)) A1
\( = {a^{k + 1}}\sin \left( {ax + \frac{{(k + 1)\pi }}{2}} \right)\) A1
given that the proposition is true for \(n = k\) then we have shown that the proposition is true for \(n = k + 1\). Since we have shown that the proposition is true for \(n = 1\) then the proposition is true for all \(n \in {\mathbb{Z}^ + }\) R1
Note: Award final R1 only if all prior M and R marks have been awarded.
[7 marks] Total [8 marks]
Question
The following diagram shows the triangle ABC where \({\text{AB}} = 2,{\text{ AC}} = \sqrt 2 \) and \({\rm{B\hat AC}} = 15^\circ \).
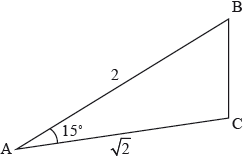
a. Expand and simplify \({\left( {1 – \sqrt 3 } \right)^2}\).[1]
b. By writing \(15^\circ \) as \(60^\circ – 45^\circ \) find the value of \(\cos (15^\circ )\).[3]
c. Find BC in the form \(a + \sqrt b \) where \(a,{\text{ }}b \in \mathbb{Z}\). [4]
▶️Answer/Explanation
Markscheme
a.)
\({\left( {1 – \sqrt 3 } \right)^2} = 4 – 2\sqrt 3 \) A1
Note: Award A0 for \(1 – 2\sqrt 3 + 3\).
[1 mark]
\(\cos (60^\circ – 45^\circ ) = \cos (60^\circ )\cos (45^\circ ) + \sin (60^\circ )\sin (45^\circ )\) M1
\( = \frac{1}{2} \times \frac{{\sqrt 2 }}{2} + \frac{{\sqrt 3 }}{2} \times \frac{{\sqrt 2 }}{2}{\text{ }}\left( {{\text{or }}\frac{1}{2} \times \frac{1}{{\sqrt 2 }} + \frac{{\sqrt 3 }}{2} \times \frac{1}{{\sqrt 2 }}} \right)\) (A1)
\( = \frac{{\sqrt 2 + \sqrt 6 }}{4}{\text{ }}\left( {{\text{or }}\frac{{1 + \sqrt 3 }}{{2\sqrt 2 }}} \right)\) A1
[3 marks]
\(B{C^2} = 2 + 4 – 2 \times \sqrt 2 \times 2\cos (15^\circ )\) M1
\( = 6 – \sqrt 2 \left( {\sqrt 2 + \sqrt 6 } \right)\)
\( = 4 – \sqrt {12} {\text{ }}\left( { = 4 – 2\sqrt 3 } \right)\) A1
\(BC = \pm \left( {1 – \sqrt 3 } \right)\) (M1)
\(BC = – 1 + \sqrt 3 \) A1
Note: Accept \(BC = \sqrt 3 – 1\).
Note: Award M1A0 for \(1 – \sqrt 3 \).
Note: Valid geometrical methods may be seen.
[4 marks]
Question
In the diagram below, AD is perpendicular to BC, CD=4, BD=2 and AD=3, CAD = α and BAD = β.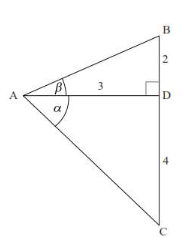
Find the exact value of cos(α-β)
▶️Answer/Explanation
Ans
AC=5 and \(AB=\sqrt{13}\) (may be seen on diagram)
\(cosα=\frac{3}{5}\) and \(sin α=\frac{4}{5}\)
\(cosβ=\frac{3}{\sqrt{13}}\)
Use of cos(α-β)=cosα cosβ+sinα sinβ
\(=\frac{3}{5}\times\frac{3}{\sqrt{13}}+\frac{4}{5}\times\frac{2}{\sqrt{13}}\) (substituting)
\(=\frac{17}{5\sqrt{13}(=\frac{1+\sqrt{13}}{65})\)
Question
Let A,B,C be the angles of a triangle. Show that tanA + tanB + tanC = tanA tanB tanC.
Hint: Difficult question indeed! Notice that A + B + c = 180o and compare tan(A + B) with tan C.
▶️Answer/Explanation
Ans
A + B + C = \(\pi\)
\(\Rightarrow A + B =\pi-C\)
\(\Rightarrow tan(A+B)=tan(\pi-C)\)
\(\Rightarrow \frac{tanA+tanB}{1-tanA tanB}=-tanC\)
\(\Rightarrow tan A+tanB=-tanC +tanA tanB tanC\)
\(\Rightarrow tanA + tan B +tanC=tanAtanBtanC\)
Question
(a) Using the formula for cos(A+B) and suitable double angle identities or any other appropriate trigonometric identity, prove the following triple angle identity
cos 3θ = 4 cos3θ – 3cosθ,
(b) Find a similar expression for sin 3θ in terms of sinθ only.
(c) Find the exact values of cosθ that satisfy the equation 3θ = 11 cos2θ.
(d) Hence or otherwise, solve the equation cos3θ = 11cos2θ, 0<x<\(\pi\).
▶️Answer/Explanation
Ans
(a) cos3θ = cos(2θ + θ) = cos 2θcosθ – sin 2θsinθ = (2cos2θ – 1)cos θ – 2sin2θcosθ
=2cos3θ – cosθ – 2(1-cos2θ)cosθ = 4cos3θ – 3cosθ
(b) Similarly \(sin3θ=3sinθ-4sin^3θ\)
(c) \(4cos^3θ-3cosθ=11cos^2θ \Leftrightarrow cosθ=0\) or cosθ=3 or cosθ=-1/4
(d) \(θ=\frac{\pi}{2}\) or \(θ=cos^{-1} (-\frac{1}{4})\)
Question
(a) Show that cos(A+B) cos(A-B)=2 cosAcosB
(b) Let \(T_n(x)\)=cos(n arccosx) where x is a real number, x∈[-1,1] and n is a positive integer.
(i) Find \(T_1(x)\).
(ii) Show that \(T_2(x)=2x^2-1\).
(c) (i) Use the result in part (a) to show that \(T_{n+1}(x)+T_{n-1}(x)=2xT_n(x)\).
(ii) Hence or otherwise, prove by induction that \(T_n(x)\) is a polynomial of degree n.
▶️Answer/Explanation
Ans
(a) cos(A+B)=cosAcosB-sinAsinB,
cos(A-B)=cosAcosB+sinAsinB
Hence cos(A+B)+cos(A-B)=2cosAcosB
(b) (i) \(T_1(x)\)=cos(arccosx)
= x
(ii) \(T2(x)\)=cos(2arccosx)
= 2 cos (arccosx) -1
= 2x2 – 1
(c) (i) \(T_{n+1}(x)+T_{n-1}(x)=cos[(n+1)arccosx]+cos[(n-1)arccosx]\)
Using part (a) with A = narccosx, B = arccosx
\(T_{n+1}(x)+T_{n-1}(x)=2cos(narccosx)cos(arccosx)\)
=2xcos(arccosx)
\(=2xT_{n}(x)\)
(ii) Let \(P_n\) be the statement: \(T_n(x)\) is a polynomial of degree, n∈\(\mathbb{Z}^+\)
\(T_1(x)=x\), a polynomial of degree one.
So \(p_2\) is true.
\(T_2(x)=2x^2-1\), is a polynomial of degree two.
So \(P_2\) is true.
Assume that \(P_k\) is true.
From part (c)(i), \(T_{k+1}(x)=2xT_k(x)-T_{k-1}(x)\)
Assume that \(p_{k-1}\) is true as well.
\(T_k(x)\) has degree k
\(\Rightarrow 2xT_k(x)\) has degree (k-1)
and as \(T_{k+1}(x)\) has degree (k-1)
\(\Rightarrow T_{k+1}(x)\) has degree (k+1)
By the principle of mathematical induction, \(p_n\) is true for all positive integers n.
