Question
The diagram below shows a curve with equation \(y = 1 + k\sin x\) , defined for \(0 \leqslant x \leqslant 3\pi \) .
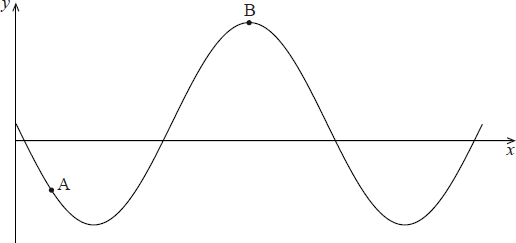
The point \({\text{A}}\left( {\frac{\pi }{6}, – 2} \right)\) lies on the curve and \({\text{B}}(a,{\text{ }}b)\) is the maximum point.
(a) Show that k = – 6 .
(b) Hence, find the values of a and b .
▶️Answer/Explanation
Markscheme
(a) \( – 2 = 1 + k\sin \left( {\frac{\pi }{6}} \right)\) M1
\( – 3 = \frac{1}{2}k\) A1
\(k = – 6\) AG N0
(b) METHOD 1
maximum \( \Rightarrow \sin x = – 1\) M1
\(a = \frac{{3\pi }}{2}\) A1
\(b = 1 – 6( – 1)\)
\( = 7\) A1 N2
METHOD 2
\(y’ = 0\) M1
\(k\cos x = 0 \Rightarrow x = \frac{\pi }{2},{\text{ }}\frac{{3\pi }}{2},{\text{ }} \ldots \)
\(a = \frac{{3\pi }}{2}\) A1
\(b = 1 – 6( – 1)\)
\( = 7\) A1 N2
Note: Award A1A1 for \(\left( {\frac{{3\pi }}{2},{\text{ }}7} \right)\) .
[5 marks]
Question
The following diagram shows the curve \(y = a\sin \left( {b(x + c)} \right) + d\), where \(a\), \(b\), \(c\) and \(d\) are all positive constants. The curve has a maximum point at \((1,{\text{ }}3.5)\) and a minimum point at \((2,{\text{ }}0.5)\).
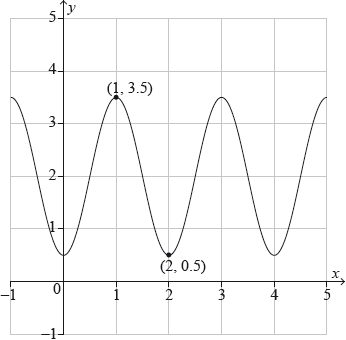
a. Write down the value of \(a\) and the value of \(d\).[2]
b.Find the value of \(b\).[2]
c.Find the smallest possible value of \(c\), given \(c > 0\). [2]
▶️Answer/Explanation
Markscheme
a. \(a = 1.5\,\,\,d = 2\) A1A1
[2 marks]
\(b = \frac{{2\pi }}{2} = \pi \) (M1)A1
[2 marks]
attempt to solve an appropriate equation or apply a horizontal translation (M1)
\(c = 1.5\) A1
Note: Do not award a follow through mark for the final A1.
Award (M1)A0 for \(c = – 0.5\).
[2 marks]
Question
Sketch the graphs of the functions
(a) f(x)=|sin 4x|, 0≤x≤\(\pi\)
(b) f(x)=|sin(\(\pi x\))|, 0≤x≤4
(c) f(x)=sin|4x|, -\(\pi\)≤x≤\(\pi\)
▶️Answer/Explanation
Ans
(a) f(x) = |sin 4x|, 0≤x≤\(\pi\)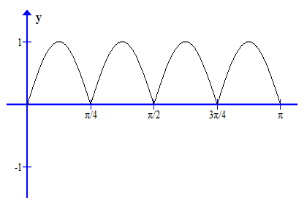
(b) f(x) =|sin(\(\pix\))|, 0≤x≤4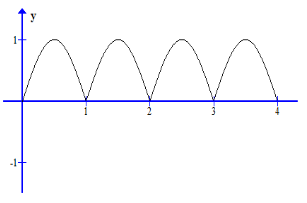
(c) f(x)=sin|4x|, -\(\pi\)≤x≤\(\pi\)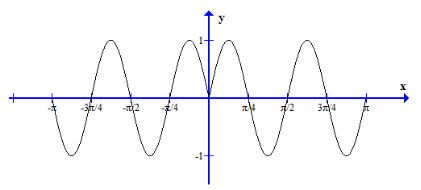
Question
Consider the function f(x) = e2x and g(x) = sin\(\frac{\pi x}{2}\).
(a) Find the period of the function fºg
(b) Find the intervals for which (fºg(x))>4
▶️Answer/Explanation
Ans
(a) fºg(x)=\(e^{2sin(\frac{\pi x}{2})}\)
Period = period of sin (\(\frac{\pi x}{2}\))
= 4 (Accept \(\frac{720o}{\pi}=229o\))
(b) 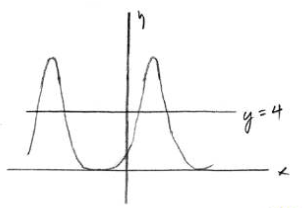
\(x\epsilon (0.488+4k,1.51+4k)(4\epsilon \mathbb{Z})(Accept x\epsilon (28.0^o+\frac{720^o}{\pi}k,86.5^o+\frac{720^o}{\pi}k))\)
