IBDP Maths SL 3.8 Solving trigonometric equations AA HL Paper 1- Exam Style Questions- New Syllabus

(a)
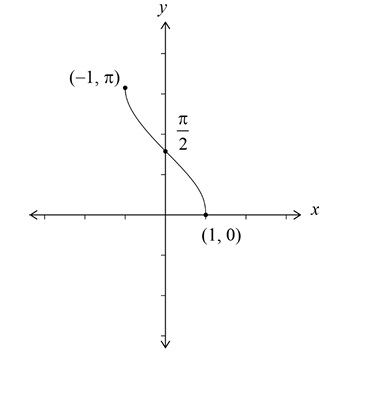
The graph of \( y = \arccos x \) is a strictly decreasing curve.
• Endpoints: \( (-1, \pi) \) and \( (1, 0) \).
• \( y \)-intercept: \( (0, \frac{\pi}{2}) \).
The curve is concave up for \( x < 0 \) and concave down for \( x > 0 \).

(b)
Let \( \alpha = \arccos x \) and \( \beta = \arccos\left( x\sqrt{3} \right) \). The given equation is \( \alpha + \beta = \frac{3\pi}{2} \).
Taking the cosine of both sides: \( \cos(\alpha + \beta) = \cos\left( \frac{3\pi}{2} \right) = 0 \).
Using the compound angle identity \( \cos(A+B) = \cos A \cos B – \sin A \sin B \):
\( \cos\alpha \cos\beta – \sin\alpha \sin\beta = 0 \).
Since \( \cos\alpha = x \) and \( \cos\beta = x\sqrt{3} \), and knowing \( \sin\theta \ge 0 \) for the range of \( \arccos \):
\( x \cdot x\sqrt{3} = \sqrt{1-x^2} \cdot \sqrt{1-3x^2} \).
Squaring both sides: \( 3x^4 = (1-x^2)(1-3x^2) \).
\( 3x^4 = 1 – 4x^2 + 3x^4 \implies 4x^2 = 1 \implies x = \pm \frac{1}{2} \).
Validation:
For \( x = \frac{1}{2} \), both \( \arccos \) values are acute, so their sum cannot be \( \frac{3\pi}{2} \).
For \( x = -\frac{1}{2} \): \( \arccos(-\frac{1}{2}) + \arccos(-\frac{\sqrt{3}}{2}) = \frac{2\pi}{3} + \frac{5\pi}{6} = \frac{9\pi}{6} = \frac{3\pi}{2} \).
\( \boxed{x = -\frac{1}{2}} \)