Question
A Ferris wheel with diameter 110 metres rotates at a constant speed. The lowest point on the wheel is 10 metres above the ground, as shown on the following diagram. P is a point on the wheel. The wheel starts moving with P at the lowest point and completes one revolution in 20 minutes.
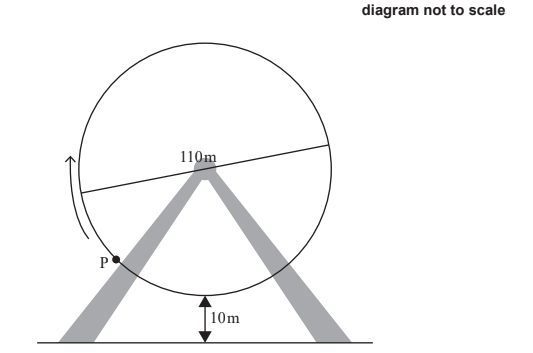
The height, h metres, of P above the ground after t minutes is given by h(t) = a cos(bt) + c, where a, b, c ∈ R.
Find the values of a , b and c .
▶️Answer/Explanation
Ans:
Amplitude is \(\frac{110}{2}\)=55
a = -55
c = 65
\(\frac{2\pi }{b}\)= 20
Or
-55cos (20b)+65=10
b= \(\frac{\pi }{10}\)(=0.314)
Question
A system of equations is given by
\[\cos x + \cos y = 1.2\]
\[\sin x + \sin y = 1.4{\text{ .}}\]
(a) For each equation express y in terms of x.
(b) Hence solve the system for \(0 < x < \pi ,{\text{ }}0 < y < \pi \) .
▶️Answer/Explanation
Markscheme
(a) \(y = \arccos (1.2 – \cos x)\) A1
\(y = \arcsin (1.4 – \sin x)\) A1
(b) The solutions are
x = 1.26, y = 0.464 A1A1
x = 0.464, y = 1.26 A1A1
[6 marks]
Examiners report
The majority of candidates obtained the first two marks. Candidates who used their GDC to solve this question did so successfully, although few candidates provided a sketch as the rubric requires. Attempts to use “solver” only gave one solution.
Some candidates did not give the solutions as coordinate pairs, but simply stated the x and y values.
Question
a.Given that \(\arctan \frac{1}{2} – \arctan \frac{1}{3} = \arctan a,{\text{ }}a \in {\mathbb{Q}^ + }\), find the value of a.[3]
b.Hence, or otherwise, solve the equation \(\arcsin x = \arctan a\).[2]
▶️Answer/Explanation
Markscheme
\(\tan \left( {\arctan \frac{1}{2} – \arctan \frac{1}{3}} \right) = \tan (\arctan a)\) (M1)
\(a = 0.14285 \ldots = \frac{1}{7}\) (A1)A1
[3 marks]
\(\arctan \left( {\frac{1}{7}} \right) = \arcsin (x) \Rightarrow x = \sin \left( {\arctan \frac{1}{7}} \right) \approx 0.141\) (M1)A1
Note: Accept exact value of \(\left( {\frac{1}{{\sqrt {50} }}} \right)\).
[2 marks]
Examiners report
Many candidates failed to give the answer for (a) in rational form. The GDC can render the answer in this form as well as the decimal approximation, but this was obviously missed by many candidates.
(b) was generally answered successfully.
Question
The function \(f(x) = 3\sin x + 4\cos x\) is defined for \(0 < x < 2\pi \) .
Write down the coordinates of the minimum point on the graph of f .[1]
a.The points \({\text{P}}(p,{\text{ }}3)\) and \({\text{Q}}(q,{\text{ }}3){\text{, }}q > p\), lie on the graph of \(y = f(x)\) .
b.Find p and q .[2]
c.Find the coordinates of the point, on \(y = f(x)\) , where the gradient of the graph is 3.[4]
d.Find the coordinates of the point of intersection of the normals to the graph at the points P and Q.[7]
▶️Answer/Explanation
Markscheme
\((3.79, – 5)\) A1
[1 mark]
\(p = 1.57{\text{ or }}\frac{\pi }{2},{\text{ }}q = 6.00\) A1A1
[2 marks]
\(f'(x) = 3\cos x – 4\sin x\) (M1)(A1)
\(3\cos x – 4\sin x = 3 \Rightarrow x = 4.43…\) (A1)
\((y = -4)\) A1
Coordinates are \((4.43, -4)\)
[4 marks]
\({m_{{\text{normal}}}} = \frac{1}{{{m_{{\text{tangent}}}}}}\) (M1)
gradient at P is \( – 4\) so gradient of normal at P is \(\frac{1}{4}\) (A1)
gradient at Q is 4 so gradient of normal at Q is \( – \frac{1}{4}\) (A1)
equation of normal at P is \(y – 3 = \frac{1}{4}(x – 1.570…){\text{ }}({\text{or }}y = 0.25x + 2.60…)\) (M1)
equation of normal at Q is \(y – 3 = \frac{1}{4}(x – 5.999…){\text{ }}({\text{or }}y = -0.25x + \underbrace {4.499…}_{})\) (M1)
Note: Award the previous two M1 even if the gradients are incorrect in \(y – b = m(x – a)\) where \((a,b)\) are coordinates of P and Q (or in \(y = mx + c\) with c determined using coordinates of P and Q.
intersect at \((3.79,{\text{ }}3.55)\) A1A1
Note: Award N2 for 3.79 without other working.
[7 marks]
Examiners report
Candidates answered parts (a) and (b) of this question well and, although many were also successful in part (c), just a few candidates gave answers to the required level of accuracy. Part d) was rather challenging for many candidates. The most common errors among the candidates who attempted this question were the confusion between tangents and normals and incorrect final answers due to premature rounding.
Candidates answered parts (a) and (b) of this question well and, although many were also successful in part (c), just a few candidates gave answers to the required level of accuracy. Part d) was rather challenging for many candidates. The most common errors among the candidates who attempted this question were the confusion between tangents and normals and incorrect final answers due to premature rounding.
Candidates answered parts (a) and (b) of this question well and, although many were also successful in part (c), just a few candidates gave answers to the required level of accuracy. Part d) was rather challenging for many candidates. The most common errors among the candidates who attempted this question were the confusion between tangents and normals and incorrect final answers due to premature rounding.
Candidates answered parts (a) and (b) of this question well and, although many were also successful in part (c), just a few candidates gave answers to the required level of accuracy. Part d) was rather challenging for many candidates. The most common errors among the candidates who attempted this question were the confusion between tangents and normals and incorrect final answers due to premature rounding.
Question
Compactness is a measure of how compact an enclosed region is.
The compactness, \(C\) , of an enclosed region can be defined by \(C = \frac{{4A}}{{\pi {d^2}}}\), where \(A\) is the area of the region and \(d\) is the maximum distance between any two points in the region.
For a circular region, \(C = 1\).
Consider a regular polygon of \(n\) sides constructed such that its vertices lie on the circumference of a circle of diameter \(x\) units.
a.If \(n > 2\) and even, show that \(C = \frac{n}{{2\pi }}\sin \frac{{2\pi }}{n}\).[3]
b.If \(n > 1\) and odd, it can be shown that \(C = \frac{{n\sin \frac{{2\pi }}{n}}}{{\pi \left( {1 + \cos \frac{\pi }{n}} \right)}}\).
Find the regular polygon with the least number of sides for which the compactness is more than \(0.99\).[4]
c.If \(n > 1\) and odd, it can be shown that \(C = \frac{{n\sin \frac{{2\pi }}{n}}}{{\pi \left( {1 + \cos \frac{\pi }{n}} \right)}}\).
Comment briefly on whether C is a good measure of compactness.[1]
▶️Answer/Explanation
Markscheme
each triangle has area \(\frac{1}{8}{x^2}\sin \frac{{2\pi }}{n}\;\;\;({\text{use of }}\frac{1}{2}ab\sin C)\) (M1)
there are \(n\) triangles so \(A = \frac{1}{8}n{x^2}\sin \frac{{2\pi }}{n}\) A1
\(C = \frac{{4\left( {\frac{1}{8}n{x^2}\sin \frac{{2\pi }}{n}} \right)}}{{\pi {n^2}}}\) A1
so \(C = \frac{n}{{2\pi }}\sin \frac{{2\pi }}{n}\) AG
[3 marks]
attempting to find the least value of \(n\) such that \(\frac{n}{{2\pi }}\sin \frac{{2\pi }}{n} > 0.99\) (M1)
\(n = 26\) A1
attempting to find the least value of \(n\) such that \(\frac{{n\sin \frac{{2\pi }}{n}}}{{\pi \left( {1 + \cos \frac{\pi }{n}} \right)}} > 0.99\) (M1)
\(n = 21\) (and so a regular polygon with 21 sides) A1
Note: Award (M0)A0(M1)A1 if \(\frac{n}{{2\pi }}\sin \frac{{2\pi }}{n} > 0.99\) is not considered and \(\frac{{n\sin \frac{{2\pi }}{n}}}{{\pi \left( {1 + \cos \frac{\pi }{n}} \right)}} > 0.99\) is correctly considered.
Award (M1)A1(M0)A0 for \(n = 26\).
[4 marks]
EITHER
for even and odd values of n, the value of C seems to increase towards the limiting value of the circle \((C = 1)\) ie as n increases, the polygonal regions get closer and closer to the enclosing circular region R1
OR
the differences between the odd and even values of n illustrate that this measure of compactness is not a good one. R1
Question
The function \(f(x) = 3\sin x + 4\cos x\) is defined for \(0 < x < 2\pi \) .
a.Write down the coordinates of the minimum point on the graph of f .[1]
b.The points \({\text{P}}(p,{\text{ }}3)\) and \({\text{Q}}(q,{\text{ }}3){\text{, }}q > p\), lie on the graph of \(y = f(x)\) .
Find p and q .[2]
c.Find the coordinates of the point, on \(y = f(x)\) , where the gradient of the graph is 3.[4]
d.Find the coordinates of the point of intersection of the normals to the graph at the points P and Q.[7]
▶️Answer/Explanation
Markscheme
\((3.79, – 5)\) A1
[1 mark]
\(p = 1.57{\text{ or }}\frac{\pi }{2},{\text{ }}q = 6.00\) A1A1
[2 marks]
\(f'(x) = 3\cos x – 4\sin x\) (M1)(A1)
\(3\cos x – 4\sin x = 3 \Rightarrow x = 4.43…\) (A1)
\((y = -4)\) A1
Coordinates are \((4.43, -4)\)
[4 marks]
\({m_{{\text{normal}}}} = \frac{1}{{{m_{{\text{tangent}}}}}}\) (M1)
gradient at P is \( – 4\) so gradient of normal at P is \(\frac{1}{4}\) (A1)
gradient at Q is 4 so gradient of normal at Q is \( – \frac{1}{4}\) (A1)
equation of normal at P is \(y – 3 = \frac{1}{4}(x – 1.570…){\text{ }}({\text{or }}y = 0.25x + 2.60…)\) (M1)
equation of normal at Q is \(y – 3 = \frac{1}{4}(x – 5.999…){\text{ }}({\text{or }}y = -0.25x + \underbrace {4.499…}_{})\) (M1)
Note: Award the previous two M1 even if the gradients are incorrect in \(y – b = m(x – a)\) where \((a,b)\) are coordinates of P and Q (or in \(y = mx + c\) with c determined using coordinates of P and Q.
intersect at \((3.79,{\text{ }}3.55)\) A1A1
Note: Award N2 for 3.79 without other working.
Question
a.Solve the equation \(3{\cos ^2}x – 8\cos x + 4 = 0\), where \(0 \leqslant x \leqslant 180^\circ \), expressing your answer(s) to the nearest degree.[3]
b.Find the exact values of \(\sec x\) satisfying the equation \(3{\sec ^4}x – 8{\sec ^2}x + 4 = 0\).[3]
▶️Answer/Explanation
Markscheme
attempting to solve for \(\cos x\) or for u where \(u = \cos x\) or for x graphically. (M1)
EITHER
\(\cos x = \frac{2}{3}{\text{ (and 2)}}\) (A1)
OR
\(x = 48.1897 \ldots ^\circ \) (A1)
THEN
\(x = 48^\circ \) A1
Note: Award (M1)(A1)A0 for \(x = 48^\circ ,{\text{ }}132^\circ \).
Note: Award (M1)(A1)A0 for 0.841 radians.
[3 marks]
attempting to solve for \(\sec x\) or for \(v\) where \(v = \sec x\). (M1)
\(\sec x = \pm \sqrt 2 {\text{ }}\left( {{\text{and }} \pm \sqrt {\frac{2}{3}} } \right)\) (A1)
\(\sec x = \pm \sqrt 2 \) A1
[3 marks]
Question
The shaded region S is enclosed between the curve \(y = x + 2\cos x\), for \(0 \leqslant x \leqslant 2\pi \), and the line \(y = x\), as shown in the diagram below.
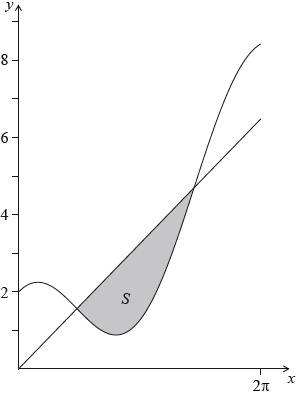
a.Find the coordinates of the points where the line meets the curve.[3]
(i) Write down an integral that represents the volume \(V\) of the solid.
(ii) Find the volume \(V\).[5]
▶️Answer/Explanation
Markscheme
(a) \(\frac{\pi }{2}(1.57),{\text{ }}\frac{{3\pi }}{2}(4.71)\) A1A1
hence the coordinates are \(\left( {\frac{\pi }{2},{\text{ }}\frac{\pi }{2}} \right),{\text{ }}\left( {\frac{{3\pi }}{2},{\text{ }}\frac{{3\pi }}{2}} \right)\) A1
[3 marks]
(i) \(\pi \int_{\frac{\pi }{2}}^{\frac{{3\pi }}{2}} {\left( {{x^2} – {{(x + 2\cos x)}^2}} \right){\text{d}}x} \) A1A1A1
Note: Award A1 for \({x^2} – {(x + 2\cos x)^2}\), A1 for correct limits and A1 for \(\pi \).
(ii) \(6{\pi ^2}{\text{ }}( = 59.2)\) A2
Notes: Do not award ft from (b)(i).
[5 marks]
Examiners report
[N/A]
[N/A]
Question
a.In triangle \(ABC\),
\(3\sin B + 4\cos C = 6\) and
\(4\sin C + 3\cos B = 1\).
Show that \(\sin (B + C) = \frac{1}{2}\).[6]
Robert conjectures that \({\rm{C\hat AB}}\) can have two possible values.
Show that Robert’s conjecture is incorrect by proving that \({\rm{C\hat AB}}\) has only one possible value.[5]
▶️Answer/Explanation
Markscheme
METHOD 1
squaring both equations M1
\(9{\sin ^2}B + 24\sin B\cos C + 16{\cos ^2}C = 36\) (A1)
\(9{\cos ^2}B + 24\cos B\sin C + 16{\sin ^2}C = 1\) (A1)
adding the equations and using \({\cos ^2}\theta + {\sin ^2}\theta = 1\) to obtain \(9 + 24\sin (B + C) + 16 = 37\) M1
\(24(\sin B\cos C + \cos B\sin C) = 12\) A1
\(24\sin (B + C) = 12\) (A1)
\(\sin (B + C) = \frac{1}{2}\) AG
METHOD 2
substituting for \(\sin B\) and \(\cos B\) to obtain
\(\sin (B + C) = \left( {\frac{{6 – 4\cos C}}{3}} \right)\cos C + \left( {\frac{{1 – 4\sin C}}{3}} \right)\sin C\) M1
\( = \frac{{6\cos C + \sin C – 4}}{3}\;\;\;\)(or equivalent) A1
substituting for \(\sin C\) and \(\cos C\) to obtain
\(\sin (B + C) = \sin B\left( {\frac{{6 – 3\sin B}}{4}} \right) + \cos B\left( {\frac{{1 – 3\cos B}}{4}} \right)\) M1
\( = \frac{{\cos B + 6\sin B – 3}}{4}\;\;\;\)(or equivalent) A1
Adding the two equations for \(\sin (B + C)\):
\(2\sin (B + C) = \frac{{(18\sin B + 24\cos C) + (4\sin C + 3\cos B) – 25}}{{12}}\) A1
\(\sin (B + C) = \frac{{36 + 1 – 25}}{{24}}\) (A1)
\(\sin (B + C) = \frac{1}{2}\) AG
METHOD 3
substituting \(\sin B\) and \(\sin C\) to obtain
\(\sin (B + C) = \left( {\frac{{6 – 4\cos C}}{3}} \right)\cos C + \cos B\left( {\frac{{1 – 3\cos B}}{4}} \right)\) M1
substituting for \(\cos B\) and \(\cos B\) to obtain
\(\sin (B + C) = \sin B\left( {\frac{{6 – 3\sin B}}{4}} \right) + \left( {\frac{{1 – 4\sin C}}{3}} \right)\sin C\) M1
Adding the two equations for \(\sin (B + C)\):
\(2\sin (B + C) = \frac{{6\cos C + \sin C – 4}}{3} + \frac{{6\sin B + \cos B – 3}}{4}\;\;\;\)(or equivalent) A1A1
\(2\sin (B + C) = \frac{{(18\sin B + 24\cos C) + (4\sin C + 3\cos B) – 25}}{{12}}\) A1
\(\sin (B + C) = \frac{{36 + 1 – 25}}{{24}}\) (A1)
\(\sin (B + C) = \frac{1}{2}\) AG
[6 marks]
\(\sin A = \sin \left( {180^\circ – (B + C)} \right)\) so \(\sin A = \sin (B + C)\) R1
\(\sin (B + C) = \frac{1}{2} \Rightarrow \sin A = \frac{1}{2}\) A1
\( \Rightarrow A = 30^\circ \) or \(A = 150^\circ \) A1
if \(A = 150^\circ \), then \(B < 30^\circ \) R1
for example, \(3\sin B + 4\cos C < \frac{3}{2} + 4 < 6\), ie a contradiction R1
only one possible value \((A = 30^\circ )\) AG
[5 marks]
Total [11 marks]
