IB Mathematics SL 3.2 Use of sine, cosine and tangent ratios AA SL Paper 1- Exam Style Questions- New Syllabus
Question
(ii) Find an expression for \( h \) in terms of \( r \) and \( \theta \).
Most-appropriate topic codes (Mathematics: analysis and approaches guide):
• SL 3.2: Use of sine, cosine and tangent ratios to find the sides and angles of right-angled triangles — Part a, c
• SL 3.6: The Pythagorean identity \( \cos^2\theta + \sin^2\theta = 1 \) — Part b
▶️ Answer/Explanation
(a)(i) Show \( R = r\cos\theta \):
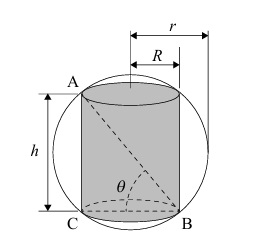
In right triangle \( ABC \) (right-angled at \( C \)):
\( AB = 2r \) (diameter of sphere)
\( BC = 2R \) (diameter of cylinder base)
From \( \triangle ABC \): \( \cos\theta = \frac{BC}{AB} = \frac{2R}{2r} = \frac{R}{r} \)
Thus, \( \boxed{R = r\cos\theta} \).
(a)(ii) Expression for \( h \):
Height \( h = AC \).
Using sine in \( \triangle ABC \): \( \sin\theta = \frac{AC}{AB} = \frac{h}{2r} \)
Thus, \( \boxed{h = 2r\sin\theta} \).
(b) Surface area \( S \) of cylinder:
Total surface area = \( 2 \times \text{base area} + \text{curved surface area} \)
\( S = 2\pi R^2 + 2\pi R h \)
Substitute \( R = r\cos\theta \) and \( h = 2r\sin\theta \):
\( S = 2\pi (r\cos\theta)^2 + 2\pi (r\cos\theta)(2r\sin\theta) \)
\( S = 2\pi r^2\cos^2\theta + 4\pi r^2\sin\theta\cos\theta \)
\( S = 2\pi r^2(\cos^2\theta + 2\sin\theta\cos\theta) \)
Using the identity \( \cos^2\theta = 1 – \sin^2\theta \):
\( S = 2\pi r^2(1 – \sin^2\theta + 2\sin\theta\cos\theta) \)
\( \boxed{S = 2\pi r^2(1 + 2\sin\theta\cos\theta – \sin^2\theta)} \).
(c) Show \( \tan\theta = 2 \):
Surface area of sphere = \( 4\pi r^2 \).
Given: \( 4\pi r^2 = 2S \)
\( 4\pi r^2 = 2[2\pi r^2(1 + 2\sin\theta\cos\theta – \sin^2\theta)] \)
\( 4\pi r^2 = 4\pi r^2(1 + 2\sin\theta\cos\theta – \sin^2\theta) \)
Divide by \( 4\pi r^2 \):
\( 1 = 1 + 2\sin\theta\cos\theta – \sin^2\theta \)
\( \sin^2\theta – 2\sin\theta\cos\theta = 0 \)
\( \sin\theta(\sin\theta – 2\cos\theta) = 0 \)
Since \( \sin\theta \neq 0 \):
\( \sin\theta = 2\cos\theta \)
\( \boxed{\tan\theta = 2} \).
(d) Volume \( V \) in form \( p\pi r^3\sqrt{5} \):
\( V = \pi R^2 h = \pi (r\cos\theta)^2 (2r\sin\theta) = 2\pi r^3\cos^2\theta\sin\theta \).
If \( \tan\theta = 2 \), then by Pythagoras:
Opposite = 2, Adjacent = 1, Hypotenuse = \( \sqrt{1^2 + 2^2} = \sqrt{5} \).
So \( \sin\theta = \frac{2}{\sqrt{5}} \) and \( \cos\theta = \frac{1}{\sqrt{5}} \).
Substitute into \( V \):
\( V = 2\pi r^3 \left(\frac{1}{\sqrt{5}}\right)^2 \left(\frac{2}{\sqrt{5}}\right) = \frac{4\pi r^3}{5\sqrt{5}} \)
Rationalizing: \( \frac{4\pi r^3}{5\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{4\pi r^3\sqrt{5}}{25} \).
\( \boxed{V = \frac{4}{25}\pi r^3\sqrt{5}} \) where \( p = \frac{4}{25} \).