Question: [Maximum mark: 20]
Two airplanes, A and B, have position vectors with respect to an origin O given respectively by
\(r_{A} = \begin{pmatrix}19\\ -1\\ 1\end{pmatrix} +t\begin{pmatrix}-6\\ 2\\ 4\end{pmatrix}\)
\(r_{B} = \begin{pmatrix}1\\ 0\\ 12\end{pmatrix} +t\begin{pmatrix}4\\ 2\\ -2\end{pmatrix}\)
where t represents the time in minutes and 0 ≤ t ≤ 2.5.
Entries in each column vector give the displacement east of O, the displacement north of O and the distance above sea level, all measured in kilometres.
(a) Find the three-figure bearing on which airplane B is travelling.
(b) Show that airplane A travels at a greater speed than airplane B.
(c) Find the acute angle between the two airplanes’ lines of flight. Give your answer in degrees.
The two airplanes’ lines of flight cross at point P.
(d) (i) Find the coordinates of P.
(ii) Determine the length of time between the first airplane arriving at P and the second airplane arriving at P.
Let D(t) represent the distance between airplane A and airplane B for 0 ≤ t ≤ 2.5.
(e) Find the minimum value of D(t).
▶️Answer/Explanation
Ans:
(a) let \(\phi \)be the required angle (bearing)
EITHER
\(\phi = 90^{0}-arctan \frac{1}{2}\left ( =arctan2 \right )\)
Note: Award M1 for a labelled sketch.

Note: Do not accept 063.40 or 63.40 or 1.10c.





(ii) attempts to find the value of t1 – t2
t1 – t2 = \(2-\frac{3}{2}\)
0.5 minutes (30 seconds)

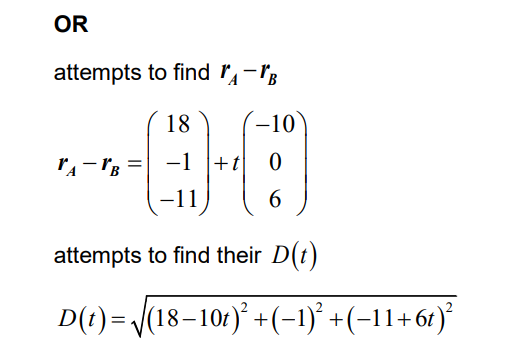
Note: Award M0M0A0 for expressions using two different time parameters.
THEN
either attempts to find the local minimum point of D (t) or attempts to find the value of t such that D’ (t) = 0 (or equivalent)
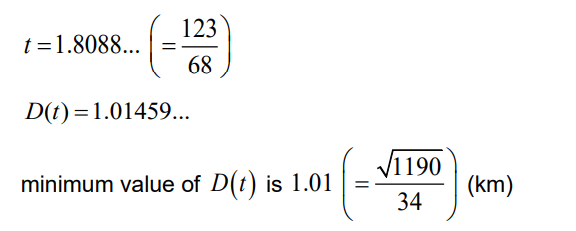
Note: Award M0 for attempts at the shortest distance between two lines.
Question
The vector equation of line \(l\) is given as \(\left( {\begin{array}{*{20}{c}}
x \\
y \\
z
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1 \\
3 \\
6
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}}
{ – 1} \\
2 \\
{ – 1}
\end{array}} \right)\) .
Find the Cartesian equation of the plane containing the line \(l\) and the point A(4, − 2, 5) .
▶️Answer/Explanation
Markscheme
EITHER
\(l\) goes through the point (1, 3, 6) , and the plane contains A(4, –2, 5)
the vector containing these two points is on the plane, i.e.
\(\left( {\begin{array}{*{20}{c}}
1 \\
3 \\
6
\end{array}} \right) – \left( {\begin{array}{*{20}{c}}
4 \\
{ – 2} \\
5
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{ – 3} \\
5 \\
1
\end{array}} \right)\) (M1)A1
\(\left( {\begin{array}{*{20}{c}}
{ – 1} \\
2 \\
{ – 1}
\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}
{ – 3} \\
5 \\
1
\end{array}} \right) = \left| {\begin{array}{*{20}{c}}
{\boldsymbol{i}}&{\boldsymbol{j}}&{\boldsymbol{k}} \\
{ – 1}&2&{ – 1} \\
{ – 3}&5&1
\end{array}} \right| = 7{\boldsymbol{i}} + 4{\boldsymbol{j}} + {\boldsymbol{k}}\) M1A1
\(\left( {\begin{array}{*{20}{c}}
4 \\
{ – 2} \\
5
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
7 \\
4 \\
1
\end{array}} \right) = 25\) (M1)
hence, Cartesian equation of the plane is \(7x + 4y + z = 25\) A1
OR
finding a third point M1
e.g. (0, 5, 5) A1
three points are (1, 3, 6), (4, –2, 5), (0, 5, 5)
equation is \(ax + by + cz = 1\)
system of equations M1
\(a + 3b + 6c = 1\)
\(4a – 2b + 5c = 1\)
\(5b + 5c = 1\)
\(a = \frac{7}{{25}}\) , \(b = \frac{4}{{25}}\) , \(c = \frac{1}{{25}}\) , from GDC M1A1
so \(\frac{7}{{25}}x + \frac{4}{{25}}y + \frac{1}{{25}}z = 1\) A1
or \(7x + 4y + z = 25\)
[6 marks]
Examiners report
There were many successful answers to this question, as would be expected. There seemed to be some students, however, that had not been taught the vector geometry section
Question
(a) Find the coordinates of the point \(A\) on \({l_1}\) and the point \(B\) on \({l_2}\) such that \(\overrightarrow {{\text{AB}}} \) is perpendicular to both \({l_1}\) and \({l_2}\) .
(b) Find \(\left| {{\text{AB}}} \right|\) .
(c) Find the Cartesian equation of the plane \(\prod \) which contains \({l_1}\) and does not intersect \({l_2}\) .
▶️Answer/Explanation
Markscheme
(a) on \({l_1}\) A(\( – 3 + 3\lambda \), \( – 4 + 2\lambda \), \(6 – 2\lambda \)) A1
on \({l_2}\) \({l_2}:r = \left( {\begin{array}{*{20}{c}}
4 \\
{ – 7} \\
3
\end{array}} \right) + \mu \left( {\begin{array}{*{20}{c}}
{ – 3} \\
4 \\
{ – 1}
\end{array}} \right)\) (M1)
\( \Rightarrow \) B(\(4 – 3\mu \), \( – 7 + 4\mu \), \( – 3 – \mu \)) A1
\(\overrightarrow {{\text{BA}}} = {\boldsymbol{a}} – {\boldsymbol{b}} = \left( {\begin{array}{*{20}{c}}
{3\lambda + 3\mu – 7} \\
{2\lambda – 4\mu + 3} \\
{ – 2\lambda + \mu + 9}
\end{array}} \right)\) (M1)A1
EITHER
\({\text{BA}} \bot {l_1} \Rightarrow {\text{BA}} \cdot \left( {\begin{array}{*{20}{c}}
3 \\
2 \\
{ – 2}
\end{array}} \right) = 0 \Rightarrow 3\left( {3\lambda + 3\mu – 7} \right) + 2\left( {2\lambda – 4\mu + 3} \right) – 2\left( { – 2\lambda + \mu + 9} \right) = 0\) M1
\( \Rightarrow 17\lambda – \mu = 33\) A1
\({\text{BA}} \bot {l_2} \Rightarrow {\text{BA}} \cdot \left( {\begin{array}{*{20}{c}}
{ – 3} \\
4 \\
{ – 1}
\end{array}} \right) = 0 \Rightarrow – 3\left( {3\lambda + 3\mu – 7} \right) + 4\left( {2\lambda – 4\mu + 3} \right) – \left( { – 2\lambda + \mu + 9} \right) = 0\) M1
\( \Rightarrow \lambda – 26\mu = – 24\) A1
solving both equations above simultaneously gives
\(\lambda = 2\); \(\mu = 1 \Rightarrow \) A(3, 0, 2), B(1, –3, –4) A1A1A1A1
OR
\(\left| {\begin{array}{*{20}{c}}
{\boldsymbol{i}}&{\boldsymbol{j}}&{\boldsymbol{k}} \\
3&2&{ – 2} \\
{ – 3}&4&{ – 1}
\end{array}} \right| = 6{\boldsymbol{i}} + 9{\boldsymbol{j}} + 18{\boldsymbol{k}}\) M1A1
so \(\overrightarrow {{\text{AB}}} = p\left( {\begin{array}{*{20}{c}}
2 \\
3 \\
6
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{3\lambda + 3\mu – 7} \\
{2\lambda – 4\mu + 3} \\
{ – 2\lambda + \mu + 9}
\end{array}} \right)\) M1A1
\({3\lambda + 3\mu – 2p = 7}\)
\({2\lambda – 4\mu – 3p = – 3}\)
\({ – 2\lambda + \mu – 6p = – 9}\)
\(\lambda = 2\), \(\mu = 1\), \(p = 1\) A1A1
A(\( – 3 + 6\), \( – 4 + 4\), \(6 – 4\)) \(=\) (\(3\), \(0\), \(2\)) A1
B(\(4 – 3\), \( – 7 + 4\), \( – 3 – 1\)) \(=\) (\(1\), \( – 3\), \( – 4\)) A1
[13 marks]
(b) \({\text{AB}} = \left( {\begin{array}{*{20}{c}}
1 \\
{ – 3} \\
{ – 4}
\end{array}} \right) – \left( {\begin{array}{*{20}{c}}
3 \\
0 \\
2
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{ – 2} \\
{ – 3} \\
{ – 6}
\end{array}} \right)\) (A1)
\(\left| {{\text{AB}}} \right| = \sqrt {{{\left( { – 2} \right)}^2} + {{\left( { – 3} \right)}^2} + {{\left( { – 6} \right)}^2}} = \sqrt {49} = 7\) M1A1
[3 marks]
(c) from (b) \(2{\boldsymbol{i}} + 3{\boldsymbol{j}} + 6{\boldsymbol{k}}\) is normal to both lines
\({l_1}\) goes through (–3, –4, 6) \( \Rightarrow \left( {\begin{array}{*{20}{c}}
{ – 3} \\
{ – 4} \\
6
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
2 \\
3 \\
6
\end{array}} \right) = 18\) M1A1
hence, the Cartesian equation of the plane through \({l_1}\) , but not \({l_2}\) , is \(2x + 3y + 6z = 18\) A1
[3 marks]
Total [19 marks]
Examiners report
There were a lot of arithmetic errors in the treatment of this question, even though it was apparent that many students did understand the methods involved. In (a) many students failed to realise that \(\overrightarrow {{\text{AB}}} \) should be a multiple of the cross product of the two direction vectors, rather than the cross product itself, and many students failed to give the final answer as coordinates.
Question
The planes \(2x + 3y – z = 5\) and \(x – y + 2z = k\) intersect in the line \(5x + 1 = 9 – 5y = – 5z\) .
Find the value of k .
▶️Answer/Explanation
Markscheme
point on line is \(x = \frac{{ – 1 – 5\lambda }}{5}{\text{, }}y = \frac{{9 + 5\lambda }}{5}{\text{, }}z = \lambda \) or similar M1A1
Note: Accept use of point on the line or elimination of one of the variables using the equations of the planes
\(\frac{{ – 1 – 5\lambda }}{5} – \frac{{9 + 5\lambda }}{5} + 2\lambda = k\) M1A1
Note: Award M1A1 if coordinates of point and equation of a plane is used to obtain linear equation in k or equations of the line are used in combination with equation obtained by elimination to get linear equation in k.
\(k = – 2\) A1
[5 marks]
Examiners report
Many different attempts were seen, sometimes with success. Unfortunately many candidates wasted time with aimless substitutions showing little understanding of the problem.
Question
A line \({L_1}\) has equation r = \(\left( \begin{array}{c} – 5\\ – 3\\2\end{array} \right) + \lambda \left( \begin{array}{c} – 1\\2\\2\end{array} \right)\).
A line \({L_2}\) passing through the origin intersects \({L_1}\) and is perpendicular to \({L_1}\).
(a) Find a vector equation of \({L_2}\).
(b) Determine the shortest distance from the origin to \({L_1}\).
▶️Answer/Explanation
Markscheme
(a) METHOD 1
for P on \({L_1},{\text{ }}\overrightarrow {{\text{OP}}} = \) \(\left( \begin{array}{c} – 5 – \lambda \\ – 3 + 2\lambda \\2 + 2\lambda \end{array} \right)\)
require \(\left( \begin{array}{c} – 5 – \lambda \\ – 3 + 2\lambda \\2 + 2\lambda \end{array} \right) \bullet \left( \begin{array}{c} – 1\\2\\2\end{array} \right) = 0\) M1
\(5 + \lambda – 6 + 4\lambda + 4 + 4\lambda = 0\) (or equivalent) A1
\(\lambda = – \frac{1}{3}\) A1
\(\therefore \overrightarrow {{\rm{OP}}} = \left( \begin{array}{c} – \frac{{14}}{3}\\ – \frac{{11}}{3}\\\frac{4}{3}\end{array} \right)\) A1
\({L_2}:\boldsymbol{r} = \mu \left( \begin{array}{c} – 14\\ – 11\\4\end{array} \right)\) A1
Note: Do not award the final A1 if \(\boldsymbol{r} =\) is not seen.
[5 marks]
METHOD 2
Calculating either \(\left| {\overrightarrow {{\text{OP}}} } \right|\) or \({\left| {\overrightarrow {{\text{OP}}} } \right|^2}\) eg
\(\left| {\overrightarrow {{\text{OP}}} } \right| = \sqrt {{{( – 5 – \lambda )}^2} + {{( – 3 + 2\lambda )}^2} + {{(2 + 2\lambda )}^2}} \) A1
\( = \sqrt {9{\lambda ^2} + 6\lambda + 38} \)
Solving either \(\frac{{\text{d}}}{{{\text{d}}\lambda }}\left( {\left| {\overrightarrow {{\text{OP}}} } \right|} \right) = 0\) or \(\frac{{\text{d}}}{{{\text{d}}\lambda }}\left( {{{\left| {\overrightarrow {{\text{OP}}} } \right|}^2}} \right) = 0\) for \(\lambda \). M1
\(\lambda = – \frac{1}{3}\) A1
\(\overrightarrow {{\rm{OP}}} = \left( \begin{array}{c} – \frac{{14}}{3}\\ – \frac{{11}}{3}\\\frac{4}{3}\end{array} \right)\) A1
\({L_2}:\boldsymbol{r} = \mu \left( \begin{array}{c} – 14\\ – 11\\4\end{array} \right)\) A1
Note: Do not award the final A1 if \(\boldsymbol{r} =\) is not seen.
[5 marks]
(b) METHOD 1
\(\left| {\overrightarrow {{\text{OP}}} } \right| = \sqrt {{{\left( { – \frac{{14}}{3}} \right)}^2} + {{\left( { – \frac{{11}}{3}} \right)}^2} + {{\left( {\frac{4}{3}} \right)}^2}} \) (M1)
\( = 6.08{\text{ }}\left( { = \sqrt {37} } \right)\) A1
METHOD 2
shortest distance = \(\frac{{\left| {\left( \begin{array}{c} – 1\\2\\2\end{array} \right) \times \left( \begin{array}{c} – 5\\ – 3\\2\end{array} \right)} \right|}}{{\left| {\left( \begin{array}{c} – 1\\2\\2\end{array} \right)} \right|}}\) (M1)
\( = \frac{{\left| {10i + 8j + 13k} \right|}}{{\sqrt {1 + 4 + 4} }}\)
\( = 6.08{\text{ }}\left( { = \sqrt {37} } \right)\) A1
[2 marks]
Total [7 marks]
Examiners report
Part (a) was not well done. Most candidates recognised the need to calculate a scalar product. Some candidates made careless sign or arithmetic errors when solving for \(\lambda \). A few candidates neglected to express their final answer in the form ‘r =’.
Candidates who were successful in answering part (a) generally answered part (b) correctly. The large majority of successful candidates calculated \(\left| {\overrightarrow {{\text{OP}}} } \right|\).
Question
Find the angle between the lines \(\frac{{x – 1}}{2} = 1 – y = 2z\) and \(x = y = 3z\) .
▶️Answer/Explanation
Markscheme
consider a vector parallel to each line,
e.g. \({\boldsymbol{u}} = \left( {\begin{array}{*{20}{c}}
4 \\
{ – 2} \\
1
\end{array}} \right)\) and \({\boldsymbol{v}} = \left( {\begin{array}{*{20}{c}}
3 \\
3 \\
1
\end{array}} \right)\) A1A1
let \(\theta \) be the angle between the lines
\(\cos \theta = \frac{{\left| {{\boldsymbol{u \times v}}} \right|}}{{\left| {\boldsymbol{u}} \right|\left| {\boldsymbol{v}} \right|}} = \frac{{\left| {12 – 6 + 1} \right|}}{{\sqrt {21} \sqrt {19} }}\) M1A1
\( = \frac{7}{{\sqrt {21} \sqrt {19} }} = 0.350…\) (A1)
so \(\theta = 69.5\) \(\left( {{\text{or }}1.21{\text{ rad or }}\arccos \left( {\frac{7}{{\sqrt {21} \sqrt {19} }}} \right)} \right)\) A1 N4
Note: Allow FT from incorrect reasonable vectors.
[6 marks]
Examiners report
Most students knew how to find the angle between two vectors, although many could not find the correct two direction vectors.
Question
Port A is defined to be the origin of a set of coordinate axes and port B is located at the point (70, 30), where distances are measured in kilometres. A ship S1 sails from port A at 10:00 in a straight line such that its position \(t\) hours after 10:00 is given by \(r = t\left( {\begin{array}{*{20}{c}}
{10} \\
{20}
\end{array}} \right)\).
A speedboat S2 is capable of three times the speed of S1 and is to meet S1 by travelling the shortest possible distance. What is the latest time that S2 can leave port B?
▶️Answer/Explanation
Markscheme
METHOD 1
equation of journey of ship S1
\({r_1} = t\left( {\begin{array}{*{20}{c}}
{10} \\
{20}
\end{array}} \right)\)
equation of journey of speedboat S2 ,setting off \(k\) minutes later
\({r_2} = \left( {\begin{array}{*{20}{c}}
{70} \\
{30}
\end{array}} \right) + \left( {t – k} \right)\left( {\begin{array}{*{20}{c}}
{ – 60} \\
{30}
\end{array}} \right)\) M1A1A1
Note: Award M1 for perpendicular direction, A1 for speed, A1 for change in parameter (e.g. by using \(t – k\) or \(T\), \(k\) being the time difference between the departure of the ships).
solve \(t\left( {\begin{array}{*{20}{c}}
{10} \\
{20}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{70} \\
{30}
\end{array}} \right) + \left( {t – k} \right)\left( {\begin{array}{*{20}{c}}
{ – 60} \\
{30}
\end{array}} \right)\) (M1)
Note: M mark is for equating their two expressions.
\(10t = 70 – 60t + 60k\)
\(20t = 30 + 30t – 30k\) M1
Note: M mark is for obtaining two equations involving two different parameters.
\(7t – 6k = 7\)
\( – t + 3k = 3\)
\(k = \frac{{28}}{{15}}\) A1
latest time is 11:52 A1
[7 marks]
METHOD 2
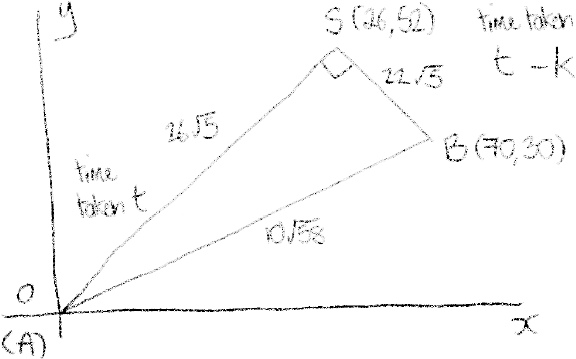
\({\text{SB}} = 22\sqrt 5 \) M1A1
(by perpendicular distance)
\({\text{SA}} = 26\sqrt 5 \) M1A1
(by Pythagoras or coordinates)
\(t = \frac{{26\sqrt 5 }}{{10\sqrt 5 }}\) A1
\(t – k = \frac{{22\sqrt 5 }}{{30\sqrt 5 }}\) A1
\(k = \frac{{28}}{{15}}\) leading to latest time 11:52 A1
[7 marks]
Examiners report
Few candidates managed to make progress on this question. Many candidates did not attempt the problem and many that did make an attempt failed to draw a diagram that would have allowed them to make further progress. There were a variety of possible solution techniques but candidates seemed unable to interpret the equation of a straight line written in vector form or find a perpendicular direction. This meant that it was very difficult for meaningful progress to be made towards a solution.
