Question
The lines l1 and l2 have the following vector equations where λ , μ ∈ \(\mathbb{R}\)
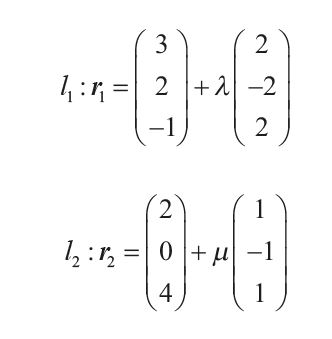
(a) Show that l1 and l2 do not intersect. [3]
(b) Find the minimum distance between l1 and l2 . [5]
▶️Answer/Explanation
Ans:
(a) We first observe that $l_1$ and $l_2$ are parallel since $\textbf{d}_1=\left(\begin{matrix}2 \\ -2 \\ 2\end{matrix}\right)=2\left(\begin{matrix}1 \\ -1 \\ 1\end{matrix}\right)=\textbf{d}_2$.
Also, since there is no value of $\lambda$ that satisfies $\left(\begin{matrix}2 \\ 0 \\ 4\end{matrix}\right)=\left(\begin{matrix}3 \\ 2 \\ -12\end{matrix}\right)+\lambda \left(\begin{matrix}2 \\ -2 \\ 2\end{matrix}\right)$, the two lines are distinct and parallel.
(b)
$$\begin{eqnarray}
\text{dist. between }l_1\text{ and }l_2 &=& \frac{\left|\left[\left(\begin{matrix}3 \\ 2 \\ -1\end{matrix}\right)-\left(\begin{matrix}2 \\ 0 \\ 4\end{matrix}\right)\right]\times\left(\begin{matrix}1 \\ -1 \\ 1\end{matrix}\right)\right|}{\left|\left(\begin{matrix}1 \\ -1 \\ 1\end{matrix}\right)\right|} \nonumber \\
= \frac{\left|\left(\begin{matrix}1 \\ 2 \\ -5\end{matrix}\right)\times\left(\begin{matrix}1 \\ -1 \\ 1\end{matrix}\right)\right|}{\sqrt{3}} \nonumber \\
= \frac{1}{\sqrt{3}}\left|\left(\begin{matrix}-3 \\ -6 \\ -3\end{matrix}\right)\right| \nonumber \\
= \frac{3}{\sqrt{3}} \left|\left(\begin{matrix}1 \\ 2 \\ 1\end{matrix}\right)\right| \nonumber \\
= 3\sqrt{2}.
\end{eqnarray}$$
Question
Two boats, A and B , move so that at time t hours, their position vectors, in kilometres, are r\(_A\) = (9t)i + (3 – 6t)j and r\(_B\) = (7 – 4t)i + (7t – 6)j .
a.Find the coordinates of the common point of the paths of the two boats.[4]
b.Show that the boats do not collide.[2]
▶️Answer/Explanation
Markscheme
METHOD 1
\(9{t_A} = 7 – 4{t_B}\) and
\(3 – 6{t_A} = – 6 + 7{t_B}\) M1A1
solve simultaneously
\({t_A} = \frac{1}{3},{\text{ }}{t_B} = 1\) A1
Note: Only need to see one time for the A1.
therefore meet at (3, 1) A1
[4 marks]
METHOD 2
path of A is a straight line: \(y = – \frac{2}{3}x + 3\) M1A1
Note: Award M1 for an attempt at simultaneous equations.
path of B is a straight line: \(y = – \frac{7}{4}x + \frac{{25}}{4}\) A1
\( – \frac{2}{3}x + 3 = – \frac{7}{4}x + \frac{{25}}{4}{\text{ }}( \Rightarrow x = 3)\)
so the common point is (3, 1) A1
[4 marks]
METHOD 1
boats do not collide because the two times \(\left( {{t_A} = \frac{1}{3},{\text{ }}{t_B} = 1} \right)\) (A1)
are different R1
[2 marks]
METHOD 2
for boat A, \(9t = 3 \Rightarrow t = \frac{1}{3}\) and for boat B, \(7 – 4t = 3 \Rightarrow t = 1\)
times are different so boats do not collide R1AG
[2 marks]
Question
Consider the plane \({\mathit{\Pi} _1}\), parallel to both lines \({L_1}\) and \({L_2}\). Point C lies in the plane \({\mathit{\Pi} _1}\).
The line \({L_3}\) has vector equation \(\boldsymbol{r} = \left( \begin{array}{l}3\\0\\1\end{array} \right) + \lambda \left( \begin{array}{c}k\\1\\ – 1\end{array} \right)\).
The plane \({\mathit{\Pi} _2}\) has Cartesian equation \(x + y = 12\).
The angle between the line \({L_3}\) and the plane \({\mathit{\Pi} _2}\) is 60°.
Given the points A(1, 0, 4), B(2, 3, −1) and C(0, 1, − 2) , find the vector equation of the line \({L_1}\) passing through the points A and B.[2]
The line \({L_2}\) has Cartesian equation \(\frac{{x – 1}}{3} = \frac{{y + 2}}{1} = \frac{{z – 1}}{{ – 2}}\).
Show that \({L_1}\) and \({L_2}\) are skew lines.[5]
Find the Cartesian equation of the plane \({\Pi _1}\).[4]
(i) Find the value of \(k\).
(ii) Find the point of intersection P of the line \({L_3}\) and the plane \({\mathit{\Pi} _2}\).[7]
▶️Answer/Explanation
Markscheme
direction vector \(\overrightarrow {{\rm{AB}}} = \left( \begin{array}{c}1\\3\\ – 5\end{array} \right)\) or \(\overrightarrow {{\rm{BA}}} = \left( \begin{array}{c} – 1\\ – 3\\5\end{array} \right)\) A1
\(\boldsymbol{r} = \left( \begin{array}{l}1\\0\\4\end{array} \right) + t\left( \begin{array}{c}1\\3\\ – 5\end{array} \right)\) or \(\boldsymbol{r} = \left( \begin{array}{c}2\\3\\ – 1\end{array} \right) + t\left( \begin{array}{c}1\\3\\ – 5\end{array} \right)\) or equivalent A1
Note: Do not award final A1 unless ‘\(\boldsymbol{r} = {\text{K}}\)’ (or equivalent) seen.
Allow FT on direction vector for final A1.
[2 marks]
both lines expressed in parametric form:
\({L_1}\):
\(x = 1 + t\)
\(y = 3t\)
\(z = 4 – 5t\)
\({L_2}\):
\(x = 1 + 3s\)
\(y = – 2 + s\) M1A1
\(z = – 2s + 1\)
Notes: Award M1 for an attempt to convert \({L_2}\) from Cartesian to parametric form.
Award A1 for correct parametric equations for \({L_1}\) and \({L_2}\).
Allow M1A1 at this stage if same parameter is used in both lines.
attempt to solve simultaneously for x and y: M1
\(1 + t = 1 + 3s\)
\(3t = – 2 + s\)
\(t = – \frac{3}{4},{\text{ }}s = – \frac{1}{4}\) A1
substituting both values back into z values respectively gives \(z = \frac{{31}}{4}\)
and \(z = \frac{3}{2}\) so a contradiction R1
therefore \({L_1}\) and \({L_1}\) are skew lines AG
[5 marks]
finding the cross product:
\(\left( \begin{array}{c}1\\3\\ – 5\end{array} \right) \times \left( \begin{array}{c}3\\1\\ – 2\end{array} \right)\) (M1)
= – i – 13j – 8k A1
Note: Accept i + 13j + 8k
\( – 1(0) – 13(1) – 8( – 2) = 3\) (M1)
\( \Rightarrow – x – 13y – 8z = 3\) or equivalent A1
[4 marks]
(i) \((\cos \theta = )\frac{{\left( \begin{array}{c}k\\1\\ – 1\end{array} \right) \bullet \left( \begin{array}{l}1\\1\\0\end{array} \right)}}{{\sqrt {{k^2} + 1 + 1} \times \sqrt {1 + 1} }}\) M1
Note: Award M1 for an attempt to use angle between two vectors formula.
\(\frac{{\sqrt 3 }}{2} = \frac{{k + 1}}{{\sqrt {2({k^2} + 2)} }}\) A1
obtaining the quadratic equation
\(4{(k + 1)^2} = 6({k^2} + 2)\) M1
\({k^2} – 4k + 4 = 0\)
\({(k – 2)^2} = 0\)
\(k = 2\) A1
Note: Award M1A0M1A0 if \(\cos 60^\circ \) is used \((k = 0{\text{ or }}k = – 4)\).
(ii) \(r = \left( \begin{array}{l}3\\0\\1\end{array} \right) + \lambda \left( \begin{array}{c}2\\1\\ – 1\end{array} \right)\)
substituting into the equation of the plane \({\Pi _2}\):
\(3 + 2\lambda + \lambda = 12\) M1
\(\lambda = 3\) A1
point P has the coordinates:
(9, 3, –2) A1
Notes: Accept 9i + 3j – 2k and \(\left( \begin{array}{l}9\\3\\- 2\end{array} \right)\).
Do not allow FT if two values found for k.
[7 marks]
Question
Please revisit the exercises on paragraph HL 1.6 SIMULTANEOUS EQUATIONS. Complete the table below. In case of infinitely many solutions write down the vector equation of the line of intersection
HL 1.6 Exercise | Geometric relationship of the three planes (vector equation of the line of intersection if applicable) |
| 1 | The intersection point of the three planes is \((1,-1,2)\) |
| 2 | |
| 3 | |
| 4 | The three planes intersect in the straight line: |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | If \(k \neq 3, \frac{1}{3}\): If \(k=\frac{1}{3}\): If \(k=3\): |
| 10 |
▶️Answer/Explanation
Ans:
HL 1.6 Exercise | Geometric relationship of the three planes (vector equation of the line of intersection if applicable) |
| 1 | The intersection point of the three planes is (1,-1,2) |
| 2 | The intersection point of the three planes is (-1,2,3) |
| 3 | The intersection point of the three planes is (1.2, 0.6, 1.6) |
| 4 | The three planes intersect in the straight line: \(r=\begin{pmatrix} \frac{-1}{12}\\ \frac{-1}{6}\\ 0\end{pmatrix}+\lambda \begin{pmatrix} \frac{-1}{6}\\ \frac{2}{3}\\ 1\end{pmatrix}\) |
| 5 | The three planes intersect in the straight line: \(r= \begin{pmatrix} 4\\ 1\\ 0\end{pmatrix}+\lambda \begin{pmatrix} 3\\ 2\\ 1\end{pmatrix}\) |
| 6 | Two planes meet in a line and the third plane is parallel to that line. (in other words the three planes form a prism) |
| 7 | The three planes intersect in the line: \(r= \begin{pmatrix} 3\\ -1\\ 0\end{pmatrix}+\lambda \begin{pmatrix} 3\\ -3\\ 1\end{pmatrix}\) |
| 8 | The three planes intersect in the line: \(r=\begin{pmatrix} \frac{11}{3}\\ \frac{-4}{3}\\ 0\end{pmatrix}+\lambda \begin{pmatrix} \frac{-7}{3}\\ \frac{2}{3}\\ 1\end{pmatrix}\) |
| 9 | If \(k \neq 3, \frac{1}{3}\): the three planes intersect in a unique point If \(k=\frac{1}{3}\): the three planes do not intersect (they form a prism) If \(k=3\): the three planes intersect in the line \(r= \begin{pmatrix} -6\\ 3\\ 0\end{pmatrix}+\lambda \begin{pmatrix} -7\\ 2\\ 1\end{pmatrix}\) |
| 10 | When \(a = –1\), the three planes intersect in a unique point. When \(a \neq –1\), the three planes do not intersect in any point (in fact, the two planes intersect in a line and the third plane is parallel to that line, i.e. they form a prism) |
